Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про паралельні та розподілені обчисленняСодержание книги
Поиск на нашем сайте Зміст
ВСТУП Для розв’язання багатьох задач (прогноз погоди, задачі гідро- і газодинаміки, квантової хімії, астрономії, спектроскопії, біології, ядерної фізики) необхідна висока продуктивність та висока швидкість передачі інформації по каналах зв’язку, великі об’єми оперативної і постійної пам’яті, які не можуть забезпечити типові обчислювальні засоби. Одним з шляхів забезпечення таких вимог є організація паралельних та розподілених обчислень і відповідних технічних засобів їх реалізації. Причому, ефективність паралельної обробки залежить як від продуктивності комп’ютерів, так і від розмірів і структури пам’яті, пропускної здатності каналів зв’язку, використаних мов програмування, компіляторів, операційних систем, чисельних методів та інших математичних досліджень. Такий широкий обсяг параметрів вимагає проведення досліджень на різних рівнях: на рівні розпаралелення алгоритмів, створення спеціальних мов програмування, компіляторів, багатопроцесорних систем, неоднорідних систем, кластерів і систем, що розподілені на великих територіях. Великий спектр задач не дозволяє охопити в навчальному посібнику всі проблеми організації паралельних та розподілених обчислень. Для тих, хто хоче краще орієнтуватися в перспективних напрямках розвитку обчислювальної техніки і краще розуміти специфіку паралельних та розподілених обчислень радимо, насамперед, скористатись матеріалами сайту www.parallel.ru Метою вивчення дисципліни є засвоєння основних методів та алгоритмів організації паралельних та розподілених обчислень, принципів побудови відповідних структур, набуття початкових практичних навиків проектування таких засобів. В результаті вивчення курсу студент повинен знати основні методи, алгоритми і засоби паралельної та розподіленої обробки інформації, засоби програмування на паралельних та розподілених структурах, склад апаратних засобів та програмного забезпечення обчислювальних систем з елементами паралельної та розподіленої обробки і класи мов програмування високого рівня для них; вміти виконувати елементарні вправи з розпаралелення задач та алгоритмів, проводити розрахунки параметрів процесорів, проектувати окремі вузли. В розділі курсу “ Організація паралельних обчислень ” розглядаються такі основні питання: - основні поняття про паралельні обчислення; - методи оцінки продуктивності паралельних алгоритмів; - організація мереж Петрі; - розробка паралельного алгоритму; - структури зв’язку між процесорами; - основні класи паралельних комп’ютерів; - схеми паралельних алгоритмів задач; - мови паралельного програмування.
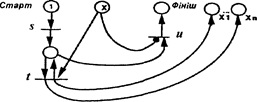
Тема №1: Основні поняття про паралельні обчислення Питання: Конвеєризація і паралелізм Рівні розпаралелення Паралельні операції Конвеєризація і паралелізм Конвеєризація – метод, що забезпечує сукупність різних дій за рахунок їх розбиття на підфункції з зміщенням в часі виконанням. Конвеєрний пристрій розробляють з окремих ступенів, час спрацювання яких в ідеальному випадку повинен бути однаковим. Паралелізм – метод, що забезпечує виконання різних функцій шляхом їх розбиття на підфункції з одночасним виконанням в часі. Приклад: Варіант структурної схем виконання виразу
Рівні розпаралелювання Класифікація паралельності за рівнями, що відрізняються показниками абстрактності розпаралелення задач наведена в табл.1.1. Чим "нижчий" рівень паралельності, тим детальнішим, малоелементнішим буде розпаралелення, що торкається елементів програми (інструкція, елементи інструкції тощо). Таблиця 1.1 Рівні паралельності
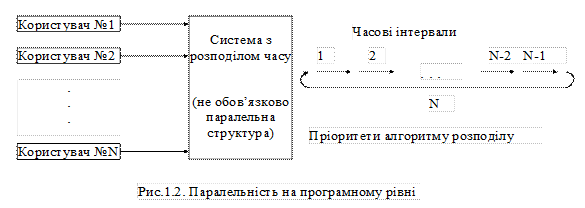
Методи i конструктиви даного рівня обмежуються тільки цим рівнем i не можуть бути поширені на інші рівні. Програмний рівень На цьому рівні одночасно (або щонайменше з часовим розподілом) виконуються комплексні програми (рис.1.2). Комп’ютер, що виконує ці програми не обов’язково повинен мати паралельну структуру, достатньо, щоб на ньому була встановлена багатозадачна операційна система (наприклад, реалізована як система розподілу часу). В цій системі кожному користувачеві, відповідно до його пріоритету, планувальник (Scheduler} виділяє відрізок часу різної тривалості. Користувач одержує ресурси центрального процесорного блоку тільки впродовж короткого часу, а потім стає в чергу на обслуговування. У тому випадку, коли в системі недостатня кількість процесорів для всіх користувачів (або процесів), що, як правило, найбільш імовірно, в системі моделюється паралельне обслуговування користувачів за допомогою "квазіпаралельних" процесів.
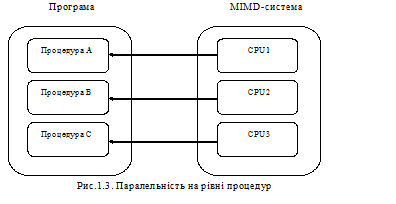
Рівень процедур На цьому рівні різні частини ("процеси") однієї і тієї ж програми виконуються паралельно; кількість операцій обміну даними між процесами повинна бути мінмальною. Основне застосування процедурного рівня розпаралелення - загальне паралельне оброблення інформації, де застосовується ділення вирішуваної проблеми на паралельні задачі - частини, які вирішуються багатьма процесорами з метою підвищення обчислювальної продуктивності (приклад - рис.1.3.).
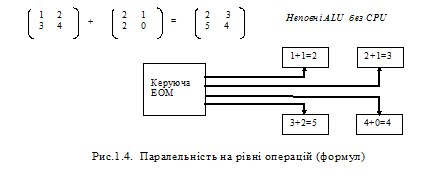
Рівень формул (арифметичних виразів) Арифметичні вирази виконуються паралельно покомпонентно, причому в суттєво простіших синхронних методах. Якщо, наприклад, йдеться про додавання матриць (рис.1.4.), то операція синхронно розпаралелюється просто тому, що на кожному процесорові обчислюється один (чи кілька) елемент матриці. При застосуванні n*n процесорних елементів можна одержати суму двох матриць розмірністю n*n за час виконання однієї операції додавання (за винятком часу, потрібного на виконання операцій читання та запису даних). Цьому рівню притаманні засоби векторизації так званої паралельності даних. Майже кожному елементу даних тут підпорядковується свій процесор, завдяки чому ті дані, що в машині фон Ноймана були пасивними. перетворюються на “активні обчислювальні пристрої”.
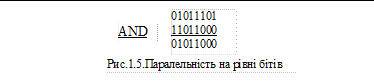
Біт – рівень На цьому piвні відбувається паралельне виконання бітових операцій в межах одного інформаційного слова (рис.1.5). Паралельність на рівні бітів можна знайти в будь-якому працюючому мікропроцесорі. Наприклад, у 8-розрядному арифметико-логічному пристрої побітова обробка виконується паралельними апаратними засобами.
Паралельні операції Інший вид паралельності виникає з аналізу математичних операцій над окремими елементами даних або над групами даних. Розрізняють скалярні дані, операції над якими виконуються послідовно, i векторні дані, операції над якими виконуються паралельно. Прості операції над векторами, наприклад додавання двох векторів, можуть виконуватись синхронно i паралельно. У цьому випадку кожному елементу вектора підпорядковується один процесор. При складніших операціях, таких як формування часткових сум, побудова ефективного паралельного алгоритму є складнішою. Розрізняють одномісцеві (монадні) та двомісцеві (діадні) операції, характерні приклади для яких наведено нижче. Одномісцеві операції а). Скаляр –> скаляр Послідовне виконання Приклад 9‑>3 "Корінь" б). Скаляр ‑> вектор Розмноження числової величини Приклад 9‑>(9,9,9,9) "Broadcast" в). Вектор ‑> скаляр Редукція вектора в скаляр Приклад (1,2,3,4)‑>10 "Складання" (із припущенням, що довжина вектора не змінюється) г-1) Локальна векторна покомпонентна операція. Приклад: (1,4,9,16) ‑> (1,2,3,4) "Корінь" г-2) Глобальна векторна операція з перестановками. Приклад: (1,2,3,4) ‑> (2,4,3,1) "Заміна місць компонент вектора" г-3) Глобальна векторна операція (часто складається з простих операцій) Приклад: (1,2,3,4) ‑> (1,3,6,10) "Часткові суми" Двомісцеві операції д) (скаляр, скаляр)‑> вектор Послідовне виконання Приклад: (1,2)‑>3 "Скалярне додавання" е) (скаляр, вектор)‑>вектор Покомпонентне застосування операцій над скаляром i вектором Приклад: (3,(1,2,3,4))‑>(4,5,6,7) "Додавання скаляра з вектором" Операція виконується як послідовність операцій б) та є) додавання векторів: (3,3,3,3) + (1,2,3,4) (4,5,6,7) є ) (вектор, вектор) ‑> вектор Покомпонентне застосування операції над двома векторами Приклад: ((1,2,3,4),(0,1,,3,2)) ‑> (1,3,6,6) "Додавання векторів" Масштабність (Scaleup) Оскільки для вимірювання ефективності застосовується та сама програма, то показник f в законі Амдала залишається незмінним. Проте, кожна паралельна програма, незалежно від її величини, має послідовно обробляти деяку постійну мінімальну кількість f своїх інструкцій. Це означає, що графіки, які наведені на рис.2.1 і рис. 2.2 із зміною розмірів проблеми стають недійсними! Практичні заміри на паралельних системах з дуже великою кількістю процесорів показали: чим більшими є вирішувана проблема і кількість використовуваних процесорів, тим меншою стає відсоток послідовної частини обчислень. Це дає підставу зробити висновок, що на паралельній системі з дуже великою кількістю процесорів можна досягти високої ефективності. Повний час виконання паралельного алгоритму tp є сумою часу, що витрачається на обчислення tcomp, і часу, що витрачається на комунікації (обмін даними між процесорами) tcomm. Час обчислень оцінюється як час для послідовного алгоритму. tp=tcomp+tcomm. Позначимо час запуску (startup), що інколи називають часом скритого стану повідомлень (message latency), як tstartup. Як початкову апроксимацію часу комунікації візьмемо: tcomm=tstartup+n * tdata. Будемо рахувати tstartup постійним і залежним як від обладнання, так і від програмного забезпечення. Час передачі одного слова даних tdata також вважатимемо постійним. Нехай від одного до другого процесора передаються n даних, тоді теоретичний час комунікацій можна представити в виді графіка (див.рис.2.3).
Висновки Усі без винятку дані, що характеризують продуктивність паралельних обчислювальних систем, мають розглядатися критично. Для цього є цілий ряд причин. 1. Характеристики продуктивності, як показник прискорення і показник масштабності завжди пов'язані з конкретним застосуванням паралельних систем - показники справедливі тільки для даного класу задач і дуже умовно можуть бути поширені на інші задач. 2. Показник прискорення деякої програми стосується тільки одного окремого процесора паралельної системи. 3. В SIMD- системах процесорні елементи, як правило, мають значно меншу потужність в порівнянні з MIMD-процесорами, що може дати на порядок, а то й більше, різницю в оцінках швидкості. 4. Завантаження паралельних процесорів - головна складність в MIMD-системах. У SIMD-системах це не так важливо, бо неактивні процесори не можуть бути використані іншими задачами. Незважаючи на це, показник прискорення обчислюється залежно від характеристик завантаження. Якщо SIMD-програма спробує "включити в роботу" непотрібні ПЕ, то дані завантаження, а з ними і показники прискорення, стануть недійсними. Паралельна програма в цьому випадку буде менш ефективною, ніж за результатами тестування. 5. Порівнюючи паралельну систему (наприклад, векторну) з послідовною (скалярною), не доцільно застосовувати два рази один і той же алгоритм (в паралельній і в послідовній версіях). Приклад. OETS- алгоритм - типовий алгоритм сортування для SIMD-систем, але для послідовних процесорів найефективнішим є алгоритм Quicksort - в усякому разі Quicksort не може бути так просто переведений в ефективну паралельну програму для SIMD-систем. Порівняння “OETS- паралельного” і “OETS- послідовного” алгоритмів дає хороші результати для паралельної системи, але воно не має практичного глузду!
Поняття про мережі Петрі Прості мережі Петрі Розширені мережі Петрі Поняття про мережі Петрі Мережі Петрі призначені для представлення координації асинхронних подій і застосовуються для описування взаємовідносин між паралельними процесами та їх синхронізацією. Мережа Петрі - це орієнтований, дводольний граф з мітками (марками). Це визначення треба розуміти так (рис.3.1):
На рис.3.2 показано просту мережу Петрі, що має один перехід, три ребра i три вузли, два з яких марковані i один не маркований. Кожен вузол зв'язаний з переходом за допомогою одного ребра.
Прості мережі Петрі Визначення: Активізація (Стан): перехід t активізований, якщо всі вхідні вузли pi цього переходу марковані. Тобто, активізація - це залежна від часу властивість переходу i описує деякий стан. Перехід мережі Петрі на рис.3.2 активізований, бо обидва вузли ребер, що входять у перехід, марковані. Ввімкнення (Подія): активізований перехід t може вмикатися. Тоді зникають марки з вcix вхідних вузлів pi переходу t i маркуються всі вихідні вузли pj цього переходу. Процес увімкнення переходу має передумовою його активізацію. Як видно з рис.3.3, в процесі ввімкнення відбувається зміна маркування вузлів мережі Петрі: перехід активізований, бо обидва вузли вхідних ребер марковані. Після ввімкнення переходу маркування обох верхніх (вхідних) вузлів зникає, в той час як на нижньому (вихідному) вузлі з'являється нова марка. Загальна кількість маркувань у будь-якій мережі Петрі не залишається постійною. Якби на вихідному вузлі вже була марка, то вона б переписалася, тобто вузол як i раніше був би зайнятий маркою.
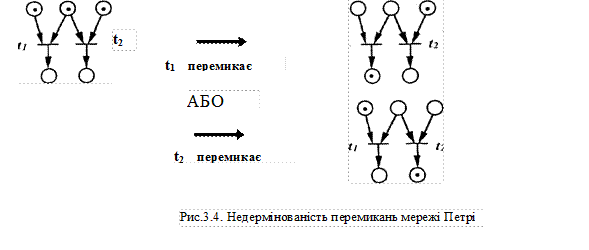
Невизначеність: якщо одночасно активізовані декілька переходів, то не зрозуміло, який з них перемкнеться першим. Зроблені вище визначення не дають уявлення про порядок перемикання декількох активізованих переходів. Одночасне перемикання їх неможливе! Як показано на рис.3.4, у цьому випадку можуть відбуватися два процеси i який з них фактично має місце, в мережі Петрі визначити не можна. У зв'язку з тим, що ввімкнення одного або іншого переходу не може бути здійснене за допомогою зовнішніх параметрів, мережа Петрі має в цьому випадку невизначеність. Стан: стан маркування (або, коротко, стан) мережі Петрі до деякого моменту часу Т визначено як сукупність маркувань кожного окремого вузла мережі.
У простих мережах Петрі стан маркування можна відобразити за допомогою деякої послідовності бінарних цифр (двійковий рядок). Можливе перемикання переходу задається за допомогою переходу в послідовність стану (якщо за аналогією з показаним на рис.3.4 можуть перемикатися декілька переходів, то існують різноманітні можливі послідовності станів):
У тому випадку, коли перемикання кожного переходу визначається цим правилом, всі послідовності станів одного заданого початкового стану можуть бути “обчислені” комп'ютером i можуть бути розпізнані вірогідні блокування. Генерування марок: перехід, що не має жодного вхідного ребра, завжди активізований i може постійно видавати нові марки на вихідні вузли, що з’єднані з ним. Знищення марок: перехід, що не має жодного вихідного ребра i має тільки одне вхідне ребро, завжди активізований тоді, коли це місце марковано i він може постійно знищувати марку. “Мертвий" стан: Мережа Петрі перебуває в "мертвому" стані (блокована), якщо жоден з переходів не активізований.
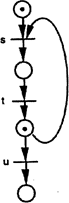
Блокована мережа Петрі є статичною, тобто в ній немає нових послідовностей станів. Наприклад, обидві мережі Петрі, що показані на рис.3.4, блоковані. “Живий” стан: мережа Петрі перебуває в "живому" стані (не блокована в жодному моменті часу), якщо хоча б один з її переходів активізований i це справедливо також для кожного наступного стану. Зауважимо, що "живий" стан не є протилежністю "мертвого" стану. Мережа Петрі в "живому" стані не блокована i не перебуває в жодному із можливих послідовностей станів, в той час як не блокована мережа Петрі не обов'язково має бути в "живому" стані. Наприклад, блокування може відбутися тільки після багатьох послідовних кроків. На рис. 3.6 показано два приклади мереж. Ліва мережа Петрі (рис.3.6) є "живою" тому, що її маркування змінюється від одного вузла до іншого, але не зникає; перехід завжди тут активізований. В правій мережі Петрі можуть перемикатись або перехід и (i тоді мережа негайно переходить у "мертвий" стан), або перехід s. Нарешті можуть перемикатись один раз переходи t i U, що веде також до "мертвого" стану мережі Петрі. За допомогою мереж Петрі можна уникнути взаємоблокування процесів або виникнення суперечних даних у тих випадках, коли два процеси мають звернутися до однієї і тієї області даних (рис.3.7).
Рис. 3.6. Діюча та блокуюча мережі Петрі
Процес P1 (виробник) генерує тут незалежно від процесу P2 дані, записує їх у буферну область пам'яті i хоче без затримки працювати далі. Процес P2 (споживач) читає дані із цього буфера i використовує їх паралельно з процесом P1. Щоб уникнути суперечливих даних треба виконати таку умову: одночасний доступ процесів в одну і ту саму область пам'яті має бути виключений. Це викликає потребу в синхронізації процесів, тобто один з них має деякий час почекати. На рис.3.8 показано простий приклад для випадку, коли процеси P1 та P2 мають бути синхронізовані, тому, що вони, наприклад, хочуть користуватися одними і тими самими даними.
P1 - семафор Рис. 3.8. Мережа Петрі для синхронізації процесів Кожний процес має тут два стани - активний i пасивний, які символізуються двома вузлами. Процес перебуває в тому стані, який позначається відповідною маркою (на рис.3.8 обидва процеси пасивні). Кожен з двох процесів може змінювати свій стан з пасивного на активний i навпаки, перемикаючи відповідний перехід. Обидва цикли стану для P1 i P2 аналогічні простому контуру, що зображений зліва на рис.3.6, але ці цикли пов'язані між собою за допомогою семафора S. Процес, що хотів би змінити свій стан з пасивного на активний (щоб звернутися до загальних даних), потребує для цього переходу маркування в S. Це означає, що він тільки тоді може змінити свій стан на активний, коли марка семафора не використовується іншим процесом (який в цей час перебуває в активному стані). При переході в активний стан семафор S звільняється від маркування; у тому випадку, коли інший процес запросить перехід з пасивного стану в активний (доступ до загальних даних), він має чекати, поки перший процес не перейде знову зі стану активного в пасивний i знову з'явиться семафор-марка S. Синхронізація за допомогою цієї мережі Петрі є високонадійною, оскільки, в кожний момент часу тільки один процес перебуває в активному стані. Таким чином, в разі одночасного запиту процеси з паралельних перетворюються в послідовні i їх блокування виникнути не зможе. Розширені мережі Петрі За допомогою трьох простих розширень прості мережі Петрі стають суттєво продуктивнішими.Як показано Хопкрофтом i Ульманом, "розширені мережі Петрі” (навіть без додатково введених нижче ваг дуг) за своєю ефективністю рівні машині Тьюрінга, тобто вони можуть застосовуватись як загальна модель обчислюваності. Розширення: Багаторазове маркування.
- перехід активізований тільки тоді, коли число, що відповідає кількості маркувань кожного його вхідного вузла, є більшим чи дорівнює одиниці; - якщо активізований перехід перемикається, то числа-маркування ycix вхідних вузлів цього переходу зменшуються, а ycix вихідних вузлів - збільшуються на одиницю. Тобто кількість маркувань одного вузла може бути як завгодно великою, але відповідне число не може бути меншим від нуля. Дуги-заперечення Дуги-заперечення в мережах Петрі зображаються кружечком на кінці замість стрілки (рис.3.9) i не мають дугової ваги; дуги, що були визначені раніше, розглядаються як позитивні.
Рис. 3.9. Дуга-заперечення Вони завжди направлені тільки від деякого вузла до деякого переходу, зворотного напрямку не дозволяється. Введення дуг-заперечень зумовлює оновлені пристосування правил активізації та перемикань: - перехід активізований тільки тоді, коли кількість маркувань кожного вхідного вузла з позитивною дугою більша або дорівнює одиниці i коли кількість маркувань кожного вхідного вузла з дугою-запереченням дорівнює нулю (на рис.3.9 перехід t активізований, якщо P1 маркований i P2 не маркований); - якщо активізований перехід перемикається, то кількість маркувань ycix вхідних вузлів з позитивними дугами цього переходу зменшується на одиницю, в той час як кількість маркувань вхідних вузлів з дугами-запереченнями залишається незмінною. Числа, що відповідають кількості маркувань ycix вихідних вузлів, як i раніше, збільшуються на одиницю. Вага дуг Кожна дуга, що не є дугою-запереченням, може мати постійну цілочислову вагу, що більша або дорівнює одиниці (число, що використовується за замовчанням, рис. 3.10). Для активізації i перемикання переходу діє правило: - перехід активізований тільки тоді, коли кількість маркувань кожного його вхідного вузла більша або дорівнює відповідній вазі дуги, а для дуги-заперечення дорівнюють нулю; - при перемиканні переходу кількість маркувань кожного вхідного вузла зменшується на вагу відповідної вхідної дуги (вона залишається незмінною для дуг-заперечень); кількість маркувань кожного вихідного вузла збільшується на вагу відповідної вихідної дуги.
Пам’ять Z:=Z+X*Y Рис. 3.13. Мережа Петрі для операції множення Новий обчислювальний цикл починається, якщо "пам'ять" дорівнює нулю; потім перехід знову активізується через дугу заперечення. Цикли, в яких величина Y додається з Z, виконуються доти, поки Х стане дорівнювати нулю, тобто добуток X*Y буде додано з Z. На рис.3.14 показано можливість розмноження значень змінної величини. На рис.3.15, 3.16 наведено приклади складних мереж Петрі, як скомпоновані з простіших модулів за методом чорного ящика.
Рис. 3.14. Розмноження значень змінної Х Послідовні обчислення
Старт Фініш
Рис. 3.15. Послідовне використання мережі Петрі
Паралельні обчислення
Рис. 3.16. Паралельне використання мережі Петрі Паралелізм даних Паралелізм задач Паралелізм даних Паралелізм даних базується на застосуванні однієї операції до кількох елементів масиву даних і може використовуватися при векторній і паралельній обробці. Основними ознаками підходу є: - обробкою даних керує одна програма; - простір є глобальним (для програміста є одна єдина пам’ять, а деталі структури даних доступні до пам’яті і міжпроцесорного обміну для програміста скриті); - слабка синхронізація обчислень на паралельних процесорах (кожен процесор виконує один той же фрагмент програми, але нема гарантії, що в даний момент часу на всіх процесорах виконується одна і таж машинна програма); - паралельні операції над елементами масиву виконується на всіх допустимих даній програмі процесорах. Базовими операціями для даної моделі паралелізму є: операції керування даними, операції над масивами та їх фрагментами, умовні операції, операції приведення, зсуву, сканування, пересилання даних. Для програмування в моделі паралелізму даних використовуються спеціалізовані мови програмування, здебільшого різновидності мови FORTRAN. А сам програміст – слабо впливає на процес і результати роботи Паралелізм задач Метод передбачає розбиття задачі на кілька відносно самостійних підзадач. Найефективніше дана модель реалізовується на MIMD структурі, де кожен процесор виконує свою програму (FORTRAN чи С). Оскільки в даному випадку програмісту самому необхідно контролювати як розподіл даних між процесорами і різними під задачами так і організацію обміну даними між ними, то підхід є більш трудоємкісним від попереднього. При паралелізмі задач виникають певні проблеми: - підвищена трудоємність розробки і відлагодження програм; - на програміста покладається вся відповідальність за збалансоване завантаження програм; - програмісту необхідно мінімізувати обмін даними між процесорами. - підвищена небезпека виникнення тупикових ситуацій. Проте забезпечується висока гнучкість і свобода програмісту у виборі напрямку і особливостей організації паралельної роботи. Крім того, для даної моделі є розроблений великий клас спеціалізованих бібліотек: MPI (Message Passing Interface), PVM (Parallel Virtual Machines). Проектування комунікацій Оскільки підзадачі не можуть бути абсолютно незалежними, наступним етапом розробки паралельного алгоритму є проектування обмінів даними між ними, яке полягає в визначенні структури каналів зв’язку і повідомлень, якими повинні обмінюватися підзадачі. Канали зв’язку можуть програмуватися явно і неявно. Якщо на першому етапі виконувалась декомпозиція даних, тоді проектувати комунікації дуже важко. При функціональній декомпозиції проектування комунікацій простіше – вони відповідають потокам даних між підзадачами. Комунікації класифікуються за такими ознаками: розміщення, структурованості, за відношенням до зміни в часі, за відношенням до засобів синхронізації. За розміщенням комунікації поділяються на: - локальні (кожна підзадача зв’язана з невеликою кількістю інших підзадач); - глобальні (кожна підзадача зв’язана з великою кількістю інших підзадач). За ознакою структурованості комунікації поділяються на: - структуровані (кожна підзадача і підзадачі, що зв’язані з нею утворюють регулярну структуру); - неструктуровані (підзадачі зв’язані довільним графом). За відношенням до зміни в часі комунікації поділяються на: - статичні (схема комунікації з часом не змінюється); - динамічні (схема комунікації змінюється в процесі виконання програми). За відношенням до засобів синхронізації комунікації є: - синхронні (відправник і отримувач даних координують обмін між собою). - асинхронні (обмін даними не координується). Рекомендації з проектування комунікацій: - кількість комунікацій у підзадачах повинна бути приблизно однаковою (в іншому випадку буде погана масштабованість); - ефективніше використовувати локальні комунікації; - комунікації повинні бути паралельними. Крім того, при проектуванні комунікацій необхідно уникати тупикових ситуацій, які можуть бути зв’язані з неправильною послідовністю обміну даними між процесами (Наприклад, перший процес очікує дані від другого, другий від третього, а останньому потрібні результати роботи першого). Обмін повідомленнями може бути реалізований по різному: за допомогою потоків, міжпроцесорних комунікацій, тощо. Найрозповсюдженіший спосіб програмування комунікацій – використання бібліотек, що реалізують обмін повідомленнями, наприклад, бібліотеки PVM i MPI дозволяють створити паралельні програми для різних платформ. CORBA (Common Object Reguest Broker Architecture) визначає протокол взаємодії між процесами, незалежний від мови програмування і операційної системи. Для опису інтерфейсу використовується декларативна мова IDL (Interface Definition Language). Укрупнення На етапі, на відміну від попередніх, враховується архітектура обчислювальної системи. При цьому часто приходиться об’єднувати задачі, які були отримані на попередніх етапах, для того, щоб їх кількість дорівнювала кількості процесорів. Метою укрупнення є збільшення зернистості обчислень і комунікацій, збереження гнучкості і зменшення вартості розробки. Загальні вимоги: - зниження затрат на комуніка
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 при паралельній обробці наведений на рис.1.1.
при паралельній обробці наведений на рис.1.1.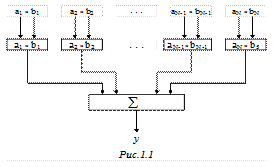


 Кожна мережа Петрі є графом з двома різними групами вершин: вузли та переходи. Між вузлами та переходами можуть міститися орієнтовані ребра (дуги), але два вузли або два переходи не можуть з’єднуватися ребрами. Між кожною парою вузол/перехід може існувати максимально одне ребро від вузла до переходу (ребро входу) i максимально одне ребро від переходу до вузла (ребро виходу). Вузли можуть бути вільними або зайнятими міткою (маркованими); переходи не можуть бути маркованими. Вузли, що є стартовими пунктами одного ребра до одного переходу t, називаються далі вхідними вузлами переходу t. Вузли, що є кінцевими пунктами ребра від переходу t називаються вихідними вузлами переходу t.
Кожна мережа Петрі є графом з двома різними групами вершин: вузли та переходи. Між вузлами та переходами можуть міститися орієнтовані ребра (дуги), але два вузли або два переходи не можуть з’єднуватися ребрами. Між кожною парою вузол/перехід може існувати максимально одне ребро від вузла до переходу (ребро входу) i максимально одне ребро від переходу до вузла (ребро виходу). Вузли можуть бути вільними або зайнятими міткою (маркованими); переходи не можуть бути маркованими. Вузли, що є стартовими пунктами одного ребра до одного переходу t, називаються далі вхідними вузлами переходу t. Вузли, що є кінцевими пунктами ребра від переходу t називаються вихідними вузлами переходу t.





 Не діюча, блокує через декілька кроків
Не діюча, блокує через декілька кроків
 Діюча
Діюча