
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порівняння mimd і simd структур за продуктивністюСодержание книги
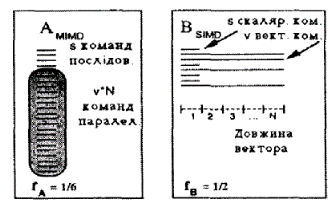
Поиск на нашем сайте Вище, при аналізі продуктивності паралельних обчислювальних систем не розрізнялись MIMD- та SIMD- системи. Проте кожна програма містить у собі як мінімум два різних максимальних показника паралельності: один для асинхронної паралельної обробки, PMIMD, а другий - для синхронної, PSIMD. У зв'язку з універсальністю асинхронної паралельної обробки має місце співвідношення PSIMD £ PMIMD. На практиці необхідно звернути увагу на такі моменти: - якщо в MIMD-системі є вільні процесори, що не використовуються в даній задачі, то вони можуть бути застосовані іншими користувачами для своїх задач, що розв'язуються одночасно. В SIMD-системах неактивізовані процесори не використовуються; - спосіб обробки інформації в SIMD-програмах дає суттєво менші показники розгалуження; - процесорні елементи SIMD- систем, як правило, менш потужні, ніж процесори, що застосовуються в MIMD-системах, але цей недолік компенсується за рахунок значно більшої кількості процесорів SIMD- систем порівняно з MIMD-системами. У MIMD-системах часто програмуються задачі в “SIMD-режимі”, тобто не використовується можлива незалежність окремих процесорів. Особливо це помічається, коли задача, що розв’язується, розподіляється між великою кількістю процесорів, тобто коли мова йде фактично про масивну паралельність. Ця обставина є одним з найвагоміших аргументів на користь SPMD- моделі паралельності (same program, multiply data), яка виникає внаслідок змішаного використання SIMD і MIMD в рамках однієї системи. У зв'язку з тим що за законом Амдала ефективність сильно залежить від кількості процесорів, а з іншого боку, не має можливості уникнути деякої послідовної частини програми (як мінімум, залишаються програми вводу-виводу даних), постає питання: чи доцільно взагалі використовувати паралельну SIMD-систему з кількістю процесорів? Якщо помилково застосувати закон Амдала, то можна одержати неправильні результати, до яких насамперед приводить спосіб обліку інструкцій (рис.2.5). У той час як в програмі А (наприклад, в MIMD- програмі) відповідно до формули Амдала враховується кожна елементарна операція (це дає фактор fA), в програмі В для SIMD-системи як скалярні, так і векторні операції враховуються як одна інструкція (це дає фактор fB). Таке визначення є природним для SIMD-системи, бо кожна операція, що так враховується, потребує приблизно однакового часу на виконання. Отже, маємо: - fA - послідовну частину програми відносно кількості елементарних операцій; - fB - послідовну частину програми відносно тривалості виконання операцій. На рис.2.5 SIMD-програма може працювати паралельно половину свого часу (fB =0,5). Водночас кількість послідовно виконуваних елементарних операцій суттєво менша, а саме fA =1/6. Залежність між цими двома факторами виражається формулою
Для отримання точних даних продуктивності, можна застосувати для кожної SIMD- інструкції виражену у відсотках кількість активних в цій інструкції процесорів відносно їхньої загальної кількості: це буде число між нулем (у випадку виконання скалярної операції в керуючій ЕОМ) та одиницею (випадок, коли всі ПЕ активні).
Рис. 2.5 Оцінка кількості паралельних інструкції Для визначення показника прискорення SIMD-системи можна перерахувати ТN, на T1, відповідно до запитання: "Скільки часу було б потрібно послідовній ЕОМ для виконання цієї паралельної програми?". Визначення: - fB – частина скалярних інструкцій (у відсотках) SIMD-програми відносно загальної кількості (скалярних і векторних) інструкцій. Можна вважати ідентичним і таке визначення - fB: частина часу виконання послідовних операцій (у відсотках) відносно загальної тривалості виконання паралельної програми. Тоді,
Приклади застосування зміненого закону 1. · Система має 1000 процесорів. · Програма має максимальний показник розпаралелення 1000. · • 0,1 % програми (в SIMD-обчисленні) виконується послідовно, тобто f = 1/1000. Обчислення показника прискорення: S1000=0.001+(1-0.001)*1000»999 У цьому випадку досягається прискорення, близьке до теоретично максимально можливого (E1000 =100%). Приблизний результат одержуємо і за формулою Амдала з відповідним fA.
Показник прискорення за формулою Амдала:
2. · Система має 1000 процесорів · Програма має максимальний показник розпаралелювання 1000 · 10% програми (в SIMD-обчисленні) виконується послідовно, тобто fB =0.1. Обчислення показника прискорення: S1000 =0,1+0,9*1000=900. Незважаючи на помітно велику послідовну частину SIMD-програми досягається 90% максимального прискорення! Наведені тут міркування спрямовані на чітко окреслену проблему (з відповідно великим максимальним показником розпаралелення) і на задану незмінну кількість процесорних елементів: ні розміри задачі, ні кількість процесорів не змінюються, проводиться тільки порівняння з послідовною системою. У випадку, коли змінюється кількість ПЕ в процесі виконання програми, оцінити, як змінюється при цьому показник speedup, за наведеною формулою для SN неможливо, бо вона базується на параметрі TN! Збільшення кількості ПЕ не привело б до швидшого виконання тієї самої SIMD-програми в області N > РSIMD (кількість ПЕ - більша або дорівнює максимальному показнику SIMD - розпаралелення), бо ці додаткові ПЕ були б зайвими і залишались би неактивними. Обчисливши всі Ti, де 1<і<N, можна знайти відповідні показники прискорення Si:
Наведена вище формула для SN використана для екстраполяції тривалості виконання масштабованих варіантів проблеми з лінійним масштабним коеффіцієнтом (Skaleup) і визначена як “ scaled speedup ” (показник прискорення, пов'язаний з масштабами задач), що легко вводить в оману: тут досліджувались часові показники різних за масштабами варіантів програми і обчислені показники прискорення відносно цих варіантів. Було також прийнято, що послідовна частина (за формулою Амдала) деякої "реальної" програми при її масштабуванні залишається постійною, а збільшується лише паралельна частина. Проте за визначенням це є клас програм з лінійним показником масштабності (scaleup), тобто для нього справедлива формула
де k - число, яке показує, що в k разів більший варіант програми виконується в k разів більшою кількістю процесорів за той же час. Крім того, завжди виконується умова:
З цього обмеженого класу задач, випливає лінійний приріст показника “ scaled speedup ”:
Висновки Усі без винятку дані, що характеризують продуктивність паралельних обчислювальних систем, мають розглядатися критично. Для цього є цілий ряд причин. 1. Характеристики продуктивності, як показник прискорення і показник масштабності завжди пов'язані з конкретним застосуванням паралельних систем - показники справедливі тільки для даного класу задач і дуже умовно можуть бути поширені на інші задач. 2. Показник прискорення деякої програми стосується тільки одного окремого процесора паралельної системи. 3. В SIMD- системах процесорні елементи, як правило, мають значно меншу потужність в порівнянні з MIMD-процесорами, що може дати на порядок, а то й більше, різницю в оцінках швидкості. 4. Завантаження паралельних процесорів - головна складність в MIMD-системах. У SIMD-системах це не так важливо, бо неактивні процесори не можуть бути використані іншими задачами. Незважаючи на це, показник прискорення обчислюється залежно від характеристик завантаження. Якщо SIMD-програма спробує "включити в роботу" непотрібні ПЕ, то дані завантаження, а з ними і показники прискорення, стануть недійсними. Паралельна програма в цьому випадку буде менш ефективною, ніж за результатами тестування. 5. Порівнюючи паралельну систему (наприклад, векторну) з послідовною (скалярною), не доцільно застосовувати два рази один і той же алгоритм (в паралельній і в послідовній версіях). Приклад. OETS- алгоритм - типовий алгоритм сортування для SIMD-систем, але для послідовних процесорів найефективнішим є алгоритм Quicksort - в усякому разі Quicksort не може бути так просто переведений в ефективну паралельну програму для SIMD-систем. Порівняння “OETS- паралельного” і “OETS- послідовного” алгоритмів дає хороші результати для паралельної системи, але воно не має практичного глузду!
|
||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

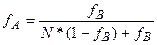 .
.


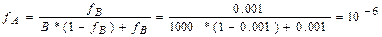 .
.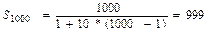 .
. ;
; 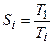
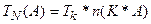
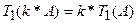 - програма, більша в k разів, потребує при виконанні на одному процесорі в k разів більше часу.
- програма, більша в k разів, потребує при виконанні на одному процесорі в k разів більше часу.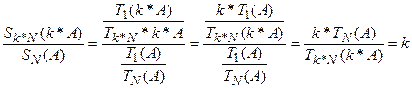 .
.


