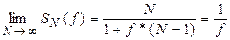Характеристики продуктивності паралельних алгоритмів.

Характеристиками продуктивності паралельних алгоритмів є: фактор прискорення, максимальне прискорення (закон Амдала), ефективність паралельного алгоритму, ціна, масштабність, загальний час виконання паралельного алгоритму, повний час виконання паралельного алгоритму, теоретичний час комунікацій.

Оцінюючи продуктивність безпосередньо на паралельних системах, відзначають позитивний ефект від розпаралелювання (Speedup - прискорення) і вигоди від збільшення масштабності розв'язаних задач (Scaleup).

Показник Speedup визначає, у скільки разів швидше може бути вирішена одна й та ж задача на N процесорах порівняно з її вирішенням на одному процесорі.

Показник Scaleup визначає, у скільки разів більшу за розмірами проблему можна вирішити за той же час N процесорами порівняно з проблемою, що вирішується одним процесором.

Амдалом сформульований "закон Амдала", де єдиним параметром є поділ програми на послідовну і паралельну частини; масштаб вирішуваної задачі залишається постійним. Розгляньмо дещо спрощену формулу цього закону.

Фактор прискорення. Прискоренням (speedup factor) паралельного алгоритму в N – процесорній системі називається величина S(N) = Т₁/Т_N, де

- Т₁ – час виконання алгоритму на одному процесорі чи однопроцесорній системі;

- Т_N – час виконання алгоритму на багатопроцесорній системі з N - процесорами.

Закон Амдала. Позначимо:

- Р_с - максимальний ступінь розпаралелення (максимальна кількість процесорів, які можуть працювати паралельно в будь-який момент часу в період виконання програми). Тут вирішальне значення має також тип застосовуваної моделі паралельності (наприклад, MIMD чи SIMD);

- T_k - тривалість виконання програм з максимальним показником розпаралелення на системі з k процесорами;

- N - кількість процесорів у паралельній системі;

- f – відсоток послідовних операцій програми (не можуть бути виконані паралельно на N процесорах).

Тривалість виконання програми на паралельній системі з N процесорами оцінюється формулою:

,

звідки дістанемо показник прискорення (Speedup) в системі з N процесорами

.

Оскільки, 0< f < 1, справедливе таке співвідношення:

,

тобто показник прискорення не може бути більшим ніж кількість процесорів N.

Як міра досягнутого прискорення, відносно максимального визначається ефективність системи з N процесорами

Область межі ефективності:

На практиці використовують значення у відсотках. При = 0,9. наприклад, могла б бути досягнута ефективність, що дорівнює 90% максимально можливої.

Приклади застосування закону Амдала

1. Система має N=1000 процесорів

• Програма має максимальний показник розпаралелення 1000

• 0,1% програми виконується послідовно (наприклад, операції вводу-виводу), тобто f=0,001 Обчислення показника прискорення дають:

8

Таким чином, незважаючи на суттєво малу долю послідовної частину програми, у цьому випадку досягається тільки половина максимально можливого прискорення, тобто Ефективність буде .

2. Система має N=1000 процесорів

• Програма має максимальний показник розпаралелення 1000.

• 1% програми має виконуватися послідовно, тобто f=0,01

Показник прискорення:

Ефективність E₁₀₀₀ = 9,1%. тобто використовується тільки 9,1% загальної потужності процесорів і це при малій, на перший погляд, послідовній частині програми!

З збільшенням послідовної частини програми падає завантаження процесорів, а з ним і показник прискорення порівняно з послідовною обчислювальною системою. Для кожної послідовної частини програми може бути обчислений максимально можливий показник прискорення незалежно від кількості застосовуваних процесорів:

Це означає, що програма із скалярною частиною, яка становить 1%, ніколи не зможе досягти показника прискорення (Speedup), що був би більшим 100 - незалежно від того, застосовується 100,1000 або 1000000 процесорів.

На рис.2.1 наведені графіки залежності показника прискорення від кількості процесорів N для різних величин послідовної частини програми f. Головна діагональ належить до лінійного прискорення і може бути побудована при f=0.

Рис. 2.1. Залежність прискорення від кількості процесорів

 

На рис. 2.2 наведені графіки залежності ефективності від N і f.

Рис. 2.2. Залежність ефективності від кількості процесорів.

Ефективність паралельного алгоритму Е показує у скільки разів більший час виконання завдання одним процесором Т₁, ніж час виконання цього ж завдання багатопроцесорною системою Т_N, помножений на кількість процесорів N. Е = Т₁/(Т_N*N) = S_N/ N. Ефективність характеризує ту частину часу, яку процесори використовують на обчислення.

Ціна (робота) обчислення визначається як Cost = (час виконання) * (повне число використаних процесорів). Ціна послідовних обчислень рівна часу їх виконання Т_{1 .} Ціна паралельних обчислень рівна Т_N*N. З іншого боку Т_N = Т₁/S_{N .} Звідси ціна паралельних обчислень: Cost = Т₁*N/ S_N = Т₁/ Е. Цінооптимальні паралельні алгоритми – алгоритми, в яких ціна для вирішення проблеми на багатопроцесорній системі є пропорційною ціні (часу виконання) на однопроцесорній системі.

Масштабність (Scaleup)

Оскільки для вимірювання ефективності застосовується та сама програма, то показник f в законі Амдала залишається незмінним. Проте, кожна паралельна програма, незалежно від її величини, має послідовно обробляти деяку постійну мінімальну кількість f своїх інструкцій. Це означає, що графіки, які наведені на рис.2.1 і рис. 2.2 із зміною розмірів проблеми стають недійсними! Практичні заміри на паралельних системах з дуже великою кількістю процесорів показали: чим більшими є вирішувана проблема і кількість використовуваних процесорів, тим меншою стає відсоток послідовної частини обчислень. Це дає підставу зробити висновок, що на паралельній системі з дуже великою кількістю процесорів можна досягти високої ефективності.

Повний час виконання паралельного алгоритму t_p є сумою часу, що витрачається на обчислення t_comp, і часу, що витрачається на комунікації (обмін даними між процесорами) t_comm. Час обчислень оцінюється як час для послідовного алгоритму. t_p=t_comp+t_comm. Позначимо час запуску (startup), що інколи називають часом скритого стану повідомлень (message latency), як t_startup. Як початкову апроксимацію часу комунікації візьмемо: t_comm=t_startup+n * t_data. Будемо рахувати t_startup постійним і залежним як від обладнання, так і від програмного забезпечення. Час передачі одного слова даних t_data також вважатимемо постійним. Нехай від одного до другого процесора передаються n даних, тоді теоретичний час комунікацій можна представити в виді графіка (див.рис.2.3).

Для передачі q повідомлень, кожне з яких має довжину n-даних, необхідний час t_comm=q(t_startup+n t_data). Інформативною величиною є також відношення обчислювальних затрат до комунікаційних: t_comp/t_comm.