
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вправи і завдання до теми №4Содержание книги
Поиск на нашем сайте 1. Дайте порівняльну характеристику моделям паралелізму даних і паралелізму задач. 2. Розробіть структуру паралельного алгоритму виконання функції 3. Як переваги забезпечує використання збалансованого завантаження процесорів? 4. На якому етапі розробки паралельного алгоритму необхідно враховувати параметри процесорів? 5. Чи завжди на етапі укрупнення головною вимогою є “Зниження затрат на комунікації”?
Тема №5: Структури зв’язку між процесорами Питання: Основні положення Шинні мережі Сітки з комутаторами Структури, що забезпечують зв’язок типу «пункт-пункт» Методи комутацій Вправи і завдання до теми №5
Основні положення Кожна паралельна система/процесор складається з ряду процесорів і модулів пам'яті, які зв'язані через відповідні комутаційні структури. Bci концепції комунікацій, такі як "schared memory" (загальна пам'ять, реальна або віртуальна), або обмін повідомленнями реалізуються в паралельних системах деякими наявними структурами. Враховуючи задачі обчислювальної системи, її структура зв'язку має відповідати різним критеріям, насамперед, забезпечувати по можливості високу коннективність (гарантувати зв'язок між двома будь-якими процесорами або модулями пам'яті без потреби переходу через проміжні пункти комутації). Окpiм цього, має забезпечуватись найбільша кількість одночасних зв'язків, - щоб комутаційна мережа не обмежувала продуктивність вузлів паралельної обробки інформації. Проте об'єктивно існують різноманітні обмеження на реалізацію цих критеріїв: кількість ліній зв'язку на один процесор не може збільшуватися безмежно, має також фізичні обмеження i ширина частотної смуги пропускання (швидкість передачі) комутаційної мережі. Для паралельної системи, яка складається з процесорних елементів (ПЕ) можна визначити такі види витрат: - кількість зв'язків на один ПЕ (витрати на виготовлення системи); - дистанція між ПЕ (витрати під час експлуатації). Тобто, кількість зв'язків на один процесор i дистанція, тобто найкоротший шлях між двома заданими ПЕ, мають бути якомога меншими. Структура зв'язку має бути розширюваною за масштабом, тобто малі мережі зв'язку мають збільшуватися завдяки доповненням. Структури зв'язку поділяються на три великих класи: - шинні сітки; - сітки з комутаторами; - структури, що забезпечують зв'язок типу "пункт-пункт". Причому, для всіх цих структур основною характеристикою мережі залишається пропускна здатність, одиницею вимірювання якої є біт/с. Наведемо основні визначення, які відносяться до структури зв’язків. Топологія – організація внутрішніх комунікацій обчислювальної системи. Два вузли є сусідніми, якщо між ними є прямі з’єднання. Порядком вузла називається кількість його сусідів (позначається V – кількість зв’язків). Комунікаційним діаметром мережі є мінімальний шлях між двома сусідніми вузлами (позначається А – віддаль). Масштабованість характеризує зростання складності з’єднань при добавленні в конфігурацію нових вузлів. (При довільній масштабованості системи, її складність при нарощуванні буде незначно змінюватись, незмінним буде діаметр мережі) Є два типи технології комутації мереж – статичні і динамічні. Шинні мережі В паралельних структурах засобами шини можна з'єднати між собою процесори або модулі пам'яті (рис.5.1).
Рис. 5.1. Шинна система Кількість зв'язків на один ПЕ є оптимальною, віддаль мiж ПЕ є незмінною i дорівнює 2 (кожний зв'язок йде від ПЕ до шини i назад). Це також практично оптимально число. Недоліки шинної організації зумовлені тим, що в кожний момент може відбуватись тільки одне з'єднання. Паралельне читання за однією і тією адресою вузла пам'яті можливе, однак запис - нi. Процесори не можуть незалежно обмінюватися даними; паралельна обробка при обміні даними між процесорами неможлива. Система керування шиною має гарантувати послідовне упорядкування одночасних запитів на послуги шини. Якщо система може розширюватися на багато процесорів, то ширина частотної смуги пропускання шини залишається незмінною. Цей важливий недолік визначає масштабні спроможності шинних структур. Тому шинні системи як засоби зв'язку в паралельних ЕОМ, в яких кількість процесорів перевищує десять, застосовувати не рекомендується. Мережі з комутаторами Сітки з комутаторами - це динамічні структури зв'язку, в яких за допомогою ліній керування реалізовані різні варіанти спілкування процесорів перед початком виконання паралельної програми. Розглянемо динамічні сітки типів: розподілювача перехресних шин, дельта-сітки, мережі зв'язку Клоса та сітки типу Fat-Tree. На рис.5.2 наведена схема розподілювача перехресних шин. Кожний ПЕ має n-1 пункт комутації, оскільки діагональні пункти не потребують контакту. Загалом сітка має n(n-1) пунктів комутації i дає можливість встановити будь-яку кількість з'єднань між всімаПЕ, тобто без всяких колізій може відбуватись повністю паралельний обмін даними. Суттєвим недоліком цього комутатора є витрати на його реалізацію, що становлять (n2-n) пунктів з’єднань для n ПЕ. Практично така кількість пунктів може бути реалізована лише для невеликої кількості процесорів. Вже для 100 ПЕ потрібно 9900 перемикань, щоб забезпечити роботу вcix пунктів з’єднань.
Рис. 5.2. Розподілювач перехресних шин Дельта - сітки Щоб зменшити витрати, що виникають під час побудови розподілювачів перехресних шин, використовуються дельта-сітки (див. рис.5.3).
В найпростішому випадку (рис.5.3) дві лінії даних можуть перемикатись навхрест за допомогою єдиної лінії керування або на пряму передачу з входу на вихід. На рис.5.4 показано, як проходять сигнали всередині "чорного ящика" деякої дельта-сітки. Якщо керуючий сигнал дорівнює “нулю”, то обидві лінії даних (або пучки ліній) приєднуються прямо до вихідних ліній. У випадку, коли керуючий сигнал дорівнює “одиниці”, лінії даних перемикаються на виході навхрест.
Рис. 5.4. Перемикач дельта-мережі 3 таких простих базових елементів можна будувати більш об’ємні сітки. На рис.5.5 наведено триступеневу дельта-сітку, яка з’єднує 8 входів з 8 виходами. Кожний елемент сітки відповідає базисному елементу, що показаний на рис.5.3.
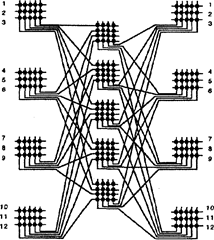
Рис. 5.5. Дельта-сітка розміром 8х8 Перевагою дельта-сіток над розподілювачами перехресних шин є менша кількість дельта-перемикачів, Комутуючі мережі Клоса Об’єднання кращих властивостей розподілювача перехресних шин та дельта-сіток зроблено в комутуючих мережах Клоса. Вимогою до цієї мережної структури є забезпечення довільної комбінації зв'язків між процесорами, тобто не допускається поява блокувань. 3 другого боку, витрати на реалізацію (кількість пунктів комутації) мають бути мінімальними. Це досягається побудовою мінімізованої за витратами багатоступеневої мережі. Причому елементи одного ступеню будуються на основі простіших малих розподілювачів перехресних шин. На рис.5.6 показано триступеневу мережу Клоса з N=12 входами, розподіленими на а=4 групи, кожна з яких має m=3 входів. У триступеневій мережі Клоса загальна кількість N ліній, що перемикаються повністю, реалізується в першій ступені а малими розподілювачами перехресних шин, кожний з яких має m входів i 2*(m-1) виходів (N=a*m). Друга ступінь побудована на 2*(m-1) розподілювачах перехресних шин, кожний з яких має а входів i а виходів, а третя - на розподілювачах з 2*(m-1) входами i m виходами. Параметром, який може вибиратися під час конфігурування мережі Клоса, є, таким чином, m. Загальна кількість пунктів комутації триступеневої мережі Клоса буде приблизно мінімальною, якщо m визначити за формулою:
Рис. 5.6. Трикаскадна мережа Клоса для N=12 (при а=4, m=3) При N³ 24, мережа Клоса ефективніша, ніж простий розподілювач перехресних шин. Загальна кількість пунктів комутації в триступеневій мережі Клоса визначається за формулою:
Вона містить (2*а) розподілювачі перехресних шин розміром “m:(2*m-1)” на ступенях 1, 3 i (2*m-1) розподілювача розміром " а:а " на ступені 2. 3 урахуванням того, що N=a*m, маємо:
Якщо кількість входів m оптимальна, то витрати на триступеневу мережу Клоса становлять приблизно На противагу цьому витрати на повний розподілювач перехресних шин відповідного розміру становлять приблизно N2. Приклад. Для триступеневої мережі Клоса з 1000 входами та виходами справедливо:
Беремо найближче m=20, що дає a=N/m= 50. Загальна кількість пунктів комутації буде:
Ця кількість значно менша, ніж у повному розподілювачі перехресних шин цього розміру:
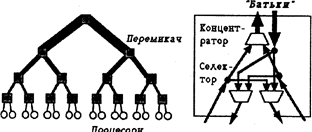
Таким чином, мережа Клоса заощаджує понад 82% пунктів комутації порівняно з розподілювачем перехресних шин. Розміри розподілювачів перехресних шин, що застосовуються як елементи мережі Клоса, вибирають відповідно до кількості комутованих процесорів i це виключає можливість блокувань зв'язків. Мережі типу Fat-Tree (батьківське дерево) Fat-Tree - решітчаста структура, що може масштабуватись як за кількістю процесорів, так i за кількістю можливих з’єднань, що відбуваються одночасно. Процесори - це листя повного двійкового дерева, в той час як внутрішні вузли - це ключові елементи (рис.5.7). Кількість процесорів - N=2m, а кількість ключів перемикання дорівнює N-1. Чим вище міститься ключовий елемент у дереві, тим більше ліній зв'язку перемикається в ньому (звичайно, немає потреби у подвоєній кількості ліній на кожному piвні дерева). Комутаційна структура Fat-Tree близька до оптимальної. Ця властивість робить її дуже цікавою для застосування в паралельних структурах.
Рис. 5.7. Мережа типу Fat-Tree та перемикач 4. Структури, що забезпечують зв'язок типу "пункт-пункт" Розгляньмо статичні структури зв’язку "пункт-пункт". Кільце Кільцева структура (рис.5.8) має дві лінії зв'язку на кожний ПЕ (перевага) i потребує в найгіршому випадку n/2 кроки для обміну даними мiж двома ПЕ, що розміщуються в кільці на найбільшій відстані один від одного (недолік).
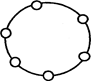 
Рис. 5.8. Кільце Повний граф Повний граф (рис.5.9) має оптимальну коннективність (кожний ПЕ зв’язаний безпосередньо з будь-яким іншим ПЕ) забезпечується n-1 лінією зв'язку на кожнийПЕ.
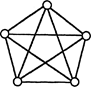
Рис. 5.9. Повний граф Решітки i тори Дуже часто застосовуються решітчасті структури зв'язку i їхні замкнуті варіанти - тори. На рис.5.10 показано різницю між чотири - i восьми - зв'язковими структурами.
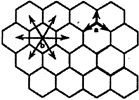
V=8; A= квадратна решітка (8 ліній зв’язку в ПЕ) Рис. 5.10. Квадратні решітки та тори Усі квадратні решітки мають максимальну відстань між ПЕ, що дорівнює квадратному кореню від кількості ПЕ. Збільшення кількості ліній вдвічі у восьмизв'язковій решітці робить відстань між ПЕ наполовину меншою. Такий самий ефект досягається переходом до замкнутого тора, в якому кількість ПЕ залишається без зміни. Гексагональна решітка. Гексагональна решітка може розглядатись як видозміна квадратної решітки. Залежно від того, де розміщені процесорні елементи (на перехресті чи в центрі, рис.5.11 а, б), вони потребують 3 або 6 ліній зв'язку.
а) ПЕ в кутку V=3 A=2*
б) ПЕ в центрі V=6 A=3/2* Рис. 5.11. Гексагональна решітка Кубічна решітка У кубічній решітці (рис.5.12) зроблено перехід від двовимірної до тривимірної решітки. Процесорні елементи розміщені в просторі куба потребують 6 ліній зв'язку з ПЕ - сусідами. Максимальна відстань між ПЕ тут зменшується, вона пропорційна
Рис. 5.12. Кубічна решітка Гіперкуб Гіперкуб нульової вимірності - це єдиний елемент (рис.5.13, ліворуч). Гіперкуб вимірності i+і виникає з двох гіперкубів вимірності і, в яких елементи, що взаємодіють, з’єднані між собою. Наприклад, на рис.5.13 показано, що з двох квадратів (гіперкубів вимірності 2) можна побудувати куб (гіперкуб вимірності 3), з’єднавши кожний елемент "переднього" з кожним елементом "заднього" квадрата. Гіперкуб є універсальною мережею зв'язку з невеликою логарифмічною відстанню i не дуже великою логарифмічною кількістю ліній зв'язку у кожного ПЕ.
Рис.5.13. Гіперкуб з розмірностями від нуля до чотирьох Двійкове дерево
Рис. 5.14. Двійкове дерево Пірамідальне дерево У цій структурі зв’язку (рис.5.15) кожна вершина має 4 послідовники в дереві що, може використовуватися для побудови алгоритмів розподілу образів у квадрантах.

Рис. 5.15. Пірамідальне дерево Ротація-зміна. (Shuffle-Exchange) До структур з логарифмічною вимірністю належить також мережа Shuffle-Exchange (ротація, або циклічний зсув та заміна). Вона складається з двох розділених видів зв'язку - одностороннього "Shuffle" та двостороннього "Exchange" (рис.5.16). N=2m V=2 (1 двонаправлена і 2 однонаправлені лінії) A=2log2n
Обидві структури зв'язку можуть бути дуже просто представлені за допомогою операції відображення номерів ПЕ бінарним способом запису (pi,-біт бінарного номера ПЕ, і=і,2,..m): Shuffle (pm, pm-1,..., p1,)=(pm-1,, p1, pm) - одна ротація вліво бінарного номера ПЕ ( m разів); Exchange (pm, p1)=(pm, p2 p1) - заміна молодшого біта бінарного номера ПЕ операцією заперечення. Shuffle - частина з’єднує кожний ПЕ з тим ПЕ, бінарний номер якого обчислюється циклічною операцією ротації вліво. Перший та останній елементи, що мають однакові двійкові розряди в номерах (на рис.5.16 це ПЕ Nо® 000, ПЕ N7 ®111) відображаються самі на себе, тоді як інші ПЕ з’єднані в цикли. Exchange - зв’язок у двійковій фopмi запису заперечує наймолодший біт ПЕ, тобто Exchange з’єднує двонаправлено кожний парний ПЕ з своїм правим сусідом. Приклад застосування операцій Shuffle та Exchange: 1) 001®010®100®001 2) 011®010®011 двосторонній зв'язок ПЕЗ «ПЕ2
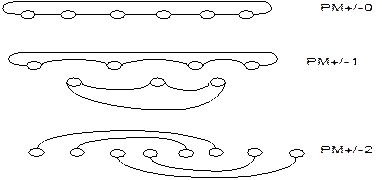
Плюс-мінус 2і- мережа (РМ2і) Мережа дещо складніша. При наявності п = 2m вузлів (вершин) мережі (процесорних елементів ПЕ) вона складається з 2*т‑1 окремих структур зв'язку, які позначаються як: РМ+0, РМ‑0, РМ+1, РМ.‑1, РМ+2, РМ.‑2,..., РМm‑1,. Для PMs справедливі такі визначення: РМ+1(j)=(j+2I)mod n; РМ.‑1(j)=(j-2I)mod n. Індекс кожної односторонньої структури показує, якою має бути відстань до сусідньої вершини (у двійковому порядку). Для РМ+0 відстань буде +2° =+1, для РМ‑0 відповідно -2° =-1 Відстань між вершинами для РМ+2 при цьому є +22 = +4, для РМ.‑2 буде - 4. Для вищого показника т-1 з урахуванням замкнутості структури має місце співвідношення: PM+(m-1)=PM - (m-1) Обидві структури ідентичні, тому є тільки 2*т-1, а не 2*т структур. На рис.5.17 показано мережу PM2I з n=8 ПЕ. РМ+0 i РМ‑0 зв'язують кожний ПЕ з своїм правим або лівим сусідом i створюють таким чином двостороннє кільце зв'язку., РМ+1, і РМ.‑1, включають дві розділені односторонні структури по чотири ПЕ. Кожний ПЕ має сусіда з номером через один, причому Modulo - операція утворює структуру зв'язку типу "кільце". Разом вони утворюють два окремих двосторонніх кільця. Остання структура РМ+2 ідентична з РМ.‑2 ,. Кожний ПЕ зв'язаний тут з іншим ПЕ на відстані 4 (Modulo 8). V=2*log2n-1 A= log2n-1
Рис. 5.17. Мережа типу PM2I
Порівняння мереж Порівняння мереж можливе тільки на основі параметрів V i А. Переваги, що має певна мережа, можна отримати тільки з урахуванням особливостей паралельної задачі. Якщо алгоритм розв'язування задач потребує певної мережі, то, як правило, фізична реалізація якраз цієї, можливо “гіршої” за параметрами V i А мережі, дасть кращі результати, ніж пристосування для цієї задачі іншої мережі, що має "хороші" параметри. Для вирішення кожної проблеми неможливо будувати спеціалізовану систему. Кожна паралельна система має у своєму розпорядженні декілька комутаційних структур, які можуть бути багатосторонніми i здатними до динамічної конфігурації. Усі алгоритми, які підлягають імплементації в цій паралельній системі, мають задовольнятися наявною мережею (або її частиною). Цінність мережі залежить, таким чином, від того, наскільки якісно вона може використовуватись в середньому для вирішення проблем, що постають найчастіше. Наприклад, паралельна ЕОМ MasPar МР-1 функціонує із застосуванням двох різних мереж: решітчастої структури та триступеневої мережі Клоса, що забезпечує хорошу загальну коннективність. Алгоритми, які потребують решітчастої структури, можуть використовувати безпосередньо цю швидку локальну структуру, тоді як алгоритми, яким потрібні інші мережні структури, можуть бути реалізовані з використанням маршрутизації на глобальній мережі Клоса з деякими втратами ефективності. 3ігель моделював одні мережі з застосуванням інших мереж. При цьому виявляється передусім перевага Shuffle-Exchange та гіперкуба як "універсальних мереж", тобто як засобів ефективної емуляції декількох piзноманітних мережних структур. Решітка тільки тоді виправдана, коли решітчаста структура потрібна для реалізації алгоритмів; для моделювання інших мереж вона непридатна. Насамперед емуляція мережі може бути виконана автоматично компілятором лише тоді, коли крім мережної структури цільової системи відома також структура, яка потрібна для реалізації прикладної програми. Найчастіше реляції про міжпроцесорні зв'язки, що мають забезпечити обмін даними, задані у вигляді складних арифметичних виразів, мало відрізняються від "стандарту" або взагалі обчислюються i стають відомими лише перед запуском програм. В табл.5.1 показано кількість потрібних циклів моделювання залежно від кількості її процесорних елементів. Таблиця 5.1. Порівняння комутаційних мереж
Методи комутацій Важливим в організації роботи комутаційної мережі є метод перемикання, який визначає як повідомлення передаються від вузла-передавача до вузла-приймача. Передача здійснюється повідомленнями і пакетами. Виділяють три основних методи комутації в комутаційних мережах паралельних систем: - комутація з проміжковим зберіганням (“зберігання- і передача” – Store-and-forward); - комутація каналів; - комутація віртуальних каналів. В першому випадку повідомлення повністю приймається на проміжному вузлі і тільки після цього передається далі. Пересилка виконується як тільки звільнився черговий канал передачі, тоді повідомлення передається на наступний вузол. Буферизація вимагає додаткової пам’яті і затрат часу. Метод використовується тоді, коли час відклику не суттєвий. При комутації каналів між джерелом і одержувачем повідомлення встановлюється неперервний зв'язок, після чого виконується передача даних. Комутуючий канал встановлюється тільки на час з’єднання. Приклад – телефонний зв'язок. Зменшити затримки при передачі даних дозволяє метод віртуальних каналів. В цьому випадку пакети накопичуються в проміжних вузлах тільки тоді, коли недоступний черговий канал зв’язку. В іншому випадку пересилка виконується негайно і без буферизації.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 .
.

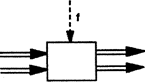 Рис. 5.3. Дельта-мережі комутації
Рис. 5.3. Дельта-мережі комутації

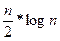 . Головним недоліком є те, що не вci можливі комбінації зв'язків між процесорами можуть бути реалізовані. Тут можуть виникати блокування, для запобігання яким треба використовувати спеціальні концепції програмування. Блокування суттєво затримує виконання паралельної програми, що зумовлено необхідністю пepeкoнфiгypaцiї комутуючої сітки та побудови нової схеми сполучень між процесорами. Ця ситуація аналогічна тій, що має місце в телефонних мережах.
. Головним недоліком є те, що не вci можливі комбінації зв'язків між процесорами можуть бути реалізовані. Тут можуть виникати блокування, для запобігання яким треба використовувати спеціальні концепції програмування. Блокування суттєво затримує виконання паралельної програми, що зумовлено необхідністю пepeкoнфiгypaцiї комутуючої сітки та побудови нової схеми сполучень між процесорами. Ця ситуація аналогічна тій, що має місце в телефонних мережах.
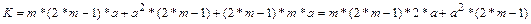
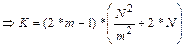
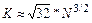 .
.
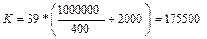
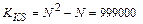
 V=4; A=2*
V=4; A=2* 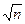 -2 = 2*
-2 = 2* 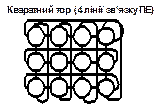 V=4; A=
V=4; A= 
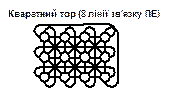 V=8 A=
V=8 A= 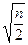

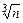 .
. V=6; A=3*
V=6; A=3* 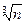 -3
-3 n=2m; V=log2n A=log2n
n=2m; V=log2n A=log2n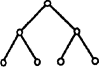


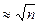 /2
/2
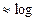 2n
2n
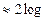 2n
2n
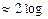 2n
2n
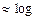 2n+1
2n+1



