
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраїчне доповнення елемента.Содержание книги
Поиск на нашем сайте
Нехай дана квадратна матриця n-го порядку A = Означення. Мінором (n-1)-го порядку М квадратної матриці А n-го порядку називається детермінант матриці (n-1)-го порядку, який утворений з матриці А викресленням i-го рядка та j-го стовпчика. Матриця А n-го порядку має n2 мінорів (n-1)-го порядку. Означення. Алгебраїчним доповненням елемента аij квадратної матриці А n-го порядку називається мінор Мij матриці А, помножений на (-1)i+j, тобто Аij=(-1)i+jМij Приклад 1. Обчислити всі мінори і алгебраїчні доповнення 2-го порядку визначника
M11 = M12 = M13 = A11 = -3, A12 = 3, A13 = -1, A21 = 1, A22 = -1, A23 = 1, A31 = 7, A32 = -5, A33 = 1. Лема. Детермінант D, в якого всі елементи i-го рядка (або j-го стовпця), крім елемента аij, дорівнюють нулю, дорівнює добутку елемента аij на його алгебраїчне доповнення, тобто D=аijАij. Теорема. Визначник D=ïаijï n-го порядку дорівнює сумі всіх попарних добутків елементів будь-якого рядка або стовпця на їх алгебраїчні доповнення, тобто D=аi1Аi1+…+аinАin, D=а1jА1j+…+аjnАj1 Перша з них – це розклад детермінанта за елементами i-го рядка, друга – розклад детермінанта за елементами j-го стовпця. Наслідок. Детермінант квадратної матриці n-го порядку дорівнює нулю, якщо всі мінори (n-1)–го порядку дорівнюють нулю. Теорема. Сума всіх попарних добутків елементів будь-якого рядка (стовпця) визначника на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) цього визначника дорівнює нулю. Наслідок. a1jА1m+…+аnjАnm=0 (j¹m) ai1Ak1+…+ainAkn=0 (i¹k). Приклад 2. Обчислити детермінант 1 спосіб. Розкладемо детермінант за елементами першого стовпчика D= + 5(-1)4 =3(-28+120-24-140-36-16)-(56+240-42-245-72+32)+5(24+120+14- 2 спосіб. За допомогою елемента a21 = 1 обнулимо всі інші елементи першого стовпчика і для обчислення використаємо лему D= = -(1120+468+1040-520--672-1560)=124.
Детермінант n-го порядку. Означення. Детермінантом n-го порядку квадратної матриці називається алгебраїчна сума n! членів (доданків), кожен з яких є добутком n елементів, взятих з різних рядків і з різних стовпчиків, причому цей добуток береться із знаком плюс, якщо перестановка, утворена з других індексів (при умові, що перші йдуть по порядку), парна, і з протилежним знаком, якщо ця перестановка непарна. Використовуючи вище сказане, пояснимо знаки доданка а13а21а32 та а12а21а33. Розташуємо перші індекси по порядку, а з других утворимо перестановку 3,1,2 та 2,1,3 відповідно. Перша перестановка є парною, тому знак доданка а13а21а32 плюс, а друга – непарна, тому знак доданка а12а21а33 – мінус. Властивості детермінанта n-го порядку: 1) Якщо в детермінанті є нульовий рядок, то детермінант дорівнює нулю. 2) Перестановка рядків (стовпчиків) змінює знак детермінанта. 3) Якщо в детермінанті є два однакові рядки, то детермінант дорівнює нулю. 4) Спільний множник k з одного рядка (стовпчика) можна винести за знак детермінанта. 5) Якщо в детермінанті якийсь рядок є сумою двох рядків, то 6) Якщо в детермінанті є два пропорційні рядки (стовпчики), то детермінант дорівнює нулю. 7) Якщо в детермінанті k-ий рядок домножити на число р≠0 і додати його до m-го рядка, то детермінант не зміниться.
8) Детермінант не змінюється при транспонуванні. Транспонування – перехід від даного детермінанта до нового, одержаного з даного за таким правилом: всі рядки детермінанта записуються відповідними стовпчиками в новому детермінанті. 9) Сума добутків елементів рядка на чужі алгебраїчні доповнення дорівнює нулю. Сума добутків елементів рядка на свої алгебраїчні доповнення дорівнює детермінанту. Приклад. 1) Розв’язати систему рівнянь методом Крамера:
А = D = D1 = D2 = D3 = Розв’язок х=(15,59/5,92/5). 2) Розв’язати систему рівнянь методом Крамера:
D = D1 = D2 = D3 = Система несумісна. 3) Розв’язати систему рівнянь методом Крамера:
D = D1 = D2 = D3 = Систему методом Крамера розв’язати не можна. Складемо розширену матрицю системи і зведемо її до діагонального виду.
Загальний розв’язок х=(
§4. Деякі застосування визначників. Теорема 1. Для того, щоб детермінант квадратної матриці дорівнював нулю, необхідно і достатньо, щоб ранг цієї матриці був менший її порядку. Наслідок 1. Детермінант дорівнює нулю тоді і тільки тоді, коли його рядки (стовпці) утворюють лінійно залежну систему векторів. Наслідок 2. Квадратна матриця є особливою тоді і тільки тоді, коли її детермінант дорівнює нулю. Наслідок 3. Добуток двох неособливих матриць – неособлива матриця. Добуток двох матриць, хоча б одна з яких особлива, - особлива матриця. Нехай дана прямокутна матриця А = Теорема. (про ранг матриці) Для того, щоб ранг матриці дорівнював r, необхідно і достатньо, щоб серед мінорів матриці знайшовся хоча б один мінор r-го порядку, відмінний від нуля, а всі його мінори (r+1)-го порядку дорівнювали нулю. Означення. Рангом матриці називається найвищий порядок мінорів цієї матриці, відмінних від нуля. Приклад. Обчислити ранг матриці методом окантування мінорів: А = М1 ¹ 0 M2 = M3 = M3 = M3 = M3 = M4 = Перевірка: r(A) = 3
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 848; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.110.231 (0.006 с.) |



 = -3 M21 =
= -3 M21 = 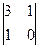 = -1 M31 =
= -1 M31 =  = 7
= 7 = -3 M22 =
= -3 M22 =  =-1 M32 =
=-1 M32 =  = 5
= 5 = -1 M23 =
= -1 M23 = 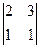 = -1 M33 =
= -1 M33 =  = 1
= 1 = 3(-1)2
= 3(-1)2  + 1(-1)3
+ 1(-1)3  +
+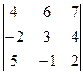 + 4(-1)5
+ 4(-1)5 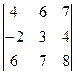 =
= =
=
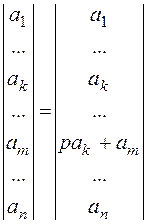
 =(-1)1+iMi1ak1+…+(-1)i+nMinakn = =ak1Ai1+ak2Ai2+aknAin = 0
=(-1)1+iMi1ak1+…+(-1)i+nMinakn = =ak1Ai1+ak2Ai2+aknAin = 0
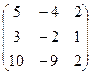 В =
В = 
 = -20-40-54+40+24+45 = -5
= -20-40-54+40+24+45 = -5 = 36-28-54+28-81+24 = -75 х1 = -75/(-5) = 15
= 36-28-54+28-81+24 = -75 х1 = -75/(-5) = 15 = 30-90+42-60+54-35 = -59 x2 = -59/(-5) = 59/5
= 30-90+42-60+54-35 = -59 x2 = -59/(-5) = 59/5 = -70+243-120-180+84+135 = 92 x3 = 92/(-5)= = -92/5
= -70+243-120-180+84+135 = 92 x3 = 92/(-5)= = -92/5
 = -4-8-5+4+8+5 = 0
= -4-8-5+4+8+5 = 0 = -4-12-10+6+16+5 = 1
= -4-12-10+6+16+5 = 1 = -4-2-3+4+2+3 = 0
= -4-2-3+4+2+3 = 0 = 6+16+5-4-12-10 = 1
= 6+16+5-4-12-10 = 1
 = -48-6-45+12+15+72 = 0
= -48-6-45+12+15+72 = 0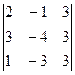 = -24-6-27+12+9+36 = 0
= -24-6-27+12+9+36 = 0 = 36+12+15-9-30-24 = 0
= 36+12+15-9-30-24 = 0 = -16-3-30+8+5+36 = 0
= -16-3-30+8+5+36 = 0

 ,
,  , x3), x3 є R.
, x3), x3 є R.

 = -16+5 = -11
= -16+5 = -11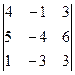 = -48-6-45+12+72+15 = 0
= -48-6-45+12+72+15 = 0 = 0
= 0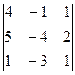 = -16-2-15+4+5+24 = 0
= -16-2-15+4+5+24 = 0 = 2(-1)6
= 2(-1)6  = 2
= 2 




