
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зміна рядків. Перестановочна матрицяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Розв’язати систему лінійних рівнянь Ах = b, де
В такому випадку розкласти матрицю А=LU неможливо. Існують спеціальні матриці, при множенні на які можна переставити рядки. Матриця Матриця
Матриця РА вже трикутна. Розв’яжемо систему лінійних рівнянь РАх = Рb.
Даний розв’язок і буде розв’язком системи лінійних рівнянь Ах = b. В загальному випадку перестановочна матриця Р переставляє рядки матриці А, уникаючи нулів на головній діагоналі. В цьому випадку РА може бути розкладена на LU, тобто РА = LU. Приклад. Знайти розклад РА=LDU для матриці А=
§3. Прямокутні матриці з ортонормованими стовпцями. Нехай маємо три незалежних вектора а, b, с. Ортогоналізуємо дану систему векторів.
Вектор
Вектор
В результаті ми одержали ортонормовану систему векторів, які утворюють ортогональну матрицю Q. Процес Грамма-Шмідта починається з незалежних векторів а1, а2,..., аn і закінчується ортонормованими векторами q1, q2,…, qn. На j-ому кроці віднімаємо від аj його координати в напрямках, які вже встановлені:
§4. Розклад А=QR Встановимо зв’язок між матрицями A і Q. Вектори а і q1 лежать на одній прямій. Кожен вектор площини є лінійною комбінацією векторів q1 і q2 : Аналогічно с є лінійною комбінацією векторів q1, q2, q3:
Виразивши це в матричній формі отримаємо новий розклад А=QR.
Розклад A=QR подібний до A=LU, але зараз перший множник Q має ортонормовані стовпці, а другий множник R – верхня трикутна матриця.
Приклад 1. Знайти розклад матриці А=QR
Приклад 2. Знайти розклад матриці А=QR
Можливо розклад QR є не такий гарний, як LU (тому, що є квадратні корені), але обидва розклади є важливими в курсі лінійної алгебри. Розклад LU ввів Герц, а розклад QR ввів Авіс. Зауваження. Кожну матрицю А розмірності можна розкласти на множники A=QR. Колонки Q є ортонормованими, а матриця R верхня трикутна. Якщо m=n, то всі матриці квадратні і Q стає ортогональною матрицею. Приклад 3. Розв’язати систему лінійних рівнянь, використовуючи розклад А=QR.
Отримаємо систему лінійних рівнянь
Інші цікаві розклади матриць Використовуючи розклади матриці А можна розв’язати систему лінійних рівнянь Ах = b, якщо: 1. A=LU, тоді Lc=b, Ux=c, x=U-1L-1b; 2. A=QR, тоді Qc=b, Rx=c, x=R-1QTb. Розглянемо розклади матриць: 1. Розклад Чолескі для симетричної матриці А:
де 2. Скорочений розклад:
де матриці мають такі розмірності 1. Якщо матриця А симетрична, то LT =U і в такому випадку A=LDLT=LDU.
Приклад 1.
Приклад 2.
Матриця 2. Скорочений розклад Подібно симетричному розкладу LDLT він є кращий, ніж A=LU, але дещо відрізняється. Якщо А має ранг r, ми маємо тільки r стовпців в матриці L і r В кожному випадку r стовпців Приклад. Розкласти матрицю
Задачі 1. Розкласти на множники L і U матриці:
2. Розкласти на множники L і U матрицю А і розв’язати систему лінійних рівнянь
3. Знайти розклад РА=LDU
4. Розкласти матрицю А на множники Q і R
5. Розкласти матрицю А на множники Q і R
6. Розв’язати систему лінійних рівнянь використовуючи розклад А=QR
7. Розкласти матрицю 8. Для матриці 9. Розкласти матрицю А на множники
10. Зробити розклад Чолескі для матриці А:
Бібліотека термінів
А Абелева група – група, в якій операція комутативна, тобто "a "b (a*b=b*a) Алгебра – множина із введеними на ній алгебраїчними операціями. Алгебраїчним доповненням А елемента аij квадратної матриці А n-го порядку називається мінор Мij матриці А, помножений на (-1)i+j, тобто Аij=(-1)i+jМij
Б Базис – лінійно незалежна підсистема аi1,аi2,…,аin системи векторів а1,а2,…,аm простору Vn, якщо кожний вектор даної системи є лінійною комбінацією векторів підсистеми. Базис векторного простору – лінійно незалежна система твірних. В Векторний (лінійний) простірнад полем Р – множина елементів довільної природи, в якій введено операції додавання і множення на елементи поля (скаляри) і виконуються аксіоми: 1) <Vn,+> - абелева група; 2) Операція множення на скаляр асоціативна " k,l є P, " a є Vn ((kl)a=k(la)); 3) " a є Vn (1*a=a), 1 4) Операція множення на скаляр дистрибутивна відносно додавання елементів множини Vn " k є P " a,b є Vn (k(a+b)=ka+kb); 5) Операція множення на скаляр дистрибутивна відносно додавання скалярів " k,l є P " a є Vn ((k+l)a=ka+kb). Визначена система лінійних рівнянь – сумісна система лінійних рівнянь, яка має єдиний розв’язок. Власний вектор оператора А – вектор а¹0, який задовольняє умові аА=lа, де l є Р. Власне значення оператора А – число l, яке відповідає власному вектору а такому, що аА=lа.
Г Головна діагональ квадратної матриці n-го порядку – діагональ, яка йде від лівого верхнього кута до нижнього правого, тобто яка складається з елементів а11,а22,…,аnn. Група – множина G із введеною на ній алгебраїчною операцією *, якщо виконуються такі властивості: 1) асоціативність операції " a,b,c є G ((a*b)*c=a*(b*c)); 2) нейтральний елемент " a є G $ e (a*e=e*a=a); 3) симетричний елемент " a є G $ a¢ (a*a¢=a¢*a=e). Д Детермінант n-го порядку квадратної матриці – алгебраїчна сума n! членів (доданків), кожен з яких є добутком n елементів, взятих з різних рядків і з різних стовпчиків, причому цей добуток береться із знаком плюс, якщо перестановка, утворена з других індексів (при умові, що перші йдуть по порядку), парна, і з протилежним знаком, якщо ця перестановка непарна Дефект лінійного оператора dim(KerA) – розмірність ядра цього оператора. Діагональна матриця – квадратна матриця D = (dij) n-го порядку, якщо всі її елементи, які не належать головній діагоналі, дорівнюють нулю "i, j (i¹ j => dij=0). Дійсний векторний (лінійний) простір – простір Vn, якщо поле Р - це поле дійсних чисел. Добутоквектора a=(a1,a2,…,an) на число k є P – вектор ka=(ka1,ka2,…,kan). Добуток матриці А на елемент k є P – матриця kA = (kаij)m*n. Добуток матриці А на матрицю В – матриця АВ = (сpq)m*l, де А=(аij)m*n, В=(bsk)n*l, сpq=ap1b1q+ap2b2q Добуток лінійних операторів А і В – оператор D, який визначається формулою " х є Vn (xD=(xA)B) і позначається D=AB. Добуток лінійного оператора А на число k – оператор В, який визначається формулою " х є Vn k є Р (хВ=kxA) і позначається В=kA. Довжина (норма) вектора а - невід’ємне значення квадратного кореня з числа (а,а), позначається êêа êê.
Е Евклідовий простір – дійсний векторний простір, в якому визначений скалярний добуток. Елементарні перетворення матриці А: 1) перестановка рядків (стовпчиків); 2) множення рядка (стовпчика) на довільне, відмінне від нуля число; 3) додавання рядків (стовпчиків); 4) множення рядка (стовпчика) і додавання його до іншого рядка (стовпчика). Елементарні перетворення системи лінійних рівнянь: 1) перестановка місцями (транспозиція) двох рівнянь системи; 2) множення будь-якого рівняння системи на число, відмінне від нуля; 3) додавання до одного рівняння системи іншого її рівняння, помножене на деяке число; 4) викреслення невизначеного рівняння. І Ідемпотентна матриця – матриця, якщо А2=А. Інваріантний підпростір U лінійного простору Vn відносно оператора А – такий підпростір, що UAÍU, тобто якщо образ хА довільного вектора х з U міститься в U. Інверсія – упорядкована пара (i,j), якщо i > j. i-ий діагональний елемент – елемент головної діагоналі матриці.
К Квадратна матриця n-го порядку – матриця, в якої кількість рядків дорівнює кількості стовпців. Кільце – множина <K,+,* >, якщо: 1) <K,+> - абелева група; 2) * - асоціативна; 3) дистрибутивні закони "a,"b,"c є K ((a+b)c=ac+bc) ((a+b)=ca+cb). Комутативне кільце – кільце, в якому операція множення комутативна. Кососиметрична матриця - квадратна матриця, для якої A¢=-А. Кут між векторами a i b (ненульовими) евклідового простору Е – таке число j (0<=j<=p), що Л Лінійно залежна система векторів – система векторів а1,а2,…,аm простору Vn, якщо існують такі числа k1,k2,…,km не всі рівні нулю, що k1a1 +k2a2+…+kmam=0(*) Лінійна комбінація векторів а1,а2,…,аm - вектор b є Vn, якщо існують такі числа k1,k2,…,km, що b=k1a1+k2a2+…+kmam. Числа k1,k2,…,kn називаються коефіцієнтами цієї лінійної комбінації. Лінійний многовид простору V – множина всіх векторів х=х0+y, де х0 – деякий вектор простору V,а y – будь-який вектор підпростору V¢ простору V. Лінійно незалежна система векторів – система векторів для якої рівність (*)виконується лише при k1 = k2 = … = km = 0. Лінійна оболонка системи векторів (простір, натягнутий на дану систему векторів) L(a1,a2,…,am) – множина всіх лінійних комбінацій векторів даної системи векторів. L(a1,a2,…,am)={k1a1+k2a2+…+kmam êki є Р, i=1,…,m}. Лінійний оператор А векторного простору V – оператор для якого виконуються такі умови: 1) " х1,х2 є L ((х1+х2) А =х1 А +х2 А); 2) " х є L " k є P ((kх) А =k(х А)). Лінійне рівняння з n невідомими – рівняння виду а1х1+а2х2+…+аnхn=b, де х1,х2,…,хn – невідомі, а1,а2,…,аn – числа з деякого числового поля Р. Числа а1,а2,…,аn називають коефіцієнтами рівняння, а число b – вільним членом цього рівняння. М Матриця – прямокутна таблиця, яка складається з елементів даного поля. Загальний вигляд матриці: A = А = (a1,a2,…,an) В = Мінором (n-1)-го порядку квадратної матриці А n-го порядку – детермінант матриці (n-1)-го порядку, який утворений з матриці А викресленням i-го рядка та j-го стовпчика. Множенням матриць – операція, яка матрицям А і В ставить у відповідність матрицю АВ = (сpq), де сpq = ap1b1q+ap2b2q+…+apnbnq, тобто сpq є сумою добутків відповідних елементів р-го рядка і q-го стовпчика. Н Невизначена система лінійних рівнянь -система лінійних рівнянь, якщо вона має безліч розв’язків Невизначене рівняння – рівняння виду 0*х1+0*х2+…+0*хn = 0. Несумісна система рівнянь – система рівнянь, яка не має жодного розв’язку. Неособлива (невироджена) матриця – квадратна матриця, яка не є особливою. Непарна перестановка – перестановка, в якій загальна кількість інверсій непарна. Нормований вектор – вектор, довжина (норма) якого дорівнює 1. n-мірним арифметичним простором над полем Р – множина Vn всіх n-мірних числових векторів з координатами із поля Р із введеними на ній операціями додавання векторів і множення вектора на число з поля Р. n-мірний числовий вектор - будь-яка впорядкована система n чисел a1,a2,…,an з поля P (деяке числове поле); числа a1,a2,…,an називаються його координатами (компонентами): a1–першою координатою, a2–другою координатою,…, an–n-ою координатою. О Обернена матриця – матриця А-1, яка має таку властивість АА-1 = А-1А = Е, де Е – одинична матриця відповідного порядку. Область значень ІmA лінійного оператора А – сукупність образів всіх векторів простору Vn. Оборотна матриця - матриця, для якої існує обернена матриця. Однорідне рівняння –лінійне рівняння а1х1+а2х2+…+аnхn = b, якщо його вільний член b дорівнює нулю. Ортогональна матриця – квадратна матриця, якщо АА¢ = A¢A = E. Ортогональна система векторів – система векторів а1,а2,…,аn, якщо будь-які її два вектори ортогональні, тобто (аi,аj) = 0 для i ¹ j. Ортогональне доповнення підпростору U – підпростір U^ всіх векторів простору Е, ортогональних підпростору U. Ортогональні вектори – вектори a i b простору Е, якщо (a,b) = 0. Ортогональний підпростору U вектор a – вектор простору Еn, якщо він ортогональний довільному вектору цього підпростору (записують а ^U). Ортонормований базис - базис е1,е2,…,еn евклідового простору Еn, якщо він ортогональний і всі його вектори нормовані, тобто (еi,еj) = Основна матриця СЛР – матриця, яка складена з коефіцієнтів СЛР. Особлива (вироджена) матриця - квадратна матриця, якщо ранг матриці менший її порядку.
П Парна перестановка – перестановка, в якій загальна кількість інверсій парна. Парність підстановки – сума числа інверсій у верхній і нижній перестановці. Переріз підпросторів А,В,С,… - множина F=AÇBÇCÇ… векторів, які належать одночасно кожному з просторів А,В,С,…, де А,В,С,… - скінченна або нескінченна множинадеяких підпросторів простору V. Перестановкою з n елементів – послідовність, утворена внаслідок впорядкування n-елементної множини. Підпростір – непорожня підмножина V¢ векторного простору Vn, якщо вонa є лінійним простором відносно операцій, введених у Vn. Підсистема - множина, яка складається з будь-яких k (k£m) векторів системи а1,а2,…,аm. Підстановкою з n елементів – бієктивне відображення n-елементної множини на себе. Поле – комутативне кільце з одиницею, в якому " a ≠ 0 $ a-1 (a*a-1 = 1). Пропорційний вектор b з простору Vn вектору a з цього ж простору, якщо існує таке число k таке, що b=ka. Пряма сума підпросторів – сума U=U1+U2+…+Um лінійних підпросторів U1,U2,…,Um простору V, якщо для довільного вектора u є U існує тільки одне представлення виду u = u1+u2+…+um, де ui є Ui, i = 1,…,m. Прямокутна матриця – матриця розміру m*n, якщо m ¹ n.
Р Рангматриці – найвищий порядок мінорів цієї матриці, відмінних від нуля. Ранг RangA лінійного оператора А – розмірність області значень ImА. Ранг системи векторів – кількість векторів, які входять в будь-який базис даної системи векторів. Рівні вектори – числові вектори a = (a1,a2,…,an), b = (b1,b2,…,bn), якщо рівні їх відповідні координати, тобто а = b ó a1 = b1 Ù a2 = b2 Ù … Ù an = bn. Рівні матриці – матриці, в яких рівні відповідні елементи. Рівносильні системи лінійних рівнянь – системи лінійних рівнянь, множини розв’язків яких співпадають Розв’язок рівняння – n-мірним числовий вектор а = (а1,а2,…,аn) такий, що рівняння перетворюється в істинну рівність після заміни в ньому невідомих хi відповідними координатами аi. Розв’язок системи лінійних рівнянь – будь-який n-мірний числовий вектор а = (а1,а2,…,аn), який є розв’язком кожного з рівнянь цієї системи. Розмірністю многовиду Р – розмірність того підпростору V¢, зсувом якого було одержано цей многовид. Розширена матриця – матриця, яка складена з коефіцієнтів і вільних членів системи. Рядковий ранг матриці – ранг системи векторів-рядків матриці. С Симетрична матриця – довільна квадратна матриця А, якщо A¢=A. Система лінійних однорідних рівнянь (СЛОР) – систем лінійних рівнянь, в якій всі вільні члени дорівнюють нулю. Система лінійних рівнянь (СЛР) – система виду
де х1,х2,…,хn - невідомі, а11,а12,…,аmn і b1,b2,…,bm - деякі числа з поля Р. Числа а11,а12,…,аmn називаються коефіцієнтами системи, а числа b1,b2,…,bm – вільними членами системи. Система твірних – система векторів а1,а2,…,аn множини векторів лінійного простору, якщо будь-який вектор з цієї множини можна лінійно виразити через скінченне число векторів а1,а2,…,аn: a1,а2,…,аn – система твірних º "аi (аi=k1a1+k2a2+…+knan). Скалярна матриця – діагональна матриця, якщо елементи її головної діагоналі рівні між собою. Скалярне множення – операція, що кожній парі векторів a,b є Vn ставить у відповідність єдине дійсне число, яке називається скалярним добутком векторів a,b і познaчається символом (a,b), причому виконуються аксіоми скалярного добутку: 1. " a,b є Vn [(a,b) = (b,a)]; 2. " a,b є Vn [(a+b,c) = (a,c)+(b,c)]; 3. " a,b є Vn " k є R [(ka,b) = k(a,b)]; 4. " a є Vn, a ¹ 0 [(a,a) ³ 0]. Спектром лінійного опереатора А – весь набір характеристичних коренів оператора А. Стовпчиковий ранг матриці –ранг системи векторів-стовпчиків матриці А. Сума векторів – вектор c=(a1+b1,a2+b2,…,an+bn), де a =(a1,a2,…,an), b=(b1,b2,…,bn). Сума матриць А+В – матриця (аij+bij)m*n, де А = (аij)m*n, В = (bij)m*n над полем Р Сума операторів А+В – оператор S, який кожному вектору х є Vn ставить у відповідність вектор хА+хВ і позначається S=A+B Сума підпросторів U1,U2,…,Um - множина U = U1+U2+…+Um всіх векторів, кожний з яких представляється у вигляді суми u1+u2+…+um, ui є Ui. Сумісна система рівнянь – система рівнянь, яка має хоча б один розв’язок. Суперечливе рівняння – рівняння виду 0*х1+0*х2+…+0*хn = b, b ¹ 0.
Т Транспозиція – зміна місцями двох елементів перестановки. Транспонування детермінанта – перехід від даного детермінанта до нового, одержаного з даного за таким правилом - всі рядки детермінанта записуються відповідними стовпчиками в новому детермінанті. Транспонування матриці – перехід від даної матриці до нової, одержаної з даної за таким правилом - всі рядки матриці записуються відповідними стовпчиками в новій матриці. Ф Фундаментальною системою розв’язків - будь-яка лінійно незалежна система векторів однорідної системи лінійних рівнянь, через яку лінійно виражається довільний розв’язок цієї системи. Х Нехай А=(аij) – деяка матриця n-го порядку над полем Р. Е – одинична матриця порядку n, l - деяке невідоме, тоді матриця А-lЕ називається характеристичною матрицею матриці А. А = Характеристичним рівнянням матриці А – рівняння êА-lЕ ê= 0. Характеристичні корені матриці А – корені êА-lЕ ê= 0. Характеристичне рівняння оператора А - характеристичне рівняння êА-lЕ ê=0 матриці А. Характеристичні корені оператора А – корені êА-lЕ ê=0. Я Ядро KerA лінійного оператора А простору V – сукупність всіх векторів цього простору, які відображаються оператором А в нульовий вектор q KerA = { x êx є V, xA = q} Ì V
1. Завало С.Т. Алгебра і теорія чисел. К., 1983 2. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел. К.-1977. ч.1. 3. Збірник задач з лінійної алгебри та аналітичної геометрії.//Діскант В.І., 4. Крутицкая Н.И., Шишкин А.А. Линейная алгебра в вопросах и задачах.М.-1975 5. Курош А.Г. Курс высшей алгебры. М.- 1971 6. Мальцев А.И. Основы линейной алгебры. М.-1975 7. Нечаев В.А. Задачник-практикум по алгебре. Гуппы, кольца, поля. М.- 1983 8. Проскуряков И.В. Сборник задач по линейной алгебре. М.-1965 9. Фадєєв Д.К. Сомінський І.С. Збірник задач з вищої алгебри М.-1971 10. Linear Algebra and its applications. Gilbert Strang. Massachusetts Institute of Technology.
Зміст Розділ 1. Векторні простори та системи лінійних рівнянь. 3 §1. Вектори. Дії над векторами. 3 §2. Поняття системи лінійних рівнянь і її розвязків. 4 §3. Елементарні перетворення. 7 §4. Векторні простори.Арифметичний n-мірний векторний простір. 10 §5. Лінійна залежність векторів. 13 §6. Базис і ранг скінченної системи векторів векторного простору. 15 §7. Однорідні системи лінійних рівнянь. Фундаментальна система розв’язків однорідної системи. 17 §8. Зв’язок між розв’язками неоднорідних і однорідних систем. 20 §9. Лінійний многовид. 22 Розділ 2. Матриці та дії над матрицями. 23 §1. Матриці. 23 §2. Дії з матрицями. 25 §3. Частинні випадки множення матриць. 28 §4. Обернена матриця. 31 §5. Ранг матриці. 32 § 6. Матрична форма системи лінійних рівнянь. 34 Розділ 3. Визначники. 39 §1. Детермінант (визначник) квадратної матриці. Детермінант другого §2. Алгебраїчне доповнення елемента. 41 §3. Детермінант n-го порядку. 43 §4. Деякі застосування визначників. Обчислення рангу матриці. 48 §5. Обчислення оберненої матриці. 49 Розділ 4. Підпростори векторних просторів. 51 §1. Лінійна оболонка системи векторів. 51 §2. Переріз і сума підпросторів. 51 §3. Пряма сума підпросторів. 54 Розділ 5. Евклідові простори. 55 §1. Скалярний добуток та евклідові простори. 55 §2. Довжина вектора. Кут між векторами. 56 §3. Ортогональний базис. 57 §4. Ортонормований базис. 58 §5. Ортогональне доповнення підпростору. 58 Розділ 6. Лінійні оператори векторного простору. 65 §1. Лінійні оператори і їх матриці. 65 §2. Способи задання лінійного оператора. 66 §3. Зв’язок між матрицями лінійного оператора в різних базисах. 68 §4. Операції над лінійними операторами. 69 §5. Область значень і ядро лінійного оператора. Ранг і дефект лінійного оператора. 70 §6. Інваріантні підпростори. Власні вектори і власні значення лінійного оператора. 71 §7. Характеристичне рівняння лінійного оператора. 72 §8. Лінійний оператор з простим спектром. 73 Розділ 7. Цікаві розклади матриць та їх застосування для розв’язування систем лінійних рівнянь. 84 §1. Трикутний розклад і зміна рядків. 84 §2. Зміна рядків. Перестановочна матриця. 87 §3. Прямокутні матриці з ортонормованими стовпцями. §4. Розклад А=QR.. 89 §5. Інші цікаві розклади матриць. 93 §6. Задачі 97 Список використаних джерел. 111
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.015 с.) |


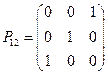 переставляє 1 і 2 рядки.
переставляє 1 і 2 рядки. переставляє 2 і 3 рядки.
переставляє 2 і 3 рядки.







 - одиничний вектор.
- одиничний вектор.
 ортогональний вектору
ортогональний вектору 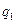 .
. - одиничний вектор.
- одиничний вектор.
 ортогональний до
ортогональний до  .
.
 і
і  - одиничний вектор.
- одиничний вектор. .
.



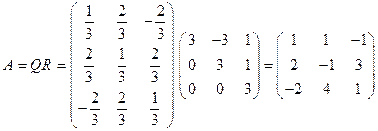






 з лінійно незалежними стовпцями
з лінійно незалежними стовпцями





 ,
, - діагональна матриця, яка утворюється з D добуванням квадратного кореня з її елементів.
- діагональна матриця, яка утворюється з D добуванням квадратного кореня з її елементів. ,
, ,
,  ,
, 






 та ж сама матриця R з процесу Грамма-Шмідта. Одержані в результаті матриці Q і R дають розклад A=QR.
та ж сама матриця R з процесу Грамма-Шмідта. Одержані в результаті матриці Q і R дають розклад A=QR.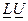 ми одержуємо ту ж матрицю А. Матрицю рангу r можна розкласти на добуток матриць розмірностей
ми одержуємо ту ж матрицю А. Матрицю рангу r можна розкласти на добуток матриць розмірностей  . У випадку, коли матриця А потребує перестановки рядків, то РА=LU і необхідна незначна зміна:
. У випадку, коли матриця А потребує перестановки рядків, то РА=LU і необхідна незначна зміна:  формується з перших r стовпців
формується з перших r стовпців  замість
замість  .
. є базисом для векторів-рядків А.
є базисом для векторів-рядків А.



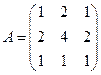



 на QR врахувавши, що перший стовпчик уже одиничний вектор.
на QR врахувавши, що перший стовпчик уже одиничний вектор. знайти ортонормований базис для векторів- стовпчиків, записати A=QR, розв’язати систему лінійних рівнянь Ax=b, якщо b=(-3,7,1,0,4).
знайти ортонормований базис для векторів- стовпчиків, записати A=QR, розв’язати систему лінійних рівнянь Ax=b, якщо b=(-3,7,1,0,4).
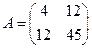
 P;
P; +…+apnbnq. При цьому матриця Аназивається лівим множником, матриця В – правим множником.
+…+apnbnq. При цьому матриця Аназивається лівим множником, матриця В – правим множником.
 = (аij)
= (аij)






