
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональне доповнення підпростору.Содержание книги
Поиск на нашем сайте
Нехай U – деякий підпростір евклідового простору Еn. Означення. Вектор а простору Еn називається ортогональним підпростору U (записують а ^U), якщо він ортогональний довільному вектору цього підпростору. Теорема 10. Для того, щоб вектор а був ортогональний підпростору U достатньо, щоб він був ортогональний кожному вектору деякого базиса цього підпростору. Означення. Підпростори U i V простору Е називаються ортогональними і позначають U^V, якщо кожний вектор u є U ортогональний кожному вектору v є V. Теорема 11. Для того, щоб підпростори U i V простору Е були ортогональними достатньо, щоб кожний вектор деякого базиса підпростору U був ортогональний кожному вектору деякого базиса підпростору V. Означення. Підпростір U^ всіх векторів простору Е, ортогональних підпростору U, називається ортогональним доповненням підпростору U. Теорема 12. Евклідів простір Еn є прямою сумою кожного свого підпростору U і його ортогонального доповнення U^: Еn=UÅ U^. Наслідок. DimEn=dimU+dim U^. Приклад. 1) Ортогоналізувати систему векторів: b1=(1,2,3,4), b2=(0,5,0,5), b3=(8,10,-8,14) Процес ортогоналізації застосовується лише до лінійно незалежної системи векторів, тому перевіримо дану систему на лінійну залежність склавши матрицю з координат даних векторів і знайдемо її ранг. A = Отже, вектори b1,b2,b3 утворюють лінійно незалежну систему векторів. За перший вектор с1 ортогональної системи візьмемо вектор b1: с1=b1=(1,2,3,4). Далі шукатимемо вектор с2 у формі лінійної комбінації векторів с1 і b2: с2=lc1+b2. Оскільки вектор c2 повинен бути ортогональним до с1, то (с1,с2)=(с1,lс1+b2)=l(c1,c1)+(c1,b2)=0 => => l=-(c1,b2)/(c1,c1)=-(1*0+2*5+3*0+4*5)/(1+4+9+16)=-1 Отже, с2=-с1+b1=(-1,3,-3,1). Вектор с3 шукатимемо у формі лінійної комбінації векторів с1,с2 і b3: с3=g1c1+g2с2+b3. Оскільки вектор с3 повинен бути ортогональним до с1,с2, то (с1,с3)=(c1,g1c1+g2с2+b3)=g1(c1,c1)+g2(c1,c2)+(c1,b3)= =g1(c1,c1)+(c1,b3)=0 (с2,с3)=(c2,g1c1+g2с2+b3)=g1(c2,c1)+g2(c2,c2)+(c2,b3)= =g2(c2,c2)+(c2,b3)=0. Звідки g1=-(с1,b3)/(c1,c1) i g2=-(с2,b3)/(c2,c2) g1=-(1*8+2*10-3*8+4*14)/(1+4+9+16)=-2 g2=-(-1*8+3*10+3*8+1*14)/(1+9+9+1)=-3 Отже, с3=-2с1-3с2+b3=-2(1,2,3,4)-3(-1,3,-3,1)+(8,10,-8,14)= (9,-3,-5,3) Одержали ортогональну систему: с1=(1,2,3,4), c2=(-1,3,-3,1), c3=(9,-3,-5,3). 2)Перевірити чи будуть вектори а1=(1,-2.2,-3) і а2=(2,-3,2,4) ортогональні, і якщо так, то доповнити систему цих векторів до ортогонального базису простору, в якому вони розглядаються. Перейти від знайденого базису до ортонормованого.
Оскільки (а1,а2)=1*2+(-2)*(-3)+2*2-3*4=0, то вектори а1,а2 ортогональні. Знайдемо тепер такий вектор х=(х1,х2,х3,х4) є Е, що (а1,х)=(а2,х)=0. Звідси одержимо СЛОР:
Загальний розв’язок системи (2х3-14х4,2х3-10х4,х3,х4),x3,x4єR Фундаментальна система розв’язків {(2,2,1,0),(-17,-10,0,1)}={x¢,x¢¢}. Вектори x¢,x¢¢ фундаментальної системи розв’язків ортогональні до векторів а1,а2 (їх знайдено з цієї умови). Якби ще вектори фундаментальної системи були ортогональними, то система векторів а1,а2, x¢,x¢¢ була б ортогональним базисом простору Е4 і залишилося б тільки пронормувати його. Але (x¢,x¢¢)¹0 і тому ортогоналізуємо спочатку систему векторів x¢,x¢¢. Згідно процесу ортогоналізації маємо с1=х1, с2=lс1+b2, де l=-(с1, x¢¢)/(c1,c1)=-(34-20)/9=6. Тоді с2=6с1+x¢¢=(-5,2,6,1). Отже, система векторів є ортогональною системою ненульових векторів. Оскільки кількість елементів цієї системи дорівнює розмірності всього простору Е4, то а1,а2,с1,с2 – ортогональний базис простору Е4. Для перетворення його в ортонормований треба кожен з векторів, що входить до базису, розділити на його норму. Знайдемо úúа2êê = Тоді
3)Знайти ортонормовану фундаментальну систему розв’язків для системи рівнянь:
Загальний розв’язок х=(2х2+2/7х4,х2,-5/7х4,х4),x4 є R.
ФСР: Ортогоналізуємо систему: b1=a1=(2,1,0,0) b2=lb2+a2 => (b1,b2)=l(b1,b1)+(b1,a2) => l=-(b1,a2)/(b1,b1)=-(2*2-1*4+0*0)/(4+1+0+0)=0 b2=a2=(2,-4,-25,-35) úúb1êê= Отже, ортонормована фундаментальна система розв’язків: 1/ 4)При яких значеннях параметра l вектори а1=(0,1,l), а2=(1,-1,1), а3=(-2,-1,l) утворюють ортогональний базис простору R. Для того, щоб вектори утворювали ортогональний базис потрібно, щоб (аi,аj) = 0. (а1,а2) = 0-1+l = 0 (а1,а3) = 0-1+l2 = 0 (а2,а3) = -2+1+l = 0
5)В евклідовому просторі F3 многочленів степеня не більше 2 над полем R зі скалярним добутком, заданим рівністю (f,g) = f3 = j1(х) = 1+2х, j2(х) = 1-5х+6х2 в цьому базисі і обчислити їх скалярний добуток двома способами:
(j1,j2) = 1. g1(x) = f1 = 1 g2(x) = lf1+f2 =l+ (g1,g 2) = 0 l = -(g1,f2)/(f2,f2)= - g2(x) = 2. a) j1 = af1+bf2+cf3 1+2x = a+b
j 1= 2f1+ b) j2 ==af1+bf2+cf2 1-5x+6x2 = a+
j2 = 1/2f1+ 3. (j1,j2) = = = = (j1,j2) = 2*1/2+ а1 = (2,1,-4), a2 = (3,5,-7), a3 = (4,-5,-6), v = (-12,9,-12). Знайдемо базис L:
Базис складається з векторів а1,а2. Ортогоналізуємо цей базис: b1 = a1 = (2,1,-4) b2 = a2-b1(a2,b1)/(b1,b1) = a2-b1(6+5+28)/(4+1+16) =a2-13/7b1 = = (3,5,-7)-13/7(2,1,-4) = 1/7(-5,22,3) Знайдемо ортогональну проекцію а даного вектора v на L: а = (v,b1)/(b1,b1)b1+(v,b2)/(b2,b2)b2 = = (-24+9+48)/(4+1+16)b1+(12*5/7+9*22/7-2*3/7):(25/49+484/49+9/7)b2 = =11/7(2,1,-4)+3/7(-5,22,3) = (1,11,-5). Знайдемо ортогональну складову b вектора v відносно L: b = v-a = (-12,9,-12)-(1,11,-5) = (-13,-2,-7).
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1680; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.11.146 (0.011 с.) |

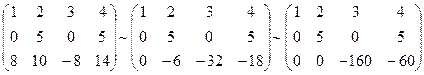 r(A)=3
r(A)=3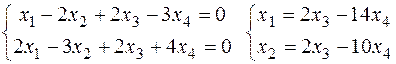
 =
= 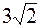 , úúа2êê=
, úúа2êê=  , úúс1êê=3, úúс2êê=
, úúс1êê=3, úúс2êê=  .
. = =
= = 
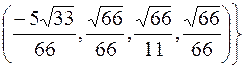 - ортонормований базис.
- ортонормований базис.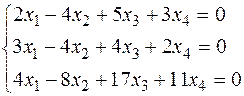
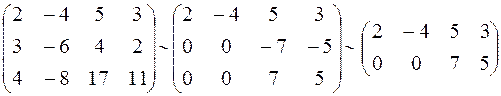
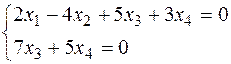

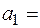 (2,1,0,0),
(2,1,0,0), 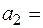 (2,-4,-25,-35)
(2,-4,-25,-35)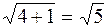 úúb2êê=
úúb2êê= 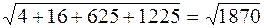
 (2,1,0,0), 1/
(2,1,0,0), 1/ 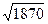 (2,-4,-25,-35).
(2,-4,-25,-35). Отже, l = 1
Отже, l = 1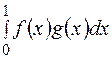 ,задані вектори f1,f2,f3. Ортогоналізувати базис f1 = 1, f2 =
,задані вектори f1,f2,f3. Ортогоналізувати базис f1 = 1, f2 = 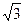 (2х-1),
(2х-1),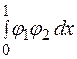 , (j1,j2) = a1b1+a2b2+a3b3
, (j1,j2) = a1b1+a2b2+a3b3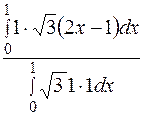 =-
=- 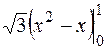 = 0
= 0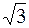 (2x-1)
(2x-1) (6x2-6x+1)
(6x2-6x+1)
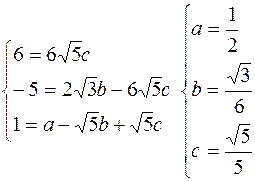
 (1+2x)(1-5x+6x2)dx =
(1+2x)(1-5x+6x2)dx = =
= =
=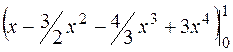 = 1-3/2-4/3+3 = 7/6
= 1-3/2-4/3+3 = 7/6



