
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двоїстість лінійного програмування.Содержание книги
Поиск на нашем сайте Лекція №1
Література: 1. Таха Х.А. Введение в исследование операций. – М.:Мир, 1985. – 496 с. 2. Мину М. Математическое программитование и алгоритмы.– М.:Наука, 1990.– 448 с. 3. Вентцель Е. С. “Исследование операций”, М. 1972 г. 4. Зайченко Ю.П. Дослідження операцій.Підручник. – К. «Слово»,2006. – 816с. 5. Зайченко О.Ю., Зайченко Ю.П. Дослідження операцій. Збірник задач. – К.: «Слово»,2007. – 472 с. 6. Заславский В.С. “Исследование операций. Сборник задач”, М.1980. – 275с. 7. Юдин Д. Б., Гольштейн Е. Г. “Линейное программирование. Задачи и методы линейного программирования ”, М. 1994, 344с.
Дослідження операцій – це наука, яка займається розробкою та практичним застосуванням методів найбільш ефективного управління організаційними системами. Предмет дослідження операцій – системи організаційного керування, які складаються з великої кількості взаємодіючих між собою підрозділів (інтереси підрозділів не завжди співпадають, можуть бути протилежними). Ціль ДСО – кількісне обгрунтування приймаємих рішень стосовно керування організацією. Основні етапи ДСО: 1. Постановка задачі. 2. Побудова математичної моделі. 3. Знаходження розв”язків. 4. Перевірка і корегування моделі. 5. Реалізація знайденого рішення на практиці. (1). Задача ставиться замовником, а операційна група конкретизує її. (2). Формалізація задачі. Цільова функція задачі (показник якості, чи ефективності системи): max E = f (x, y) (1.1) при обмеженнях gi (x, y) £ bi, i = 1, m (1.2), де х- вектор керованих змінних; у – вектор некерованих змінних; gi – функція споживання і-го ресурсу; bi – величина і-го ресурсу. (3). Для знаходження оптимального рішення задачі (1.1, 1.2) в залежності від виду і структури цільової функції та обмежень використовують відповідні методи теорії оптимальних рішень: - лінійне програмування (якщо f (x, y), gi (x, y) – лінійні функції відносно змінної х); - нелінійне програмування (якщо f (x, y), gi (x, y) – не лінійні функції відносно змінної х); - динамічне програмування (якщо цільова функція має визначену структуру (адитивна, чи мультиплікативна відносно х); - стахостичне програмування (якщо вектор у – випадковий); - дискретне програмування (якщо на змінну х накладена умова дискретності); - евристичне програмування (якщо точний оптимум знайти алгоритмічним шляхом неможливо через велику кількість варіантів).
Класи задач ДСО (за своєю постановкою): 1. Задача керування запасами. 2. Задача розподілення ресурсів. 3. Задача ремонту і заміни обладнання. 4. Задача масового обслуговування. 5. Задача теорії розкладів. 6. Задача вибору маршруту. 7. Задача планування і розміщення.
Приклади задач. 1. Транспортна задача. Маємо m пунктів виробництва. Нехай виробництво однієї продукції з обсягами виробництва за даний період часу а1, а2, …, аm. Маємо n споживачів з потребами в1, в2, …, вn. Сумарний обсяг виробництва співпадає з потребами. Вартість перевезень одиниці продукції з і-го пункту виробництва в j–й пункт споживання сі j. Завдання: скласти такий план перевезень від постачальників до споживачів, щоб всі потреби були задоволені, а сумарні витрати на перевезення – мінімальними. Розв”язок: Вводимо невідомі х іj (обсяг перевезень з і-го пункту виробництва в j–й пункт споживання. Визначаємо цільову функцію:
Визначаємо умови обмеження: Тоді повинні виконуватись такі умови:
Xij ≥ 0; (3.4)
Умова (3.3) гарантує повне вивезення продукту з усіх пунктів виробництва, а умова (3.2) – повне задоволення попиту в усіх пунктах споживання.
Матрицю
називають планом перевезень Т-задачі, а змінні xij – перевезеннями.
2. Задача про дієту. Для людини необхідно скласти харчовий раціон, який повинен включати: - білків не менше а1 гр., - вуглеводів не менше а2 гр., - мінеральних солей не менше а3 гр., - вітамінів не менше а4 гр. за добу. Нехай: - добова потреба в цих елементах – m; - маємо n видів харчових продуктів; - а іj – кількість елемента і в одиниці продукту j; - сj – ціна одиниці продукту j. Завдання: підібрати кількість харчових продуктів, які б задовольнили потребу у всіх елементах при найменших витратах. Розв”язок: Вводимо невідомі х j (кількість j–го продукту). Визначаємо цільову функцію:
Визначаємо умови обмеження: а іj х j ³ а 1
3. Задача про рюкзак. Маємо рюкзак визначеного розміру. Нехай місткість рюкзака дорівнює d. Маємо n предметів з обсягами а1, а2, …, аn. Ступінь важливості кожного продукту – с j. Виконуються умови. Завдання: вирішити які предмети покласти в рюкзак, щоб сумарна цінність була максимальна.
Висновки: - функція, яка максимізується (мінімізується) називається цільовою; - умови, яким підпорядковуються змінні, називаються обмеженнями задачі; - любий набір значень невідомих х1, х2, …, хn, хі³ 0, задовольняє всім обмеженням над допустимим розвязком задачі (сукупність всіх допустимих розвязків складає допустиму множину); - допустиме рішення, яке дає цільовій функції максимум (мінімум), називають оптимальним рішенням задачі, а саме значення цільової функції при цьому розвязкі – оптимумом. Лекція №2
Приклад:
Дані розв’язки: х1= (4, 0, 8, 1, 0); х2= (0, 1, 10, 0, 0); х3= (,,,,). Завдання: перевірити допустимість розвязків. Відповідь: х1 , х2 - допустимі розвязки, х3 - недопустимий розв’язок. Знайти значення цільової функції: f (х1) = 2 – оптимальний розв’язок; f (х2) = -7– оптимальний розв’язок.
Задачі лінійного програмування (ЗЛП). Форми ЗЛП. 1. ЗЛП з обмеженнями – рівностями (основна ЗЛП). Канонічна форма ЗЛП. Маємо: х1, х2, …, хn. Необхідно знайти такі невідємні значення цих змінних, яких би задовольняли системи лінійних рівнянь (3)
і, крім цього, обертали б в мінімум лінійну функцію: L = c1x1 + c2x2 + … cnxn ® min.
2. Симетрична форма. L = c1x1 + c2x2 + … + cnxn ® min (4.1);
Будемо вважати, що всі ці нерівності лінійно – незалежні, тобто жодне з них неможливо представити в вигляді лінійної комбінації інших. Перехід від однієї форми ЗЛП в іншу. Від задачі з обмеженнями легко перейти до ОЗЛП. Будемо вважати, що ЗЛП задана в вигляді
Будемо називати змінні у1, у2, …, ум додатковими змінними. Припустимо, що ЗЛП задана в вигляді
Таким чином виникає ЗЛП. Знайти всі відємні значення n+m змінних х1, …, хn, у1, …, уm, щоби вони задовольняли систему (4.3) і перетворювали в максимум, або в мінімум функцію (4.1). Отже, отримали ОЗЛП. Можливий і зворотній перехід. Нехай дана ЗЛП в канонічній формі, або стандартній. Введемо позначення
с = (с1, с2, …, сn) – вектор коефіцієнтів ЦФ,
Тоді задача прийме вигляд (c, x) ® max; A1x1 + A2x2 + … + Anxn ³ b, де А – вектори умов задачі при Х.
Геометричний зміст ЗЛП. Розглянемо випадок, коли число змінних (n) на два більше ніж число незалежних рівняннь (m), тобто (n – m) = 2. В такому випадку можна дві змінних, наприклад х1 та х2, обрати в якості вільних, а інші зробити базисними і виразити їх через вільні. Припустимо, що це зроблено. Отже, маємо ОЗЛП:
Дамо задачі лінійного програмування геометричну інтерпритацію: По віссям ОХ1 та ОХ2 бкдемо відкладувати значення вільних змінних х1 та х2. Візьмемо перше рівняння: х3 = a31х1 + a32х2 +b3 ³ 0 і припустимо, що х3 = 0. Тоді a31х1 + a32х2 +b3 = 0. Розвязуємо це рівняння і отримуємо рівняння кривої. Візьмемо цю криву х3 і відмітимо рисками ту сторону, де х3 > 0. Наступні криві будуємо аналогічно наведеному принципу. В результаті ми отримали (m – 2) прямих, кожна з яких визначає припустиму півплощину. Частину площини Х1ОХ2, яка належить одночасно всім цим півплощинам, утворює ОПР (область припустимих розвязків). Не важко переконатися, що ОПР утворює завжди опуклий многокутник.
Визначення: Множина точок n – вимірного євклідового простору називається опуклим, якщо разом з будь – якими двома точками цього простору воно містить також відрізок, з цими точками на кінцях. Лекція №3
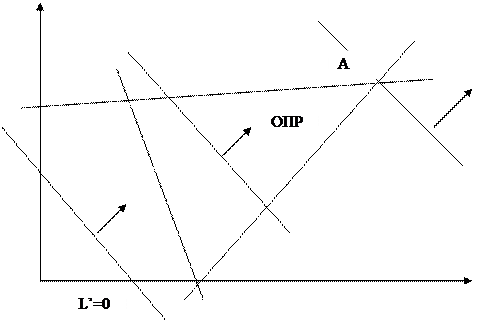
Задача. Знайти з числа припустимих оптимальний розвязок, тобто таке яке перетворює в мінімум ЦФ L = c1x1 + c2x2 + … + cnxn (5.2). Підставимо вираз (5.1) в формулу (5.2) і виразимо L як ЦФ лише вільних змінних х1 та х2. Отримаємо L = g0 + g1x1 + g2x2 (5.3). Як бачимо, рівняння (5.3) досягає мінімума при тих самих х1 та х2, що і функція L¢ = g1x1 + g2x2 (5.4). Знайдемо ці значення. Нехай L¢ = с, тоді отримаємо рівняння прямої на площині Х1ОХ2. Кутовий коефіцієнт цієї прямої дорівнює (g1 / g2), а відрізок, відрізаємий від віссі ОХ2 буде дорівнювати. Нехай маємо ОПР і пряму L¢ = 0. При переміщенні L¢ = 0 лінійна форма L* буде спадати. Отже, найменше значення вона досягне в точці А. Нехай х*1 та х*2 визначають оптимальний розвязок ЗЛП. Можна підставити їх в (5.1), знайти значення базисних змінних х*3, х*4, …, х*n, а також значення функції Lmin = g0 + g1x*1 + g2x*2.
Основні властивості ЗЛП. 1. Розвязок ОЗЛП, якщо воно існує, не може лежати внутри, а лише на її кордонах. 2. Розвязок ОЗЛП може бути не єдиним. 3. ОЗЛП може не мати навіть в випадку, коли ОПР не обмежена. 4. Розвязок ОЗЛП, мінімізуючий функцію L завжди досягається в одній з вершин многокутника припустимих розвязків. Розвязки,які лежать в одній з вершин ОПР, називається опорним, а сама вершина – опорною точкою. 5. Для того, щоб знайти оптимальний розвязок, достатньо перебрати всі вершини ОПР і обрати з них ту, де L досягає мінімума. 6. Необхідною і достатньою умовою існування розвязку ЗЛП є обмеженість ЦФ на припустимій множині.
Симплекс – метод розвязку ЗЛП. Алгоритм симплекс – методу: 1. Нехай відома деяка вершина допустимої множини. 2. Первіряємо належність цієї вершини до оптимального розвязку. Якщо так, то задача розвязана, інакше – переходимо до пункта 3. 3. Знаходиться вершина за визначеним правилом, яка краще попередньої. Переходимо до п. 2. Так як число вершин обмежено, то через кінцеве число кроків знаходимо оптимальне рішення. Симплекс – метод завжди застосовується в ЗЛП канонічної форми. Зробимо припущення: 1. Система обмежень сумісна. 2. Ранг системи дорівнює кількості рівняннь. Запишемо задачу в векторній формі
В такому випадку задачу можна поставити так: знайти розташування вектора b за векторами А1, А2, …, Аn з невідємним коефіцієнтом, щоб ЦФ досягла максимуму. Визначення: допустимий розвязок задачі (1) будемо називати опорниим, якщо вектори Аj, які відповідають додатнім його координатам, лінійно незалежні. Нульовий опорний вектор будемо вважати опорним. Базисом порного розвязку називається будь – який набір з m лінійно незалежних векторів Аj. Висновок: якщо опрне рішення містить точно m додатніх координат, то воно має єдиничний базис. В іншому випадку може бути декілько базисів. Визначення: опорний розвязок називається невиродженим, якщо він рішення містить точно m додатніх координат, інакше, розвязок – вироджений. Теорема про звязок між вершинами і опорними розвязками: вектор
Основна лема симплекс – методу. Нехай маємо m – вимірні вектори А1, А2, …, Аl, l ³ m. Ранг цієї системи дорівнює їх розмірності m і нехай вектор Аi1, Аi2, …, Аim складає базис системи векторів А1, А2, …, Аm. Замінимо один з базисних векторів Аік вектором Аs. Тоді нова система векторів буде знову базисом тоді і лише тоді, коли в розкладі As = x1sAi1 + x2sAi2 + …+ xksAik + …+ xmsAim, xks ¹ 0 (6.1).
Лекція № 4 Доведення. Необхідність: Нехай вектори з рівності (6.1) Аi1, Аi2, …, Аim знову базис і нехай вектори xks = 0 (доведення від противного). Тоді рівність (6.1) означає, що ці вектори лінійно незалежні. Маємо протиріччя. Достатність: Нехай дано xks ¹ 0. Доведемо, що вектори Аi1, Аi2, …, Аim лінійно незалежні. Припустимо, що вони лінійно залежні, тобто a1Аi1+a2Аi2+…+amАim= 0, де не всі aі дорівнюють нулю. Тоді, aк¹0, інакше б вектори Аi1, Аi2, …, Аim були б лінійно залежні. Виразимо звідси Аs:
Тоді для вектора Аs маємо два розкладення (6.1) та (6.2), причому в (6.1) коефіцієнт при Аік не дорівнює 0, а в іншому – дорівнює. Отримали протиріччя. Лема доведена.
Основні формули симплекс – методу. Нехай маємо систему векторів А1, А2, …, Аl і нехай вектори Аi1, Аi2, …, Аim складають базис. Задача: які коефіцієнти Аs будуть в новому базисі. З відношення (6.1) отримаємо
Таким чином, для вектора, який виводиться, отримаємо координати
Розглянемо координати довільного вектора Aj з розкладенням Aj = x1jAi1 + x2jAi2 + …+ xrjAir + …+ xmjAim (6.5). Підставимо в (6.5) для Air його вираз з (6.3) і отримаємо:
Отже, коефіцієнти нового базиса:
Звідси маємо, що система (6.7) – основна формула симплекс – методу, де xkj – стара координата, x¢kj – нова координата, xks – координата вводимого вектора, xrs – ведучий елемент.
Записуємо отримані дані в вигляді таблиці.
Виділимо xrs – ведучий елемент. Тоді As – ведучій стовпчик, а Air – ведуча стрічка. Нові елементи вираховуються за правилом хрест – на – хрест:
Основна теорема симплекс – методу. Нехай дана канонічна невироджена ЗЛП з слідуючою правою частиною:
Нехай дано опорний розвязок цієї задачі: `х = (`х1, `х2, …, `хm, 0,…, 0) і нехай А1, А2, …, Аm – базис цього розвязку. Тоді ЦФ буде дорівнювати f(`х) = c1`х1+ c2`х2+ …+ cm`хm. Розклад за базисом: А0= А1`х1+ А2`х2+ …+ Аm`хm. Нехай ми вирішили вектор Аs внести до базису, а Аr – вивести. Тоді: 1. Xrs ¹ 0 (за лемою); 2. Новий розвязок повинен бути допустимим.
Лекція №5
Знайдемо за основними формулами координати нового опорного розвязку в новому базисі А1, А2, …, Аm. Нехай хк0 (к = `1, `m) – координати А0 в старому базисі, х¢к0 (к = `1, `m) - координати А0 в новому базисі.
Для того, щоб новий розвязок був допустимим, необхідно щоби х¢к > 0, хr0 >0 Þ хrs > 0. Для відємних хks в формулі умова х¢к > 0 виконується автоматично. Якщо х¢к > 0, то
Для того, щоб новий розвязок був допустимим і опорним необхідне виконання двох умов: 1. хrs > 0, 2. Обираємо r, s таким чином, щоб при виконанні умов (1) і (2) новий опорний розвязок був би кращим ніж попередній. Запишемо новий опорний розвязок:
Якщо s таке, що zs – cs = ∆s < 0, то z¢s > zs, де ∆s – оцінка відповідного вектора.
Теорема 1 (про можливість отримання опорного розвязку). Якщо даний опорний розвязок такий, що серед оцінок ∆s є відємні і така, що серед хrs є хrs > 0, то ми отримаємо найкраще опорний розвязок, або замінимо вектором As такий вектор Air старого базису, для якого Домовимось, що дані, повязані з опорним розвязком, зводити до таблиці. Повна симплекс – таблиця.
В стовпчику А0 знаходяться значення невідомих даного опорного розвязку (m невідомих), інші – дорівнюють 0.
Теорема 2 (про умови оптимального опорного розвязку). Якщо для даного опорного розвязку всі оцінки ∆j ³ 0, то ций опорний розвязок - оптимальний.
Теорема 3 (про признак необмеженості ЦФ). Якщо для даного опорного розвязку існувала хоча б одна така відємна оцінка ∆s<0, для який всі Xks £0, то це означає, що ЦФ даної ЗЛП не обмежена зверху на допустимій множині.
Висновки: таким чином, в невиродженій задачі для будь – якого даного опорного розвязку виконуються або умови теореми 1, або теореми 2, або 3. Якщо конкретно виконуються умови теореми 2, чи 3, то задача розвязана. Якщо має місце умова теореми 1, то переходимо до кращого опорного розвязку. Для нього знову виконується теореми 1, 2, чи 3. Кількість різноманітних базисів обмежена. Базиси не можуть повторюватись. Таким чином, якщо задача не вироджена, то через обмежену кількість переходів (ітерацій) до кращого розвязку процес закінчиться.
Лекція № 6 Алгоритм симплекс – методу для невиродженої задачі. Дана канонічна ЗЛП:
Відомий опорний розвязок `х = (`х1, `х2, …, `хn) і його базис Аi1, Аi2, …, Аim. Для розвязку задачі необхідно розкласти за початковим базисом вектора А1, А2, …, Аn. Примітка: числа Хіо відомі. Базисні вектори розкладаються за формулою:
В = (Аі1, …, Аім). Для кожного j обчислюються оцінки
Оцінки базисних векторів завжди дорівнюють 0. Якщо всі Dj³0, то процес зупиняється. Відповідно до теореми 1, розвязок оптимальний при відємному Dj. Визначаємо присутність в такому стовпчику всіх відємних Xkj. Якщо така оцінка існує, то процес завершується. В іншому випадку, обираємо одну з відємних Dj, як правило мінімальну, і називаємо її DS. Розраховуємо відношення qк, яке дорівнює
Обираємо найменшу з них. Здійснюємо перехід до нового опорного розвязку, базис якого утворюється заміною вектора Air вектором As. Для цього обчислюємо координати всіх векторів А1, А2, …, Аn за основними формулами
Блок – схема алгоритму. 1. Обчислення xkj та Dj для початкового опорного розвязку. 2. Чи є Dj<0? (ні– (3А), так – (3Б)) 3. А) Кінець: даний опорний розвязок – оптимальний. Б) Чи є такі Dj<0, що всі xkj<0? (так – (4А), ні – (4Б)) 4. А) Кінець: задача не має розвязків. Б) Вибір вводимого в базис і виводимого вектора, тобто s i r. 5. Розрахунок нових значень xkj та Dj за основними формулами. Примітка: Теореми (2) і (3) підходять і для виродженого випадку, але там qmin=0. Через це, оцінки q розраховуються іншим способом: відповідні значенням нульові координати xrs роблять ненульовими.
Пошук початкового опорного розвязку. Простіше за все починати симплекс процес з одиничного базису. Існують спеціальні прийоми, які дозволяють звести задачу до задачі з повним одиничним базисом. Але це повязано з введенням додаткових змінних: 1) розвязок додаткової задачі; 2) метод штучного базису М. Нехай маємо канонічну ЗЛП і нехай невідомий її опорний розвязок. Змінимо її наступним чином:
де xj ³ 0, j=`1,`m; x n+1, …, x n+m – штучні змінні, а вектори А n+1, …, А n+m утворюють штучний одиничний базис; М – деяке додатнє досить велике число (вводиться для того, щоб штучні вектори вивести з базису за допомогою оцінок Dj). Ця задача називається М – задачею. Вона має явнеий опорний розвязок з одиничним базисом і до неї можна застосувати симплес метод. Припустимо, що ми розвязали М – задачу. Можливі випадки: 1. М – задача має розвязок. Нехай х*0 - її оптимальний розвязок x*0 = (х10, х20, …, хn0, x n+10, …, x n+m0), тоді розглянемо варіант a) x n+10 = …= x n+m0 =0, тобто всі штучні змінні рівні. Доведемо, що вектор х*0 – оптимальний розвязок рівняння початкової задачі. Припустимо, що це не так і що вектор `х = (`х1, `х2, …,`хn) надає значення ЦФ більше, тобто (с,`х1)> (с, х*0). Звісно, що `х = (`х1, `х2, …,`хn, 0, …, 0) припустимий розвязок М – задачі (`с,`х) = (с, `х) > (c, х*0) = (`c, х*0), так як x n+10, …, x n+m0=0. Отримана нерівність протирвічить тому, що вектор x*0 буде оптимальним розвязком М – задачі. Звідси x*0 буде оптимальним розвязком початкової задачі. б) Серед x n+10, …, x n+m0 є не нульові. Доведемо, що у цьому випадку початкова задача недопустима. Нехай це не так і вектор `х = (`х1, `х2, …,`хn) – певне допустимий розвязок початкової задачі. Розглянемо вектор `х = (`х1, `х2, …,`хn, 0, …, 0) – допустимий розвязок М – задачі і побудуємо для нього ланцюг (`с,`х) = (с, `х) > (`c, х*0) = (c, х*0) - МS x n+і0 > 0 М – як завгодно велике число, тобто маємо протиріччя, що вектор х*0 – оптимальний розвязок. М – задача не має розвязку, тобто ЦФ не обмежене зверху. У цьому випадку можна довести, що початкова задача, або недопустима, або має не обмежену ЦФ.
Розвязок М – задачі при невизначеному достатньо великому М. В М – задачі на кожній іттерації від М залежить лише оцінки Dj (Dj' М + Dj"). Так як М достатньо велике, то знак Dj співпадає зі знаком при Dj'. Звідси, не знаючи конкретного значення М ми знаємо знаки всіх оцінок Dj і можемо (різними способами) будувати симплекс – процес. Лекція №7 Примітка: 1. Якщо в початковій задачі є один, чи декілько різних одиничних векторів при умові, що праві частини невідємні, то не доцільно вводити m штучних змінних, а требо вводити їх стільки, і в тих обмеженнях, щоби ця задача мала повний одиничний базис. 2. Якщо при розвязку М – задачи будьякий штучний вектор вийшов з базису, то недоцідьно цей вектор в подальшому знову вводити в базис. Через це відповідний стовпчик в таблиці можна опустити.
Модифікований симплекс-метод. В симплекс-методі істотну роль на кожній іттерації грають оцінки
В результаті для оцінок D будемо мати Dj = сбаз В-1 Аj - cj , де В – базисна матриця, B = (Ai1, Ai2, …, Aim). Будемо тепер Dj обчислюємо в такій послідовності: L = сбаз В-1. Нехай L = (λ1, λ2, …, λm). Ці числа λі називаються симплекс – множниками для данного опорного розвязку. Припустимо, що ми знайшли всі оцінки Dj. Припустимо, що В-1 – відомо. Якщо, всі Dj ³0, то процес скінчено і розвязок – оптимальний; якщо є Dj <, то беремо з них мінімальну, нехай це буде Ds. І лише для цієї оцінки знаходимо xks
Якщо всі xks £ 0, то процес закінчується. (ЦФ – не обмежена). Якщо серед xks є додатнім, то за звичайним правилом ми знаходимо qmin і вектор, який виводять з базису. Знайшли новий базис. Якщо для нього вважаємо відому матрицю В-1, то повторюємо ці міркування. Якщо задача невироджена, чи прийняті заходи проти зациклювання, то через декілька кроків ми розвяжемо задачу. Таким чяином не потрібно обчислювати xkj для всіх aj, але для кожного опорного розвязку необхідно знати В-1 Розрахунок оберненої матриці для достатньо великої матриці досить складно. Можно обійтися без безпосереднього розвязку оберненої матриці на кожній операцій, а саме елементи зворотньої матриці для кожного опорного розвяку можно розрахувати за оберненою матрицію попереднього розвязку за основними формулами. Лекція 8 Для того, щоб впевнитись в цьому покажемо, що стовпці зворотньої матриці для данного базиса – це стовпці координат векторів Е1, Е2, …, Ем у відповідному базисі
Нехай Аі1, Аі2, …, Аім – це черговий базис і утворена матриця для даного базису дорівнює
Знайти координати вектора Еj в нашому базисі:
Так як j – довільна, то це ми довели для будьякого вектора матерь божья e1, e2, …, em Таким чином приходимо до слідуючої матриці симплекс-методу.
2 алгоритм симплекс-методу. 1. Oбчислюємо матрицю зворотню до данної базисної матриці. 2. Oбчислюємо вектор L = сбаз В-1. 3. Oбчислюємо оцінки Dj Dj = LAj-Cj. Для базисних векторів вони дорівнюють 0. Якщо всі Dj ³ 0, то опорний розвязок - оптимальний. Якщо є Dj < 0, то обираємо з них найменшу. Припустемо. Що Ds обрана. 4. Oбчислюємо xks за формулою
Якщо всі xks £ 0 і Ds < 0, то процес зупиняється (ЦФ – необмежена звеху), в іншому випадку переходимо до 5. 5. Oбчислюємо 6. За основними формулами обчислюємо новий опорний розвязок
і матрицю, обернену до нової базисної
Поветаємося до 2, маючи на увазі новий опорний розвязок. Примітка: недоліком 2 алгоритму в порівнянні з 1 є те, що необмеженість ЦФ (вона може зявитися на більш пізній іттерації при 1 алгоритмі).
Починаємо перелік за правилом критий -накритий. Отримуємо першу ітерацію.
Друга ітерація.
Третя ітерація.
ПРИКЛАД Побудувати двоїсту задачу до наступної.
Майже допустиме рішення будемо називати майже допустимим опорним рішенням (м.д.о.р.), якщо вектори аij відповідні до його ненульових координат лінійно - незалежні. Базисом м.д.о.р. будемо називати будь-який упорядочений набір із m лінійно - незалежних векторів Аj серд яких знаходяться всі вектори Аj,відповідні до всіх ненульових координат даного м.д.о.р. В основі алгоритму двоїстого симплекс методу лежать 3 теореми: Будемо розглядати тільки такі м.д.о.р. для котрих оцінки векторів Аj невід'ємна, тобто
де i1, i2, i3…im - номери базисних векторів м.д.о.р. (це відповідає тому, що вектор Сбаз В-1 є допустимим рішенням двоїстої задачі.)
СИМЕТРИЧНІ ДВОЇСТІ ЗАДАЧІ.
Двоїста для неї форма:
Отже для задачі ІІ двоїста задача ІІ":
Задачі ІІ і ІІ" складають симетричну пару двоїстих задач. Лемма та обидві теореми двоїстості є вірними і для симетричних задач, але при цьому запис другої теореми дещо змінюється. А саме, нехай дано дві задачі ІІ і ІІ" `х допустиме рішення ІІ, `y - задачі ІІ" .
`x,`y - тоді і тільки тоді будуть оптимальним рішенням, коли виконуються дві групи умов:
ДВОЇСТИЙ СИМПЛЕКС - МЕТОД. Аналогічно до звичайного симплекс - метод заключається у посідовному переході від одного n-вимірного вектора до іншого, причому правила гарантують, що через кінцеве числр кроків ми отримуємо або оптимальний вектор, або переконуємося, що задача не має границь. На відміну від симплекс методу тут послідовні вектори не мають бути допустимі, але як тільки отримуємо допустимі - вони же і оптимальні. Виявляється, що для задачі І” (якщо її привести до еквівалентної канонічної форми) двоїстою буде задача, еквівалентна до задачі І. Розв’язок задачі: В задачі на мінімум все так само, але z ' =z-Θ∆j ∆j - вибираємо максимум із додатних, тоді значення ц. ф. зменшиться. Таким чином задача І і І” складають з точністю до еквівалентності пару взаємо двоїстих задач (несиметричну пару). В матричному вигляді:
Від задачі І/ перейшли до задачі І. Лемма. Нехай Якщо для будь-яких | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

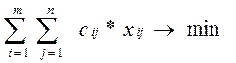
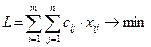 (3.1)
(3.1)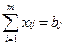 (j = 1, 2, …, n) (3.2)
(j = 1, 2, …, n) (3.2) (i = 1, 2, …, m) (3.3)
(i = 1, 2, …, m) (3.3) Х =
Х =
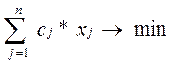


 .
.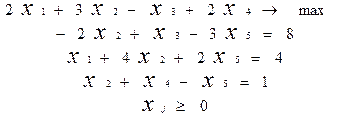

 (4.2)
(4.2)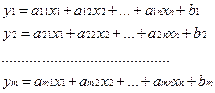 (4.3).
(4.3).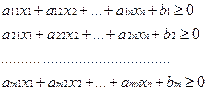
 - матриця ЗЛП,
- матриця ЗЛП,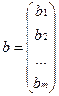 - вектор вільних членів,
- вектор вільних членів,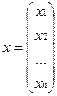 - вектор невідомих.
- вектор невідомих.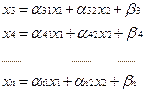 (5.1)
(5.1)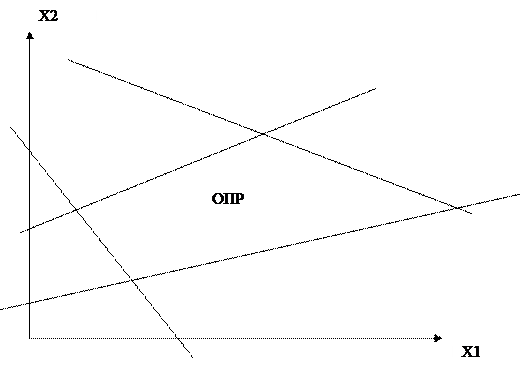
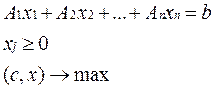 (1)
(1)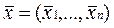 тоді і лише тоді є опорним розвязком ЗЛП, коли точка (вектор) є вершиною її допустимого многокутника.
тоді і лише тоді є опорним розвязком ЗЛП, коли точка (вектор) є вершиною її допустимого многокутника.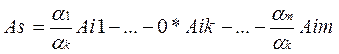 (6.2).
(6.2). (6.3).
(6.3). (6.4).
(6.4).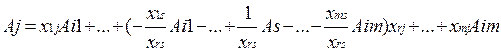 (6.6).
(6.6). (6.7)
(6.7) Ai1
Ai1
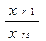


 .
.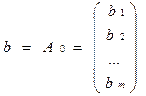 .
.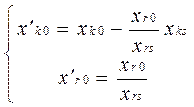 (7.1).
(7.1).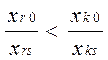 (7.2).
(7.2). .
.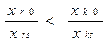 .
. .
. , де
, де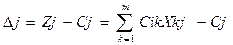 .
.
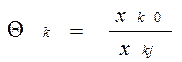 для Ñ xks > 0.
для Ñ xks > 0.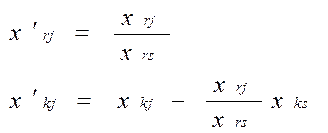 .
.
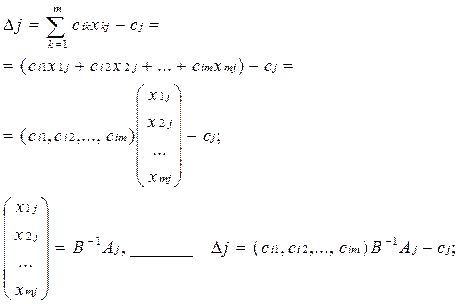
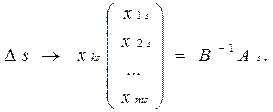
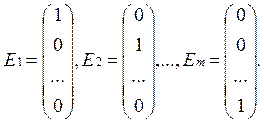
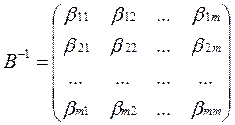
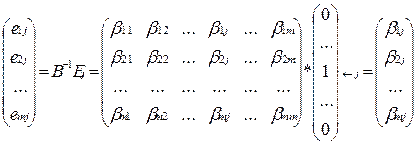

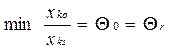
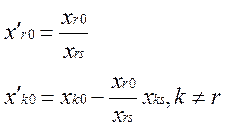
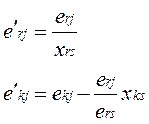
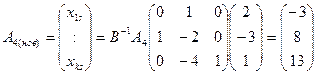
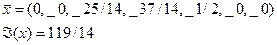


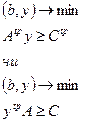
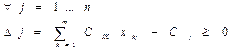
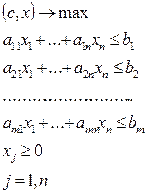
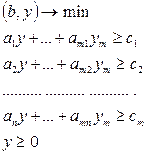
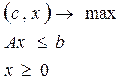
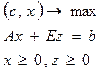
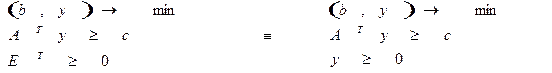
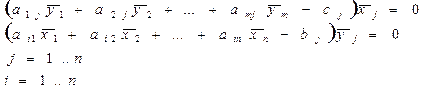
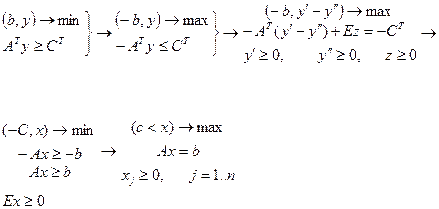
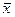 - будь-який допустимий розв’язок задачі І, а
- будь-який допустимий розв’язок задачі І, а 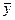 - будь-яке. Тоді виконується нерівність (с,
- будь-яке. Тоді виконується нерівність (с, 


