
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Економічна інтерпретація прямої та двоїстої задачі.Содержание книги
Поиск на нашем сайте
Оптимальне значення Ц.Ф. даної задачі ЛП можна розглядати як Zопт = ƒ(b1, b2,.., bm) Якщо оптимальний розв’язок існує і задача має хоча б один не вироджений опорний розв’язок, то справедлива теорема:
Транспортна задача лінійного програмування (в найпростішому варіанті – класична). Нехай існує m продуктів виробництва продукції i = 1..m і n пунктів споживання j =1..n. Відомо об’єми виробництва a1, a2,.., am та об’єми споживання b1,b2,.., bn. Будемо рахувати, що загальний валовий об’єм виробництва співпадає з загальним об’ємом продукції:
Відома вартість перевезення одиниці продукції від кожного пункту виробництва до кожного пункту споживання, тобто відома матриця транспортних витрат:
Де cij - вартість перевезення одиниці продукції із i-го пункту виробництва в j -тий пункт споживання. Встановити таким чином об’єм перевезення по кожному маршруту i→j, що сумарні витрати на виробництво мінімальні, а попит всіх постачальників задоволений. Введемо шукані об’єми перевезень від i-го постачальника до j-того споживача xij. Всього невідомих m x n.
c11x11 + c12x12 + … + c1nx1n + c21x21 + …+ c2nx2n + … + cmnxmn x11 + x12 + … + x1n = a1 x21 + x22 + … + x2n = a2 ………………………………….. xm1 + xm2 + … + xmn = am
x11 + x21 + … + xm1 = b1 x12 + x22 + … + xm2 = b2 …………………………………… x1n + x2n + … + xmn = bn Матрицю Х називають планом перевезень Т- задачі. А змінні xij -перевезення. Умова 3.3 гарантує повний вивіз продукту із всіх пунктів виробництва, а умова 3.2 означає повне задоволення попиту. В практиці існує як задача де виконується рівність між сумарними ресурсами і сумарним споживанням (умова балансу 3.5).
так і задача де виконується нерівність 3.6.
Задача 3.1 – 3.4 при умові 3.5 називається закритою моделлю, а при умові 3.6 – відкритою моделлю. Рівність 3.5 є необхідною і достатньою умовою сумісності систем рівнянь 3.2 і 3.3. Якщо задача являє собою відкриту модель, то вона повинна бути зведена до закритої транспортної моделі. Якщо сума
Якщо сума
Властивості транспортної задачі. 1. Транспортна завжди допустима і має оптимальний розв’язок. Нехай xij=аіbj/D, де D =∑ аі =∑bj. Доведемо, що такий набір розв’язків – допустимий розв’язок Т–задачі. Підставимо ці числа в будь-яке із М обмежень. Тоді маємо:
Доведемо обмеження допустимих множин. За умовою задачі xij ≤ min (ai). Так як кожна координата допустимого вектора обмежена, то і весь вектор буде обмеженим, тобто вся множина обмежена. На допустимій множині функція обмежена, а з цього слідує, що існує оптимальний розв’язок. 2. Ранг матриці Т-задачі r(A)= m+n-1. Якщо в Т-задачі всі цілі ai і bj, то хоча б один оптимальний розв’язок Т-задачі є цілочисленим.
Знаходження первинного опорного розв’язку Т-задачі. Метод північно-західного кута. Домовимося задавати Т-задачу наступною таблицею:
b1... bn - об’єми споживання; a1… am - об’єми виробництва. Якщо b1 < a1, то перший споживач повністю задоволений та у першого виробника залишається b1- a1 одиниць продукції. Якщо b1 > a1, то навпаки. Якщо b1 = a1, то перший споживач і перший виробник випадають. Таким чином, після заповнення північно-західної клітини випадає або один постачальник, або один споживач, або і той і інший. Закреслюємо відповідний стовпчик чи строку і корегуємо те, що залишилося. Частину таблиці, що залишилася можна вважати самостійною Т-задачею. В ній за тим самим правилом заповнюємо північно-західну клітку і т.д. Початкове число строк та стовпчиків m+n. За методом північно-західної клітини заповнюється m+n-1 клітка. Деякі клітини можуть бути заповнені нулями. Доведено, що отриманий допустимий розв’язок є опорним, причому вектори, що відповідають заповненим клітинам і складають його базис. Схема заповнення таблиці методом північно-західного кута.
А12 А21
А13 А22 А31
Метод мінімального елементу в рядках. Першою заповнюється клітина першого рядка з мінімальною вартістю перевезення. Якщо таких клітин декілька, то будемо, наприклад вибирати ту, що з ліва. Далі все аналогічно методу північно-західного кута.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.006 с.) |

 , i = 1..m
, i = 1..m







 , то необхідно ввести допоміжний пункт споживання, в якому споживання визначається:
, то необхідно ввести допоміжний пункт споживання, в якому споживання визначається: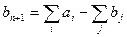
 , то вводиться допоміжний пункт виробництва. Після цього можна приступати до розв’язування задачі.
, то вводиться допоміжний пункт виробництва. Після цього можна приступати до розв’язування задачі.
 А11
А11




