
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні формули інтегруванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Із означення невизначеного інтеграла випливають такі властивості інтегрування: 1) 2) 3) 4)
Задача 1. Обчислити невизначені інтеграли методом підстановки: а) Задача2.. Обчислити невизначені інтеграли методом інтегрування частинами:
а)
1. Що таке первісна функції? Необхідна умова існування первісної. 2. Що таке невизначений інтеграл? 3. Властивості невизначеного інтегралу. 4. Правила інтегрування 5. Метод заміни змінної (підстановки) обчислення невизначених інтегралів. 6. Метод інтегрування частинами у невизначеному інтегралів.
Висновок. _________________________________________________________ __________________________________________________________________ Перевірив викладач ___________ Оцінка ___________ Дата___________ ПРАКТИЧНА РОБОТА № 14
Тема. Розв’язування задач на обчислення визначених інтегралів частинами та заміною змінних Мета роботи: Навчитись обчислювати визначені інтеграли частинами та заміною змінних. Наочне забезпечення та обладнання: 1. Інструкційні картки 2. Приклади задач 3. Роздаткові матеріали: опорні конспекти “Основні формули інтегрування” 4. Обчислювальні засоби: калькулятор.
Теоретичні відомості про правила інтегрування та застосування визначеного інтегралу. 1. Визначений інтеграл та методи його обчислення Формула Ньютона – Лейбніца. Для обчислення визначеного інтеграла від функції тобто визначений інтеграл дорівнює різниці значень первісної при верхній і нижній межах інтегрування. Метод підстановки у визначеному інтегралі. 1. Метод підстановки у визначеному інтегралі дає можливість звести інтегрування складеної функції до інтегрування табличної функції. Метод підстановки опирається на формулу диференціювання складеної функції. 2. Метод підстановки у визначеному інтегралі відрізняється від методу підстановки у невизначеному тим, що ми після обчислення інтегралу не повертаємось до старої змінної інтегрування, оскільки змінюємо межі інтегрування. Метод інтегрування частинами у визначеному інтегралі. 1. Інтегрування частинами у визначеному інтегралі базується на формулі похідної добутку:
2. Для інтегрування виразів виду:
де Р(х) – многочлен u слід приймати многочлен, що допоможе знизити його сте
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 444; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.96.95 (0.011 с.) |

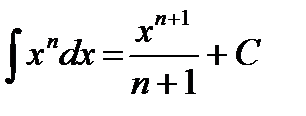 (n ¹-1), у тому числі
(n ¹-1), у тому числі ;
;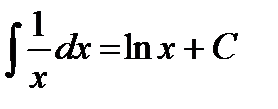 ;
;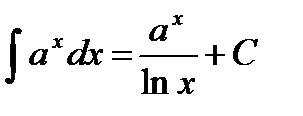 , у тому числі
, у тому числі 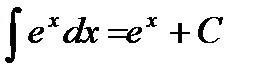 ;
;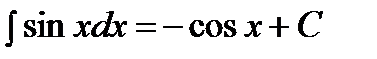 ;
; ;
;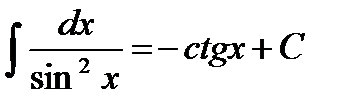 ;
;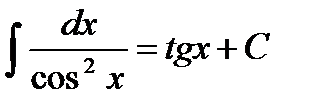 ;
; , у тому числі
, у тому числі 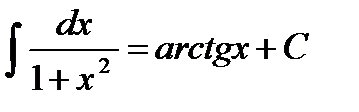 ;
;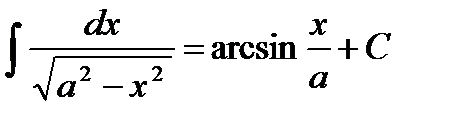 , у тому числі
, у тому числі 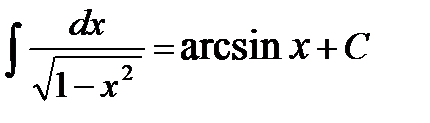 ;
;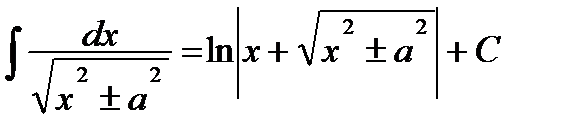 .
.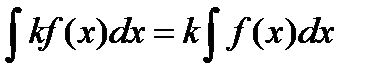 ;
; ;
;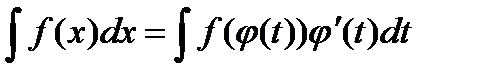 (метод заміни змінних, метод підстановки);
(метод заміни змінних, метод підстановки);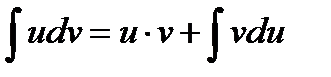 (інтегрування частинами).
(інтегрування частинами). ; б)
; б) 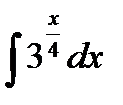 ; в)
; в) 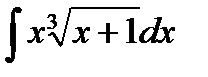 ; г)
; г) 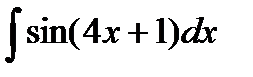 ;д)
;д) 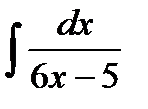
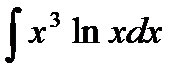 ; б)
; б) 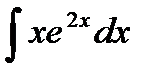 ; в)
; в) 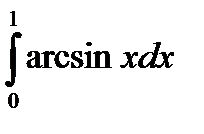
 Питання для самоконтролю знань, умінь
Питання для самоконтролю знань, умінь
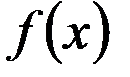 в тому випадку, коли можна знайти відповідний невизначений інтеграл
в тому випадку, коли можна знайти відповідний невизначений інтеграл  , є формула Ньютона – Лейбніца:
, є формула Ньютона – Лейбніца: 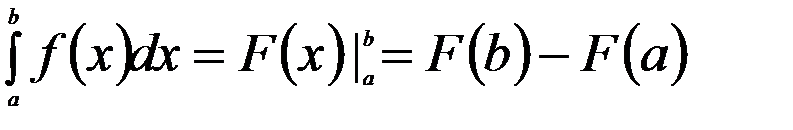 ,
,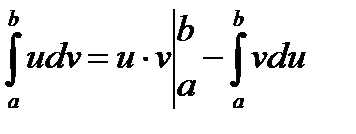
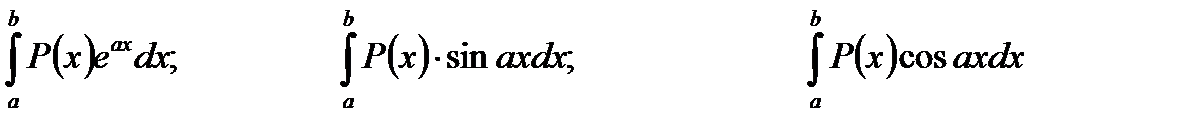 ,
,


