
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування головних геодезичних задач методом переходу на поверхню сфери (формули Бесселя)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В основі способа Бесселя лежать умови: 1) геодезична лінія 2) у відповідних точках геодезичної лінії і дуги великого кола азимути рівні;
Рис. 3.9
3) широта Цими умовами забезпечується вище поставлена вимога однозначної відповідності між геодезичною лінією на еліпсоїді і дугою великого кола на сфері. Така відповідність називається ще бесселевим зображенням. Залишається встановити зв’язки між різницею довгот 1. Вивід диференційних рівнянь, що встановлюють зв’язки між 2. Інтегрування отриманих диференційних рівнянь. При наявності всіх необхідних зв’язків між відповідними величинами на еліпсоїді і сфері головні геодезичні задачі способом Бесселя розв’язуються за наступним планом: а) перехід від елементів сфероїдного трикутника б) розв’язування геодезичних задач (прямої чи оберненої) на сфері; с) перехід від обчислених елементів сферичного трикутника, стосовно розв'язування прямої чи оберненої задачі, до відповідних елементів на еліпсоїді.
Вивід диференційних рівнянь Бесселя
Позначимо (рис. 3.9):
З цими позначеннями, прийнявши радіус сфери за одиницю, матимемо
звідки отримуємо
На основі (2.19)
отримаємо
Із (2.17) отримаємо
На основі (3.79) з врахуванням (3.80), а також помноживши чисельник і знаменник в (3.79) на
Вираз (3.81) з врахуванням (3.77) буде
звідки
На основі (3.78) і (3.82)
а, враховуючи, що
Інтегрування диференційних рівнянь Бесселя Інтегруючи диференційні рівняння (3.82) і (3.83) уздовж дуги великого кола між її точками
- еліптичні інтеграли, які в елементарних функціях не виражаються. З практичної точки зору це не є суттєвою перешкодою, поскільки можна знайти їх наближені вирази, придатні для обчислень з будь-якою, необхідною для практики, точністю. Враховуючи вимоги обчислювальної практики з використанням сучасної комп’ютерної техніки, доцільно для наближеного інтегрування рівнянь Бесселя застосувати розклад підінтегральних виразів в ряди, що швидко сходяться, з наступним почленним інтегруванням рядів. Почнемо з інтегралу (3.84). Передусім перетворимо його підінтегральну функцію, виразивши її аргумент - приведену широту – через змінну Звернемось до рис.3.10, на якому із точки Утворився прямокутний трикутник
Із прямокутного трикутника
Рис. 3.10
Тепер перетворимо рівняння (3.84)
Враховуємо, що
Введемо позначення для сталого коефіцієнта заданої геодезичної лінії в підінтегральній функції
де Тоді
Підінтегральну функцію розкладемо в ряд за формулою бінома Ньютона
Оскільки величина Замінимо синуси парних степенів через косинуси кратних дуг, на основі співвідношень:
Згрупуємо коефіцієнти при кожній функції з однаковим аргументом і введемо позначення
Тепер вираз (3.91) запишемо в вигляді
Зауважимо, що величина
В результаті інтегрування (3.94) отримаємо вираз для
Ця формула застосовується при розв’язуванні оберненої геодезичної задачі. При розв’язуванні прямої геодезичної задачі величина
За формулою (3.97) сферична відстань
після чого (3.97) запишеться в вигляді
де Наведені формули забезпечують точність обчислень 1 10-4 м в віддалі Перейдемо до обчислення інтегралу (3.85). Перед інтегруванням необхідно так перетворити підінтегральний вираз, щоб аргумент підінтегральної функції і змінна інтегрування були би одною і тією величиною. Попередньо розкладемо підінтегральну функцію в ряд за формулою бінома Ньютона і проінтегруємо перший член отриманого ряду
В підінтегральному виразі перейдемо від змінних
а згідно (3.86), для поточної точки дуги великого кола Перемноживши останні вирази, отримуємо
|
||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 570; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.25.115 (0.012 с.) |

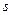 між точками
між точками  і
і  еліпсоїда (рис.3.9.а) зображується на сфері дугою
еліпсоїда (рис.3.9.а) зображується на сфері дугою  великого кола між точками
великого кола між точками  і
і  (рис.3.9.б);
(рис.3.9.б);
 будь-якої точки на сфері рівна приведеній широті відповідної точки на еліпсоїді, тобто сторони сферичного трикутника
будь-якої точки на сфері рівна приведеній широті відповідної точки на еліпсоїді, тобто сторони сферичного трикутника  і
і  відповідно рівні доповненням до
відповідно рівні доповненням до 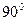 приведених широт точок
приведених широт точок  точок на еліпсоїді і аналогічною величиною
точок на еліпсоїді і аналогічною величиною 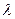 - на сфері; довжиною геодезичної лінії
- на сфері; довжиною геодезичної лінії  і
і  до елементів сферичного трикутника
до елементів сферичного трикутника  (рис. 3.9 а) і б));
(рис. 3.9 а) і б)); - нескінченно малий елемент
- нескінченно малий елемент  геодезичної лінії
геодезичної лінії  в бесселевому зображенні на сфері;
в бесселевому зображенні на сфері; 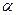 - азимут елемента
- азимут елемента  і
і  - геодезична і приведена широти точки
- геодезична і приведена широти точки  ;
;  і
і  - різниці широт і довгот точок
- різниці широт і довгот точок  ;
;  - різниця довгот точок
- різниця довгот точок  і
і  на сфері.
на сфері. (3.75)
(3.75) (3.76)
(3.76) (3.77)
(3.77) . (3.78)
. (3.78) ,
, . (3.79)
. (3.79) . (3.80)
. (3.80) , отримуємо
, отримуємо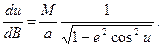 (3.81)
(3.81)
 (3.82)
(3.82) ,
, , отримуємо
, отримуємо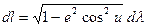 (3.83)
(3.83) (3.84)
(3.84) (3.85)
(3.85) проведено дугу великого кола перпендикулярно до продовження дуги
проведено дугу великого кола перпендикулярно до продовження дуги  .
. , катети якого
, катети якого 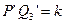 і
і  знайдуться за формулами
знайдуться за формулами (3.86)
(3.86) (3.87)
(3.87) , розглядаючи точку
, розглядаючи точку  як точку на дузі великого кола
як точку на дузі великого кола 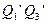 , тобто з широтою
, тобто з широтою  (3.88)
(3.88)
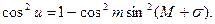 (3.89)
(3.89)
 ,
,  , де
, де  мала піввісь еліпсоїда; тоді
мала піввісь еліпсоїда; тоді
 (3.90)
(3.90)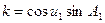 .
. . (3.91)
. (3.91)
 вміщує ексцентриситет (
вміщує ексцентриситет ( ) – малу величину, то, очевидно, що цей ряд доволі швидко сходиться.
) – малу величину, то, очевидно, що цей ряд доволі швидко сходиться. (3.92)
(3.92) (3.93)
(3.93) (3.94)
(3.94) , яка визначається за формулою (3.87), для даної геодезичної лінії величина стала; інтеграли тригонометричних функцій в рівності (3.94) обчислюються так:
, яка визначається за формулою (3.87), для даної геодезичної лінії величина стала; інтеграли тригонометричних функцій в рівності (3.94) обчислюються так:
 (3.95)
(3.95)
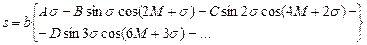 . (3.96)
. (3.96) (3.97)
(3.97)
 ,
, - номер наближення.
- номер наближення. (3.98)
(3.98)
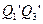
 .
. . (3.99)
. (3.99)


