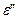Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язування сфероїдних трикутниківСодержание книги
Поиск на нашем сайте
Класичний метод побудови геодезичної мережі на земній поверхні – метод тріангуляції – складається із геометричних фігур, основними з яких є трикутники, а їхніми вершинами – геодезичні пункти. Виміряні на цих пунктах кутові та лінійні величини виправляються різного роду поправками, що враховують інструментальні похибки, вплив атмосфери тощо, а також приводяться (проектуються) на поверхню вибраного для опрацювання геодезичних вимірювань земного еліпсоїда. В результаті введення поправок у виміряні значення кутів та ліній, останні поступають на стадію математичного опрацювання з метою врівноваження і подальшого обчислення координат всіх геодезичних пунктів. Врівноваженню підлягає геодезична мережа, що складається із трикутників на еліпсоїді, які називають ще сфероїдними трикутниками. Для отримання елементів сфероїдного трикутника, переважно довжин його сторін, необхідно його розв’язати, тобто за відомими його елементами знайти невідомі (невимірювані) елементи. При класичному методі побудови геодезичних мереж задача полягає в послідовному обчисленні довжин сторін трикутників тріангуляції, причому відомими є одна сторона та кути кожного трикутника. На сучасному етапі кардинально змінилася техніка вимірювань. За допомогою GPS-технологій геодезична мережа будується як просторова побудова у вигляді своєрідного багатогранника, гранями якого є плоскі трикутники з виміряними прямолінійними відстанями між їх вершинами. Врівноваження такої просторової побудови є складним, тому більш традиційний шлях перед врівноваженням полягає в тому, що виміряні відстані редукуються на поверхню вибраного еліпсоїда. При цьому можна знайти всі кути новоутворених сфероїдних трикутників і врівноважувати мережу як лінійно-кутову. Отже, для встановлення геометричних зв’язків між трикутниками необхідно попередньо знайти величини всіх його елементів – кутів та сторін, тобто розв’язати. Враховуючи, що сторони в першокласних геодезичних мережах рідко перевищують 30 км, то трикутники тріангуляції вважаються малими сфероїдними трикутниками. Саме такі трикутники ми і будемо в подальшому розглядати. Можливість розв’язування малих сфероїдних трикутників як сферичних була розглянута в попередньому розділі (див. п.2.7.3).
Сферичний надлишок Із сферичної тригонометрії відомо, що сферичний надлишок
 сферичного трикутника будь-якого розміру сферична тригонометрія надає формули різного виду. Серед них: сферичного трикутника будь-якого розміру сферична тригонометрія надає формули різного виду. Серед них:
Рис. 3.2
В малих сфероїдних трикутниках
В результаті отримаємо наступні формули:
Для типових довжин сторін тріангуляції формули (3.2) можна використовувати без членів в дужках
У випадку вимірювання всіх кутів ці формули можна перетворити так, щоб сферичний надлишок
В першокласних геодезичних мережах сферичний надлишок Для обчислення сферичного надлишку Для рівностороннього трикутника на основі формул (3.4) можемо записати
Продиференціювавши дану формулу за змінними
Прийнявши, що Одним із основних застосувань сферичного надлишку є виявлення нев’язки
Таблиця 3.1
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.245.203 (0.009 с.) |

 сферичного трикутника
сферичного трикутника  (рис.3.2) рівний площі цього трикутника, якщо радіус сфери, на якій він розташований,
(рис.3.2) рівний площі цього трикутника, якщо радіус сфери, на якій він розташований,  . При
. При  сферичний надлишок визначається формулою
сферичний надлишок визначається формулою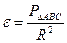 . (3.1)
. (3.1)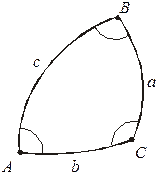
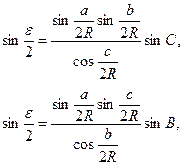

 і
і  , тому тригонометричні функції малих аргументів можна розкласти в ряди із збереженням тільки перших членів розкладів:
, тому тригонометричні функції малих аргументів можна розкласти в ряди із збереженням тільки перших членів розкладів: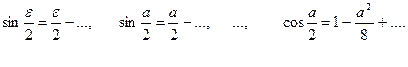
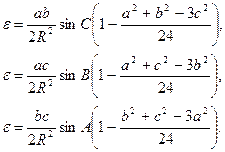 (3.2)
(3.2) (3.3)
(3.3) (3.4)
(3.4)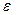 обчислюється з точністю до
обчислюється з точністю до 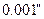 .
.
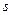 та
та 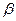 , отримаємо
, отримаємо
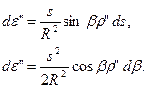
 та
та  , знайдемо допустимі похибки сторін
, знайдемо допустимі похибки сторін  і кутів
і кутів  для різних довжин сторін малого сферичного трикутника (табл. 3.1). В табл. 3.1 приведено також можливі значення сферичного надлишку
для різних довжин сторін малого сферичного трикутника (табл. 3.1). В табл. 3.1 приведено також можливі значення сферичного надлишку  у трикутнику тріангуляції
у трикутнику тріангуляції (3.5)
(3.5)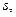 км
км
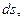 м
м