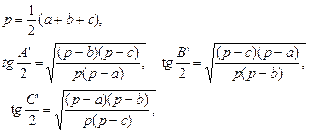Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи розв’язування малих сфероїдних трикутниківСодержание книги
Поиск на нашем сайте а) за формулами сферичної тригонометрії Розв’язування малих сфероїдних трикутників, як було вже зазначено, зводиться до розв'язування сферичних трикутників за формулами сферичної тригонометрії. Так для трикутника
де радіус сфери Недоліком даного способу є те, що сторони трикутника виражаються в частинах радіуса, а також необхідність визначати тригонометричні функції малих кутів з досить високою точністю (10-12 розрядів).
б) за теоремою Лежандра Теорема Лежандра для малих сферичних трикутників: якщо сторони плоского і сферичного трикутників відповідно рівні між собою, то кути плоского трикутника рівні кутам сферичного трикутника, зменшеними на одну третину сферичного надлишку. Нехай
Рис.3.3 Згідно теореми Лежандра, значення кутів плоского (лежандрового) трикутника буде
Сферичний надлишок Отже, якщо у сферичному трикутнику
Точність розв'язування сферичних трикутників, які можна розв’язувати за теоремою Лежандра, залежить не тільки від розмірів сторін, але і від форми трикутника. Аналізом формул встановлено, що допустимі розміри сторін трикутника знаходяться в межах від 75 до 150 км.
в) за способом аддитаментів
У попередньому способі для застосування формул плоскої тригонометрії вводилися поправки за сферичність у кути. Можливим є також спосіб використання сферичних кутів, але з введенням поправок в сторони трикутника. Розглянемо даний спосіб. Із сферичного трикутника
де Поскільки сторони сферичного трикутника є малими в порівнянні з радіусом сфери
Позначивши
і, крім того
напишемо
Або остаточно
і, аналогічно, для другої сторони
З цих формул видно, що головні члени представляють собою розв'язування сферичного трикутника як плоского, причому кути в них є сферичними. Поправочні члени Отже, якщо від вихідної сторони відняти її аддитамент і розв’язати трикутник зі сферичними кутами за формулами плоскої тригонометрії, то, додавши до знайдених довжин сторін їхні аддитаменти, отримаємо довжини сторін сферичного трикутника. Точність розв’язування малих сферичних трикутників способом аддитаментів є аналогічною, як і для розв’язування їх за теоремою Лежандра.
г) за виміряними сторонами
У випадку, коли в геодезичній мережі вимірюються лише сторони трикутників, виникає потреба обчислення горизонтальних кутів, які в подальшому можуть мати окреме застосування, наприклад, для передачі геодезичного азимута від однієї сторони до іншої. Порядок обчислень при цьому буде наступний. Виміряні між пунктами прямолінійні відстані редукують на поверхню еліпсоїда, згідно теорії редукцій геодезичних вимірювань з фізичної поверхні Землі на поверхню еліпсоїда. За знайденими таким чином сторонами
Якщо довжини сторін не перевищують 100 км, то достатньо обчислити сферичний надлишок за формулами (3.2), а потім одну третину його додати до кожного плоского кута
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 943; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 (рис. 3.2) при заданій стороні
(рис. 3.2) при заданій стороні  та кутах
та кутах  , на основі формули синусів, запишемо
, на основі формули синусів, запишемо (3.6)
(3.6) визначається як функція середньої широти
визначається як функція середньої широти  , на якій розташований трикутник, за відомими формулами
, на якій розташований трикутник, за відомими формулами  .
. - сферичний, а
- сферичний, а  - плоский трикутник, сторони якого рівні відповідним сторонам сферичного трикутника (рис. 3.3). Такий трикутник носить назву лежандровий трикутник.
- плоский трикутник, сторони якого рівні відповідним сторонам сферичного трикутника (рис. 3.3). Такий трикутник носить назву лежандровий трикутник.
 (3.7)
(3.7)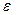 можна обчислити, наприклад, за формулами (3.4).
можна обчислити, наприклад, за формулами (3.4). і сферичні кути
і сферичні кути 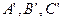 . Потім розв’язуємо трикутник за стороною
. Потім розв’язуємо трикутник за стороною 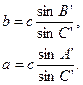 (3.8)
(3.8) (3.9)
(3.9) - шукана сторона даного сферичного трикутника.
- шукана сторона даного сферичного трикутника.

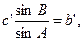

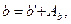 (3.10)
(3.10)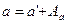 . (3.11)
. (3.11)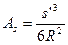 називають аддитаментами. Тому і розв'язування сферичного трикутника за формулами (3.10), (3.11) називають способом аддитаментів. Строго кажучи, аддитаментами називалися малі поправки до логарифму головного члена, коли формули виводились із застосуванням логарифмів. Хоча логарифмічні методи втратили своє значення і на практиці не застосовуються, проте в назвах окремих способів, і в тому числі при розв’язуванні сферичних трикутників, збереглися первісні терміни.
називають аддитаментами. Тому і розв'язування сферичного трикутника за формулами (3.10), (3.11) називають способом аддитаментів. Строго кажучи, аддитаментами називалися малі поправки до логарифму головного члена, коли формули виводились із застосуванням логарифмів. Хоча логарифмічні методи втратили своє значення і на практиці не застосовуються, проте в назвах окремих способів, і в тому числі при розв’язуванні сферичних трикутників, збереглися первісні терміни.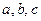 сферичного трикутника
сферичного трикутника