
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опуклість і угнутість кривих. Точки перегинуСодержание книги
Поиск на нашем сайте
Крива Крива Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої.

 
На рисунку крива опукла на Опуклість і вгнутість кривої, яка є графіком функції Інтервали опуклості і вгнутості можуть відділятися один від одного або точками, де друга похідна дорівнює нулю, або точками, де друга похідна не існує. Ці точки називаються критичними точками II роду. Якщо при переході через критичну точку II роду Правило знаходження точок перегину графіка функції 1) знайти область визначення функції; 2) знайти критичні точки II роду функції 3) дослідити знак 4) обчислити значення функції в точках перегину.
Зразки розв’язування задач Знайти точки перегину і інтервали опуклості та вгнутості графіків функцій. 1.
1) Область визначення 2) Критичні точки II роду:
а) б) 3) Знаки
Отже, на інтервалі 4)
2.
1) 2) Критичні точки II роду:
а) б) 3) Знаки
Крива опукла на інтервалах В точках 4)
3.
1) Область визначення 2) Критичні точки II роду:
а) б) 3) Знаки
Крива опукла на інтервалах В точках 4)
4.
1) Область визначення:
2) Критичні точки II роду:
а) б) Критичних точок II роду немає, графік не має точок перегину. 3) Знаки
Крива опукла на інтервалі
5.
1) Область визначення функції:
2) Критичні точки II роду:
а) б) Критичних точок немає. Отже, немає і перегинів графіка. 3) Знаки
Графік функції вгнутий на всій області визначення.
6.
1) Область визначення 2) Критичні точки II роду:
а) б) 3) Знаки
Крива опукла на інтервалі 4)
7.
1) Область визначення:
2) Критичні точки II роду:
а) б) Критичних точок немає. Отже, немає і перегинів графіка. 3) Знаки
Крива опукла на інтервалі Завдання для самостійної роботи Знайти точки перегину і інтервали опуклості та вгнутості графіків функцій. 1. 2. 3. 4. 5. Асимптоти кривих Пряма називається асимптотою кривої, якщо точка кривої необмежено наближується до неї при віддалені її від початку координат. Розрізняють вертикальні, похилі (горизонтальні) асимптоти. а) Вертикальні асимптоти. Графік функції б) Похилі асимптоти. Рівняння похилої асимптоти Слід окремо розглянути випадки, коли
Зразки розв’язування задач Знайти асимптоти кривих. 1. а) В точці Отже, б) Знайдемо похилі асимптоти:
Тоді 2. а) Область визначення функції:
В точках б) Знайдемо похилі асимптоти:
3. а) Область визначення функції:
Обчислимо Отже, б) Похилі асимптоти:
Маємо:
4. а) Область визначення функції Точок розриву II роду немає, тому графік функції не має вертикальних асимптот. б) Знайдемо похилі асимптоти:
При
5. а) Область визначення функції:
Обчислимо б) Похилих асимптот немає, тому що неможливо обчислити коефіцієнти
Завдання для самостійної роботи Знайти асимптоти кривих: 1. 2. 3. 4. 5. 6. 7.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.119.140 (0.008 с.) |

 називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі. називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.







 , вгнута на
, вгнута на  ,
,  - точка перегину.
- точка перегину. , характеризується знаком її другої похідної: якщо в деякому інтервалі
, характеризується знаком її другої похідної: якщо в деякому інтервалі  <
<  , то крива опукла на цьому інтервалі, а якщо
, то крива опукла на цьому інтервалі, а якщо  друга похідна
друга похідна  .
. . Якщо критична точка
. Якщо критична точка  є абсцисою точки перегину графіка функції;
є абсцисою точки перегину графіка функції; .
. .
. ;
;  .
. або
або  . Маємо
. Маємо  , звідки
, звідки  .
. існує на всій області визначення.
існує на всій області визначення.
 при
при  ;
;  при
при 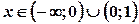 .
. крива вгнута. Враховуючи, що в точці
крива вгнута. Враховуючи, що в точці  функція неперервна, робимо висновок, що крива опукла на інтервалі
функція неперервна, робимо висновок, що крива опукла на інтервалі  . При переході через точку
. При переході через точку  друга похідна змінює знак, тому
друга похідна змінює знак, тому  .
.  - точка перегину.
- точка перегину. .
. ;
;  .
.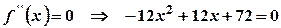 або
або  , звідки
, звідки  ,
,  .
. .
.
 і
і  , вгнута на інтервалі
, вгнута на інтервалі  .
.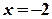 і
і  графік має перегин.
графік має перегин. .
. .
. і
і  - точки перегину.
- точки перегину. .
. ;
;
 .
. ,
,  , звідки
, звідки  .
. .
.
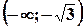 і
і  , вгнута на інтервалах
, вгнута на інтервалах  і
і  .
.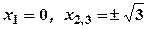 графік має перегини.
графік має перегини. .
.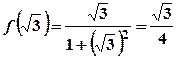 ,
, 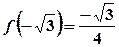 .
. - точки перегину.
- точки перегину.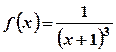 .
. .
. .
. ;
; 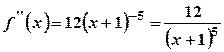 .
. .
. , але
, але  .
.
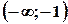 , вгнута на інтервалі
, вгнута на інтервалі  .
. .
. .
.
 .
. ;
; .
. .
.
 .
. .
. ;
;  .
.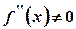 .
.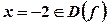 , тому
, тому 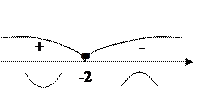
 , вгнута на інтервалі
, вгнута на інтервалі  .
. .
.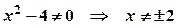 .
. .
.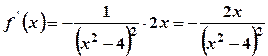 ;
;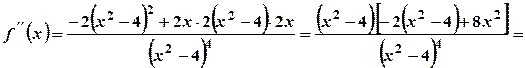
 .
. .
.
 , вгнута на інтервалах
, вгнута на інтервалах  і
і 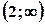 .
.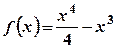 ;
; ;
;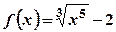 ;
;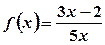 ;
; .
. має вертикальну асимптоту, якщо
має вертикальну асимптоту, якщо  або
або  ; при цьому точка
; при цьому точка  є точкою розриву II роду. Рівняння вертикальної асимптоти має вигляд
є точкою розриву II роду. Рівняння вертикальної асимптоти має вигляд  , де
, де  ,
,  , якщо ці границі існують і скінченні.
, якщо ці границі існують і скінченні.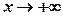 та
та  .
. .
. .
. .
. ,
,  .
. - похила асимптота.
- похила асимптота. .
.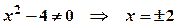 .
. .
. функція має розриви II роду, тому що
функція має розриви II роду, тому що  . Тому графік має дві вертикальні асимптоти
. Тому графік має дві вертикальні асимптоти  .
. ,
,  . Тоді
. Тоді  - горизонтальна асимптота.
- горизонтальна асимптота. .
.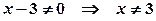 .
.
 , тому
, тому  ,
, .
. - похила асимптота.
- похила асимптота. .
. .
. ,
,  .
. (коли
(коли  ) похилої асимптоти не існує. Знайдемо
) похилої асимптоти не існує. Знайдемо  . Щоб обчислити границю, перетворимо вираз
. Щоб обчислити границю, перетворимо вираз  до вигляду
до вигляду 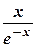 . Тоді маємо невизначеність
. Тоді маємо невизначеність  , до якої можна застосувати правило Лопіталя, а саме:
, до якої можна застосувати правило Лопіталя, а саме: 
 . Маємо:
. Маємо:  .
. .
.
 .
.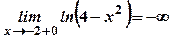 ,
, 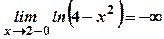 . В точках
. В точках  і
і 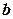 (функція не визначена при
(функція не визначена при  ).
). ;
; ;
; ;
; ;
; ;
; ;
; .
.


