
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполяція функцій сплайномСодержание книги Поиск на нашем сайте Курсова робота “ Інтерполяція функцій сплайнами”
Виконав: студент -го курсу П.І.Б
.
(місто)– 2013 ЗМІСТ
ВСТУП Сплайн-інтерполяція на сьогоднішній день є одним із найточніших методів наближення. В теорію наближень сплайни ввійшли зовсім недавно і відразу ж зайняли в ній досить важливе місце. Буквально протягом кількох років для сплайнів були розв’язані апроксимаційні задачі, на розв’язання яких для поліномів були потрачені десятиліття. З подальшим вивченням і застосуванням сплайн-функцій, знадобилося їх певне спрощення, для полегшення розрахунків. Актуальність роботи. Сьогодні сплайн-функції відіграють дуже важливу роль, вони входять в курс «Чисельні методи», як додатковий метод інтерполяції, а також використовуються в курсі «Рівняння математичної фізики» для розв’язування нерозв’язних диференціальних рівнянь; з допомогою сплайнів (в основному кубічних) розв’язуються (з великою точністю) ті задачі, які не можна розв’язати іншими, відомими, методами. Мета курсової роботи: Розглянути методи та засоби інтерполяції функції спласном, форми їх запису; формули для розрахунків інтерполяційних задач, рекурентні формули для представлення різних видів сплайнів 1-го, 2-го, 3-го та вищих порядків. З’ясувати практичність застосування сплайнів у ВНЗ при розв’язуванні задач інтерполяції. Застосувати на практиці отримані знання. Щоб досягнути зазначених вище цілей необхідно вирішити низку складних завдань, пов’язаних із повноцінним функціонуванням методів інтерполяції функції сплайнами за допомогою різних мов програмування та додатків. Об’єкт курсового дослідження: способи інтерполяції функції сплайном за допомогою мови програмування Object Pascal. Предмет дослідження: сучасні підходи до реалізації програмного коду, що виконує інтерполяцію функції сплайном. Завдання курсової роботи - визначення найпоширеніших у науці видів сплайнів та інтерполяції, виявлення основних переваг й недоліків конкретних підходів до їх реалізації; - опис сучасних підходів до використання інтерполяції: а) інтерполяція функцій сплайном третього порядку; б) апроксимація кубічними сплайнами; в) диференціювання на сітці, перехід від сітки до сітки. - визначення понять сплайна та інтерполяції та їх реалізація в математичних чисельних методах. Структура курсової роботи. Курсова робота складається зі вступу трьох розділів, висновку та списку використаної літератури. Обсяг курсової – тридцять сторінок друкованого тексту. Список літератури налічує двадцять шість найменувань.
1. МАТЕМАТИЧНІ ОСНОВИ ІНТЕРПОЛЯЦІЇ ФУНКЦІЙ ТА СПЛАЙНА 1.1. Загальні відомості про сплайни Сплайн (англ. Spline — планка, рейка) — функція, область визначення якої розбита на шматки, на кожному зі шматків функція є деяким поліномом (многочленом). В задачах інтерполяції, інтерполяція сплайном краща, ніж інтерполяція многочленом, оскільки дає схожі результати навіть при менших степенях поліномів, а також при її використанні не виникає феномена Рунге. Максимальний степінь поліномів в сплайні називається степенем сплайна. Різниця між степенем сплайна і його гладкістю називається дефектом сплайна. Сплайн (spline) називали гнучку металеву лінійку — універсальне лекало, що використовували креслярі для того, щоб гладко з'єднати окремі точки на кресленні. Тобто для графічного виконання інтерполяції. Більше того, крива, що описує деформацію гнучкої лінійки зафіксованої в окремих точках є сплайном. Отже, ми маємо фізичну модель сплайн-функції (або навпаки сплайн-функція є математичною моделлю гнучкої лінійки). Інтуїтивний підхід до використання кускових функцій в задачах апроксимації зустрічався в математиці протягом тривалого часу. Але вторгнення сплайнів в теорію наближення відбулося через задачі інтерполяції, завдяки їхнім хорошим обчислювальним та апроксимативним властивостям. Початок розвитку теорії інтерполяції сплайнами та й сам термін сплайн відраховують з 1946 року зі статті Ізо Шонберга (Isaac Jacob Schoenberg). Особливо інтенсивний її розвиток відбувся в 50-70 роки, традиційною прикладною сферою використання інтерполяційних сплайнів стали в цей час системи автоматизованого проектування. Однак потенційні можливості сплайнів значно ширші ніж просто опис деяких кривих. В реальному світі велика кількість фізичних процесів за самою своєю природою є сплайнами. В механіці це деформація гнучкої пластини чи стержня, зафіксованих в окремих точках; траєкторія руху тіла, якщо сила, що діє на нього змінюється ступінчасто (траєкторія штучного космічного об'єкта з активними та інерційними відрізками руху, траєкторія руху літака при ступінчастій зміні тяги двигунів та зміні профілю крила і т. д.). В термодинаміці це теплообмін в стержні складеному з фрагментів з різною теплопередачею. В хімії — дифузія через шари різних речовин. В електриці — поширення електромагнітних полів через різнорідні середовища. Тобто сплайн не надумана математична абстракція, а в багатьох випадках він є розв'язанням диференційних рівнянь, які описують цілком реальні фізичні процеси. Розгляд сплайнів почнемо з визначення алгебраїчного сплайна [ ]: Функція Як слідує з визначення, для побудови сплайна, що складається з Для визначення інтерполяційного сплайна з неперервною першою похідною достатньо розрахувати значення першої похідної у вузлах. Спосіб визначення похідних у вузлах сплайна визначає широку різноманітність інтерполяційних сплайнів. Часто похідні визначаються не як константи, а як деякі залежності від інтерпольованої функції та сітки інтерполяції. Якщо значення першої похідної у вузлах розраховувати виходячи з умови неперервності другої похідної (вирішуючи систему з n лінійних рівнянь) то сплайн матиме дві неперервні похідні. Такий спосіб побудови сплайна, як і сам сплайн називають глобальним, оскільки при визначенні кожного з його коефіцієнтів враховується вся множина вузлів інтерполяції. В інших випадках, для визначення окремого коефіцієнта, враховуються лише найближчі вузли інтерполяції і такі способи побудови, як і самі сплайни, називають локальними. Параметри фрагмента такого сплайна можна визначити незалежно від інших фрагментів. Найпростішою умовою побудови фрагмента локального сплайна є умова рівності полінома на кінцях відрізків відповідним значенням інтерпольованої функції.
Для найпростішого сплайна — ламаної цієї умови цілком досить. Два коефіцієнта прямої однозначно визначаються з двох рівнянь. Такий сплайн є локальним. Для поліномів вищих степенів ми повинні додати додаткові умови таким чином, щоб загальне число рівнянь дорівнювало числу коефіцієнтів полінома. Так для сплайна 3-й степені такою умовою є рівність 1-ї похідної на кінцях відрізка деякому значенню, що визначається для сусідніх відрізків однаковим чином (у формулах (2) через значення похідної функції яку наближують).
Система з 4-х рівнянь
дозволяє однозначно визначити 4 коефіцієнти полінома. Для полінома 5-ї степені ми повинні додатково накласти умову рівності 2-ї похідної на кінцях відрізка і т. д. Наведене вище показує, чому сплайн будують переважно з поліномів непарних степенів (з парною кількістю коефіцієнтів). Для поліномів парних степенів при складанні системи (3) залишається невизначеною похідна в одному з кінців відрізка і умова рівності похідних (гладкості кривої) не виконуватиметься. Тому для полінома 2-ї степені неможливо досягти рівності першої похідної в точках стику, а для 4-ї степені другої похідної і так далі, виходячи з системи рівнянь (3). Для побудови сплайнів з парними степенями штучно додають додаткові умови щоб сформувати систему рівнянь подібну (3). Коли похідні полінома сплайна визначаються як відповідні похідні інтерпольованої функції, то сплайн є ермітовим.
Існують локальні методи побудови сплайнів Бесселя та Акіми, B — сплайни []. В основному коли йде мова про сплайни то мають на увазі сплайни побудовані з алгебраїчних поліномів. Саме таких до них відноситься приведене вище визначення. Саме ці сплайни є найбільше вивченими. Проте сплайн може складатися з фрагментів функцій будь-якого класу. В [] розглянуто побудову таких сплайнів, та досліджуються їхні властивості. Автор не дає загального визначення побудованих сплайнів. Очевидно, що для довільних класів функцій з яких складається сплайн наведене на початку статті визначення не зовсім годиться. Якщо, наприклад, сплайн складається з відрізків експоненти то поняття дефекту сплайна втрачає зміст. Хоча кількість неперервних похідних залишиться важливою характеристикою. Побудова сплайна, фрагментами якого є розривні функції (раціональні функції, функції Паде) дещо виходить за рамки сплайнової ідеї, оскільки однією з основних переваг сплайнів є їхня гладкість. Якщо довільно розширювати такі конструкції, то стираються відмінності сплайнів від кускових функцій. Іншою перевагою сплайнів є ефективність обчислень. Надмірне ускладнення фрагментів суттєво знижує переваги сплайнів перед класичними функціями. Інтерполяція функцій Інтерполяція – операція наближення функції, заданої в окремих точках всередині деякого заданого проміжку. Найпростіша задача інтерполяції полягає в наступному. На відрізку [ a, b ] задано n +1 точок
У такій постановці задача інтерполяції, взагалі кажучи, може мати або незліченну безліч рішень, або зовсім не мати рішень. Однак завдання стає однозначно розв'язним, якщо замість довільної функції
Отриману інтерполяційну формулу
Лінійна інтерполяція Для вирішення системи лінійних алгебраїчних рівнянь використовувалась алгоритмічна мова Паскаль. program Spline; uses Crt, Graph; { Структура, що описує сплайн на кожному сегменті сітки} type SplineTuple=record a, b, c, d, x:real; end; const n_max=100; {Максимальний розмір масиву} var Gd,Gm: integer; {Графічний драйвер і мод} PathToDriver: string; splines: array[0..n_max-1] of SplineTuple; {Сплайн} x,y: array[0..n_max-1] of real; cur_x: real; n:integer; { Побудова сплайна } {x – вузли сітки, впорядковані за зростанням } {y – значення функції у вузлах сітки } {n – кількість вузлів сітки } Procedure BuildSpline; var i:integer; alpha:array[0..n_max-1] of real; beta:array[0..n_max-1] of real; h_i:real; h_i1:real; A:real; C:real; B:real; F:real; z:real; begin { Ініціалізація масиву сплайнів} for i:=0 to n-1 do begin splines[i].x:= x[i]; splines[i].a:= y[i]; end; splines[0].c:=0; splines[n – 1].c:=0; { Рішення системи лінійних рівнянь щодо коефіцієнтів сплайнів } { Обчислення прогоночних коефіцієнтів - прямий хід методу } alpha[0]:=0; beta[0]:=0; for i:=1 to n-2 do begin h_i:= x[i] – x[i – 1]; h_i1:= x[i + 1] – x[i]; A:= h_i; C:= 2.0 * (h_i + h_i1); B:= h_i1; F:= 6.0 * ((y[i + 1] – y[i]) / h_i1 – (y[i] – y[i – 1]) / h_i); z:= (A * alpha[i – 1] + C); alpha[i]:= -B / z; beta[i]:= (F – A * beta[i – 1]) / z; end; { Знаходження рішення - зворотний хід методу прогонки } for i:=n-2 downto 1 do splines[i].c:= alpha[i] * splines[i + 1].c + beta[i]; {По відомим коефіцієнтам c[i] знаходимо значення b[i] i d[i]} for i:=n-1 downto 1 do begin h_i:= x[i] – x[i – 1]; splines[i].d:= (splines[i].c – splines[i – 1].c) / h_i; splines[i].b:= h_i * (2.0 * splines[i].c + splines[i – 1].c) / 6.0 + (y[i] – y[i – 1]) / h_i; end; end; { Обчислення значення інтерполяційної функції у довільній точці} function Func(x:real):real; var s:SplineTuple; i,j,k:Integer; dx:real; begin if (x <= splines[0].x) then {Если x меньше точки сетки x[0]} s:= splines[1] else if (x >= splines[n – 1].x) then { Якщо x більше точки сітки x [n - 1] - користуємося останнім елементом масиву} s:= splines[n – 1] else { Інакше x лежить між граничними точками сітки, то виробляємо бінарний пошук потрібного елемента масиву} begin i:= 0; j:= n – 1; while (i + 1 < j) do begin k:= i + (j – i) div 2; if (x <= splines[k].x) then j:= k else i:= k; end; s:= splines[j]; end; dx:= (x – s.x); { Обчислення значення сплайна в заданій точці за схемою Горнера} Func:=s.a + (s.b + (s.c / 2.0 + s.d * dx / 6.0) * dx) * dx; end; begin ClrScr; Gd:=Detect; Gm:=0; PathToDriver:=''; InitGraph(gd,gm,PathToDriver); {Ініціалізуємо графіку} if GraphResult<>grok then halt; n:=16; x[0]:=0;y[0]:=260; x[1]:=20;y[1]:=260; x[2]:=40;y[2]:=300; x[3]:=60;y[3]:=270; x[4]:=80;y[4]:=330; x[5]:=100;y[5]:=230; x[6]:=120;y[6]:=250; x[7]:=140;y[7]:=220; x[8]:=160;y[8]:=210; x[9]:=180;y[9]:=170; x[10]:=200;y[10]:=150; x[11]:=220;y[11]:=230; x[12]:=240;y[12]:=180; x[13]:=260;y[13]:=190; x[14]:=280;y[14]:=220; x[15]:=300;y[15]:=150; BuildSpline; cur_x:=100; MoveTo(Round(cur_x),Round(Func(cur_x))); while (cur_x<300) do begin cur_x:=cur_x+0.1; LineTo(Round(cur_x),Round(Func(cur_x))); MoveTo(Round(cur_x),Round(Func(cur_x))); end; ReadKey; CloseGraph; END. Метод прогонки Нехай є система рівнянь, записана в матричному вигляді:
У нашому випадку згідно (1.7)
Рішення системи шукається у вигляді mi = li mi+1 + mi, i=1,...,N-1, (1.9) де Ai, Bi – прогоночні коефіцієнти. Використовуючи вираз для m i-1 із (1.9), виключимо це невідоме з i -го рівняння системи. отримуємо (ai +ci li-1)mi + bi mi+1 = di -cimi-1. Порівнюючи це співвідношення з (1.9), виводимо рекурентні формули для прогоночних коефіцієнтів li, mi (пряма прогонка): l0=m0=0, Очевидно, що mn-1=mn-1 (при сn-1=0). Всі інші невідомі знаходимо за формулами (1.9), використовуючи вирази для прогоночние коефіцієнтів (1.10). Величини li і ai +cili-1 не залежать від правої частини системи. Тому якщо обчислити їх і запам'ятати, то для вирішення систем, що відрізняються тільки правими частинами, потрібно 5 (n-1) арифметичних операцій. Код програми на Pascal #include <iostream.h> #include <math.h> #include <conio.h> #include<iomanip.h> using namespace std; const int N=5121; int main() { cout.setf(ios::left); int i, n; double max,max2,dK,oc,x1,A,B,h,x[N],a[N],b[N],c[N],d[N],y[N],mu[N],m[N],S3[N]; A=0; B=3.141592653589; max=0; max2=0; cout<<" ================="<<endl; cout<<" | n | max | d ocenka | dk |"<<endl; cout<<" -----------------------------"<<endl; for(n=5;n<=5120;n=2*n) { h=(B-A)/n; for(i=0; i<=n; i++) x[i]=A+i*h; a[0]=a[n]=1; b[0]=c[n]=0; d[0]=-sin(A); d[n]=-sin(B); for(i=1; i<n; i++) { a[i]=2*h/3; b[i]=h/6; c[i]=h/6; d[i]=(sin(x[i+1])-2*sin(x[i])+sin(x[i-1]))/h; } y[0]=-b[0]/a[0]; //прогоночні коефіціенти mu[0]=d[0]/a[0]; // прогоночні коефіціенти for(i=1; i<n; i++) //пряма прогонка { y[i]=-b[i]/(a[i]+c[i]*y[i-1]); mu[i]=(d[i]-c[i]*mu[i-1])/(a[i]+c[i]*y[i-1]); } m[n]=mu[n]; for(i=n-1; i>0; i--) m[i]=y[i]*m[i+1]+mu[i]; //Розв’язок системи for(i=1; i<=n; i++) // Визначення кінцевої формули { x1=x[i-1]+h/2; S3[i]=((x[i]-x1)*sin(x[i-1])+(x1-x[i-1])*sin(x[i]))/h+(pow((x[i]-x1),3)- h*h*(x[i]-x1))*m[i-1]/(6*h)+(pow((x1-x[i-1]),3)-h*h*(x1-x[i-1]))*m[i]/(6*h); } max=fabs(S3[1]-sin(x[0]+h/2)); // максимальна похибка for(i=1; i<=n; i++) { x1=x[i-1]+h/2; if(fabs(S3[i]-sin(x1))>max) max=fabs(S3[i]-sin(x1)); } if(n>5) { dK=max2/max; oc=max2/16; } if(n==5) cout<<" |"<<setw(8)<<n<<"|"<<setw(15)<<max<<"|"<<setw(15)<<"- "<<"|"<<setw(15)<<"-"<<"|"<<endl; if(n>5) cout<<" |"<<setw(8)<<n<<"|"<<setw(15)<<max<<"|"<<setw(15)<<oc <<"|"<<setw(15)<<dK<<"|"<<endl; max2=max; } getch(); } ВИСНОВКИ У курсовій роботі було розглянуто різні типи сплайнів та методи інтерполяції функції за їх допомогою. Було отримано програмний код прикладу використання цих методів на практиці у сфері чисельних обрахунків та наведено деякі функції, які керують роботою із сплайнами у ALGLIB. На основі всього вищевикладеного можна стверджувати, що: 1. Сплайн — функція, область визначення якої розбита на шматки, на кожному зі шматків функція є деяким поліномом (многочленом); 2. Для сплайнів є характерними такі ознаки: сплайн складається з фрагментів — функцій одного класу, які різняться лише своїми параметрами; на сусідні фрагменти в точках стикування накладаються певні умови, що зводяться до неперервності значень та деяких перших похідних. Сплайни — напрямок прикладної математики, що інтенсивно розвивається. В Internet міститься широка бібліографія щодо сплайнів (Spline Bibliography Database (SBD)); 3. Інтерполяція — спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень; 4. Існує багато різних способів інтерполяції. Вибір найпридатнішого алгоритму залежить від відповідей на питання: наскільки точний обраний метод, які затрати на його використання, наскільки гладкою є інтерполяційна функція, яку кількість точок даних вона вимагає і т.д.; 5. Основними перевагами сплайн-інтерполяції є її стійкість і мала трудомісткість. Системи лінійних рівнянь, які потрібно вирішувати для побудови сплайнів, дуже добре обумовлені, що дозволяє отримувати коефіцієнти поліномів з високою точністю. У результаті навіть про дуже великих N обчислювальна схема не втрачає стійкість. Побудова таблиці коефіцієнтів сплайна вимагає O(N) операцій, а обчислення значення сплайна в заданій точці - усього лише O(log(N)). Представлені результати широко використовуються в обчислювальній математиці. Під час виконання роботи були закріплені знання та навички використання мов Object Pascal та Java. Курсова робота “ Інтерполяція функцій сплайнами”
Виконав: студент -го курсу П.І.Б
.
(місто)– 2013 ЗМІСТ
ВСТУП Сплайн-інтерполяція на сьогоднішній день є одним із найточніших методів наближення. В теорію наближень сплайни ввійшли зовсім недавно і відразу ж зайняли в ній досить важливе місце. Буквально протягом кількох років для сплайнів були розв’язані апроксимаційні задачі, на розв’язання яких для поліномів були потрачені десятиліття. З подальшим вивченням і застосуванням сплайн-функцій, знадобилося їх певне спрощення, для полегшення розрахунків. Актуальність роботи. Сьогодні сплайн-функції відіграють дуже важливу роль, вони входять в курс «Чисельні методи», як додатковий метод інтерполяції, а також використовуються в курсі «Рівняння математичної фізики» для розв’язування нерозв’язних диференціальних рівнянь; з допомогою сплайнів (в основному кубічних) розв’язуються (з великою точністю) ті задачі, які не можна розв’язати іншими, відомими, методами. Мета курсової роботи: Розглянути методи та засоби інтерполяції функції спласном, форми їх запису; формули для розрахунків інтерполяційних задач, рекурентні формули для представлення різних видів сплайнів 1-го, 2-го, 3-го та вищих порядків. З’ясувати практичність застосування сплайнів у ВНЗ при розв’язуванні задач інтерполяції. Застосувати на практиці отримані знання. Щоб досягнути зазначених вище цілей необхідно вирішити низку складних завдань, пов’язаних із повноцінним функціонуванням методів інтерполяції функції сплайнами за допомогою різних мов програмування та додатків. Об’єкт курсового дослідження: способи інтерполяції функції сплайном за допомогою мови програмування Object Pascal. Предмет дослідження: сучасні підходи до реалізації програмного коду, що виконує інтерполяцію функції сплайном. Завдання курсової роботи - визначення найпоширеніших у науці видів сплайнів та інтерполяції, виявлення основних переваг й недоліків конкретних підходів до їх реалізації; - опис сучасних підходів до використання інтерполяції: а) інтерполяція функцій сплайном третього порядку; б) апроксимація кубічними сплайнами; в) диференціювання на сітці, перехід від сітки до сітки. - визначення понять сплайна та інтерполяції та їх реалізація в математичних чисельних методах. Структура курсової роботи. Курсова робота складається зі вступу трьох розділів, висновку та списку використаної літератури. Обсяг курсової – тридцять сторінок друкованого тексту. Список літератури налічує двадцять шість найменувань.
1. МАТЕМАТИЧНІ ОСНОВИ ІНТЕРПОЛЯЦІЇ ФУНКЦІЙ ТА СПЛАЙНА 1.1. Загальні відомості про сплайни Сплайн (англ. Spline — планка, рейка) — функція, область визначення якої розбита на шматки, на кожному зі шматків функція є деяким поліномом (многочленом). В задачах інтерполяції, інтерполяція сплайном краща, ніж інтерполяція многочленом, оскільки дає схожі результати навіть при менших степенях поліномів, а також при її використанні не виникає феномена Рунге. Максимальний степінь поліномів в сплайні називається степенем сплайна. Різниця між степенем сплайна і його гладкістю називається дефектом сплайна. Сплайн (spline) називали гнучку металеву лінійку — універсальне лекало, що використовували креслярі для того, щоб гладко з'єднати окремі точки на кресленні. Тобто для графічного виконання інтерполяції. Більше того, крива, що описує деформацію гнучкої лінійки зафіксованої в окремих точках є сплайном. Отже, ми маємо фізичну модель сплайн-функції (або навпаки сплайн-функція є математичною моделлю гнучкої лінійки). Інтуїтивний підхід до використання кускових функцій в задачах апроксимації зустрічався в математиці протягом тривалого часу. Але вторгнення сплайнів в теорію наближення відбулося через задачі інтерполяції, завдяки їхнім хорошим обчислювальним та апроксимативним властивостям. Початок розвитку теорії інтерполяції сплайнами та й сам термін сплайн відраховують з 1946 року зі статті Ізо Шонберга (Isaac Jacob Schoenberg). Особливо інтенсивний її розвиток відбувся в 50-70 роки, традиційною прикладною сферою використання інтерполяційних сплайнів стали в цей час системи автоматизованого проектування. Однак потенційні можливості сплайнів значно ширші ніж просто опис деяких кривих. В реальному світі велика кількість фізичних процесів за самою своєю природою є сплайнами. В механіці це деформація гнучкої пластини чи стержня, зафіксованих в окремих точках; траєкторія руху тіла, якщо сила, що діє на нього змінюється ступінчасто (траєкторія штучного космічного об'єкта з активними та інерційними відрізками руху, траєкторія руху літака при ступінчастій зміні тяги двигунів та зміні профілю крила і т. д.). В термодинаміці це теплообмін в стержні складеному з фрагментів з різною теплопередачею. В хімії — дифузія через шари різних речовин. В електриці — поширення електромагнітних полів через різнорідні середовища. Тобто сплайн не надумана математична абстракція, а в багатьох випадках він є розв'язанням диференційних рівнянь, які описують цілком реальні фізичні процеси. Розгляд сплайнів почнемо з визначення алгебраїчного сплайна [ ]: Функція Як слідує з визначення, для побудови сплайна, що складається з Для визначення інтерполяційного сплайна з неперервною першою похідною достатньо розрахувати значення першої похідної у вузлах. Спосіб визначення похідних у вузлах сплайна визначає широку різноманітність інтерполяційних сплайнів. Часто похідні визначаються не як константи, а як деякі залежності від інтерпольованої функції та сітки інтерполяції. Якщо значення першої похідної у вузлах розраховувати виходячи з умови неперервності другої похідної (вирішуючи систему з n лінійних рівнянь) то сплайн матиме дві неперервні похідні. Такий спосіб побудови сплайна, як і сам сплайн називають глобальним, оскільки при визначенні кожного з його коефіцієнтів враховується вся множина вузлів інтерполяції. В інших випадках, для визначення окремого коефіцієнта, враховуються лише найближчі вузли інтерполяції і такі способи побудови, як і самі сплайни, називають локальними. Параметри фрагмента такого сплайна можна визначити незалежно від інших фрагментів. Найпростішою умовою побудови фрагмента локального сплайна є умова рівності полінома на кінцях відрізків відповідним значенням інтерпольованої функції.
Для найпростішого сплайна — ламаної цієї умови цілком досить. Два коефіцієнта прямої однозначно визначаються з двох рівнянь. Такий сплайн є локальним. Для поліномів вищих степенів ми повинні додати додаткові умови таким чином, щоб загальне число рівнянь дорівнювало числу коефіцієнтів полінома. Так для сплайна 3-й степені такою умовою є рівність 1-ї похідної на кінцях відрізка деякому значенню, що визначається для сусідніх відрізків однаковим чином (у формулах (2) через значення похідної функції яку наближують).
Система з 4-х рівнянь
дозволяє однозначно визначити 4 коефіцієнти полінома. Для полінома 5-ї степені ми повинні додатково накласти умову рівності 2-ї похідної на кінцях відрізка і т. д. Наведене вище показує, чому сплайн будують переважно з поліномів непарних степенів (з парною кількістю коефіцієнтів). Для поліномів парних степенів при складанні системи (3) залишається невизначеною похідна в одному з кінців відрізка і умова рівності похідних (гладкості кривої) не виконуватиметься. Тому для полінома 2-ї степені неможливо досягти рівності першої похідної в точках стику, а для 4-ї степені другої похідної і так далі, виходячи з системи рівнянь (3). Для побудови сплайнів з парними степенями штучно додають додаткові умови щоб сформувати систему рівнянь подібну (3). Коли похідні полінома сплайна визначаються як відповідні похідні інтерпольованої функції, то сплайн є ермітовим.
Існують локальні методи побудови сплайнів Бесселя та Акіми, B — сплайни []. В основному коли йде мова про сплайни то мають на увазі сплайни побудовані з алгебраїчних поліномів. Саме таких до них відноситься приведене вище визначення. Саме ці сплайни є найбільше вивченими. Проте сплайн може складатися з фрагментів функцій будь-якого класу. В [] розглянуто побудову таких сплайнів, та досліджуються їхні властивості. Автор не дає загального визначення побудованих сплайнів. Очевидно, що для довільних класів функцій з яких складається сплайн наведене на початку статті визначення не зовсім годиться. Якщо, наприклад, сплайн складається з відрізків експоненти то поняття дефекту сплайна втрачає зміст. Хоча кількість неперервних похідних залишиться важливою характеристикою. Побудова сплайна, фрагментами якого є розривні функції (раціональні функції, функції Паде) дещо виходить за рамки сплайнової ідеї, оскільки однією з основних переваг сплайнів є їхня гладкість. Якщо довільно розширювати такі конструкції, то стираються відмінності сплайнів від кускових функцій. Іншою перевагою сплайнів є ефективність обчислень. Надмірне ускладнення фрагментів суттєво знижує переваги сплайнів перед класичними функціями. Інтерполяція функцій Інтерполяція – операція наближення функції, заданої в окремих точках всередині деякого заданого проміжку. Найпростіша задача інтерполяції полягає в наступному. На відрізку [ a, b ] задано n +1 точок
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 визначена і неперервна на відрізку
визначена і неперервна на відрізку  називається поліноміальним сплайном порядку
називається поліноміальним сплайном порядку  з вузлами
з вузлами 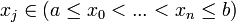 , якщо на кожному з відрізків
, якщо на кожному з відрізків  ,
,  деяка похідна
деяка похідна 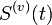 може мати розрив. Якщо в точці
може мати розрив. Якщо в точці 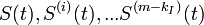 , а похідна
, а похідна  в точці
в точці  називають дефектом сплайна. Множину
називають дефектом сплайна. Множину  називають сіткою вузлів сплайна, а точки
називають сіткою вузлів сплайна, а точки  фрагмента потрібно знайти такі значення числових параметрів для кожного фрагмента — полінома степені
фрагмента потрібно знайти такі значення числових параметрів для кожного фрагмента — полінома степені  параметрів. З врахуванням умови інтерполяції та неперервності перших двох похідних визначення параметрів зводиться до розв'язання системи з
параметрів. З врахуванням умови інтерполяції та неперервності перших двох похідних визначення параметрів зводиться до розв'язання системи з  лінійних рівнянь. Як правило, значення коефіцієнтів для відрізків поліномів безпосередньо не розраховуються.
лінійних рівнянь. Як правило, значення коефіцієнтів для відрізків поліномів безпосередньо не розраховуються.



 (i = 0, 1, 2, …, n), які називаються в узлами інтерполяції, і значення деякої функції
(i = 0, 1, 2, …, n), які називаються в узлами інтерполяції, і значення деякої функції  в цих точках
в цих точках  Потрібно побудувати функцію, яка буде інтерполюватися
Потрібно побудувати функцію, яка буде інтерполюватися  , яка приймає у вузлах інтерполяції ті ж значення, що і
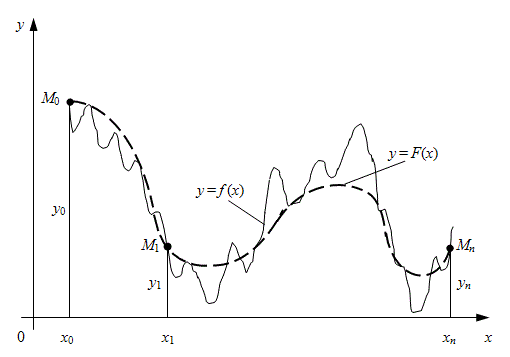
, яка приймає у вузлах інтерполяції ті ж значення, що і  Геометрично це означає (рис. 1), що потрібно знайти деяку криву
Геометрично це означає (рис. 1), що потрібно знайти деяку криву  певного типу, що проходить через заданий набір точок
певного типу, що проходить через заданий набір точок  .
.
 шукати поліном
шукати поліном  степеня не вище n, що задовольняє умовам:
степеня не вище n, що задовольняє умовам: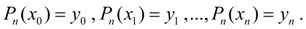 (1)
(1) використовують для наближеного обчислення значень даної функції
використовують для наближеного обчислення значень даної функції 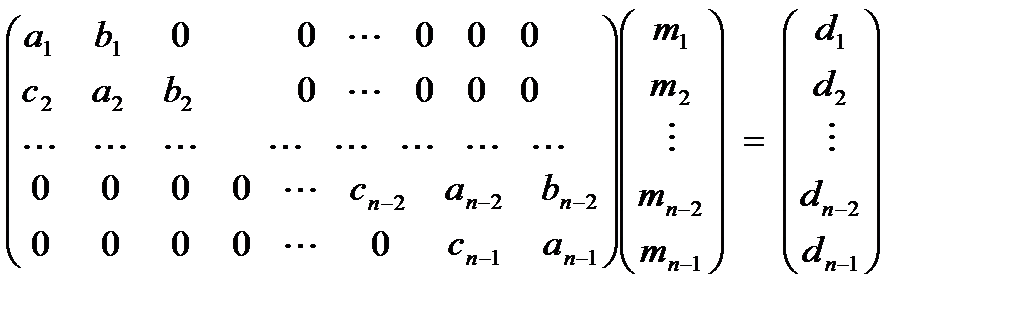 . (1.8)
. (1.8)
 . (1.10)
. (1.10)


