
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реалізація інтерполяції функції сплайнами за допомогою мови програмування object PascalСодержание книги
Поиск на нашем сайте
Лінійна інтерполяція Для вирішення системи лінійних алгебраїчних рівнянь використовувалась алгоритмічна мова Паскаль. program Spline; uses Crt, Graph; { Структура, що описує сплайн на кожному сегменті сітки} type SplineTuple=record a, b, c, d, x:real; end; const n_max=100; {Максимальний розмір масиву} var Gd,Gm: integer; {Графічний драйвер і мод} PathToDriver: string; splines: array[0..n_max-1] of SplineTuple; {Сплайн} x,y: array[0..n_max-1] of real; cur_x: real; n:integer; { Побудова сплайна } {x – вузли сітки, впорядковані за зростанням } {y – значення функції у вузлах сітки } {n – кількість вузлів сітки } Procedure BuildSpline; var i:integer; alpha:array[0..n_max-1] of real; beta:array[0..n_max-1] of real; h_i:real; h_i1:real; A:real; C:real; B:real; F:real; z:real; begin { Ініціалізація масиву сплайнів} for i:=0 to n-1 do begin splines[i].x:= x[i]; splines[i].a:= y[i]; end; splines[0].c:=0; splines[n – 1].c:=0; { Рішення системи лінійних рівнянь щодо коефіцієнтів сплайнів } { Обчислення прогоночних коефіцієнтів - прямий хід методу } alpha[0]:=0; beta[0]:=0; for i:=1 to n-2 do begin h_i:= x[i] – x[i – 1]; h_i1:= x[i + 1] – x[i]; A:= h_i; C:= 2.0 * (h_i + h_i1); B:= h_i1; F:= 6.0 * ((y[i + 1] – y[i]) / h_i1 – (y[i] – y[i – 1]) / h_i); z:= (A * alpha[i – 1] + C); alpha[i]:= -B / z; beta[i]:= (F – A * beta[i – 1]) / z; end; { Знаходження рішення - зворотний хід методу прогонки } for i:=n-2 downto 1 do splines[i].c:= alpha[i] * splines[i + 1].c + beta[i]; {По відомим коефіцієнтам c[i] знаходимо значення b[i] i d[i]} for i:=n-1 downto 1 do begin h_i:= x[i] – x[i – 1]; splines[i].d:= (splines[i].c – splines[i – 1].c) / h_i; splines[i].b:= h_i * (2.0 * splines[i].c + splines[i – 1].c) / 6.0 + (y[i] – y[i – 1]) / h_i; end; end; { Обчислення значення інтерполяційної функції у довільній точці} function Func(x:real):real; var s:SplineTuple; i,j,k:Integer; dx:real; begin if (x <= splines[0].x) then {Если x меньше точки сетки x[0]} s:= splines[1] else if (x >= splines[n – 1].x) then { Якщо x більше точки сітки x [n - 1] - користуємося останнім елементом масиву} s:= splines[n – 1] else { Інакше x лежить між граничними точками сітки, то виробляємо бінарний пошук потрібного елемента масиву} begin i:= 0; j:= n – 1; while (i + 1 < j) do begin k:= i + (j – i) div 2; if (x <= splines[k].x) then j:= k else i:= k; end; s:= splines[j]; end; dx:= (x – s.x); { Обчислення значення сплайна в заданій точці за схемою Горнера} Func:=s.a + (s.b + (s.c / 2.0 + s.d * dx / 6.0) * dx) * dx; end; begin ClrScr; Gd:=Detect; Gm:=0; PathToDriver:=''; InitGraph(gd,gm,PathToDriver); {Ініціалізуємо графіку} if GraphResult<>grok then halt; n:=16; x[0]:=0;y[0]:=260; x[1]:=20;y[1]:=260; x[2]:=40;y[2]:=300; x[3]:=60;y[3]:=270; x[4]:=80;y[4]:=330; x[5]:=100;y[5]:=230; x[6]:=120;y[6]:=250; x[7]:=140;y[7]:=220; x[8]:=160;y[8]:=210; x[9]:=180;y[9]:=170; x[10]:=200;y[10]:=150; x[11]:=220;y[11]:=230; x[12]:=240;y[12]:=180; x[13]:=260;y[13]:=190; x[14]:=280;y[14]:=220; x[15]:=300;y[15]:=150; BuildSpline; cur_x:=100; MoveTo(Round(cur_x),Round(Func(cur_x))); while (cur_x<300) do begin cur_x:=cur_x+0.1; LineTo(Round(cur_x),Round(Func(cur_x))); MoveTo(Round(cur_x),Round(Func(cur_x))); end; ReadKey; CloseGraph; END. Алгоритм побудови інтерполяційного кубічного сплайна Нехай кожному значенню аргументу xi, i=0,...,n відповідають значення функції f(xi)=yi і потрібно знайти функціональну залежність у вигляді сплайна S3(x)=аi0 +аi1(x – xi)+аi2(x – xi)2 +аi3(x – xi)3, x Î[ xi, xi+1 ] (1.1), задовольняє перерахованим нижче вимогам: 1. функція S3(xi) неперервна разом зі своїми похідними до другого порядку включно; 2. S3(xi) = yi, i=0,1,...,n; 3. S"3(x0)=S"3(xn)=0. Сформульована вище задача має єдине рішення. Друга похідна S"3(x) неперервна і, як видно з виразу (1.1), лінійна на кожному відрізку [ xi-1, xi ], (i=1,...,n), тому подамо її у вигляді
де hi = xi - xi-1, mi = S"3(xi). Інтегруючи обидві частини рівності (1.2), отримаємо
де Ai и Bi – постійні інтегрування. Нехай в (1.3) x=xi и x=xi-1, тоді використовуючи умови 2, отримаємо
З цих рівнянь знаходимо Ai і Bi, і остаточно формула (1.3) приймає вигляд
З формули (1.4) знаходимо односторонні межі похідної в точках x1,x2,...,xn-1:
Прирівнюючи вирази (1.5) і (1.6) для i=1,...,n-1, отримаємо n-1 рівняння
з n-1 невідомими mi (i=1,...,n-1). згідно з умовою (1.2) m0=mn=0. Система лінійних алгебраїчних рівнянь (1.7) має трьохдіагональну матрицю з діагональним переважанням. Такі матриці є неособливими. Тому невідомі m1 , m2 ,..., mn-1 знаходяться із системи (1.7) однозначно. Після визначення mi функція S3(x) відновлюється за формулою (1.4). Метод прогонки Нехай є система рівнянь, записана в матричному вигляді:
У нашому випадку згідно (1.7)
Рішення системи шукається у вигляді mi = li mi+1 + mi, i=1,...,N-1, (1.9) де Ai, Bi – прогоночні коефіцієнти. Використовуючи вираз для m i-1 із (1.9), виключимо це невідоме з i -го рівняння системи. отримуємо (ai +ci li-1)mi + bi mi+1 = di -cimi-1. Порівнюючи це співвідношення з (1.9), виводимо рекурентні формули для прогоночних коефіцієнтів li, mi (пряма прогонка): l0=m0=0, Очевидно, що mn-1=mn-1 (при сn-1=0). Всі інші невідомі знаходимо за формулами (1.9), використовуючи вирази для прогоночние коефіцієнтів (1.10). Величини li і ai +cili-1 не залежать від правої частини системи. Тому якщо обчислити їх і запам'ятати, то для вирішення систем, що відрізняються тільки правими частинами, потрібно 5 (n-1) арифметичних операцій. Код програми на Pascal #include <iostream.h> #include <math.h> #include <conio.h> #include<iomanip.h> using namespace std; const int N=5121; int main() { cout.setf(ios::left); int i, n; double max,max2,dK,oc,x1,A,B,h,x[N],a[N],b[N],c[N],d[N],y[N],mu[N],m[N],S3[N]; A=0; B=3.141592653589; max=0; max2=0; cout<<" ================="<<endl; cout<<" | n | max | d ocenka | dk |"<<endl; cout<<" -----------------------------"<<endl; for(n=5;n<=5120;n=2*n) { h=(B-A)/n; for(i=0; i<=n; i++) x[i]=A+i*h; a[0]=a[n]=1; b[0]=c[n]=0; d[0]=-sin(A); d[n]=-sin(B); for(i=1; i<n; i++) { a[i]=2*h/3; b[i]=h/6; c[i]=h/6; d[i]=(sin(x[i+1])-2*sin(x[i])+sin(x[i-1]))/h; } y[0]=-b[0]/a[0]; //прогоночні коефіціенти mu[0]=d[0]/a[0]; // прогоночні коефіціенти for(i=1; i<n; i++) //пряма прогонка { y[i]=-b[i]/(a[i]+c[i]*y[i-1]); mu[i]=(d[i]-c[i]*mu[i-1])/(a[i]+c[i]*y[i-1]); } m[n]=mu[n]; for(i=n-1; i>0; i--) m[i]=y[i]*m[i+1]+mu[i]; //Розв’язок системи for(i=1; i<=n; i++) // Визначення кінцевої формули { x1=x[i-1]+h/2; S3[i]=((x[i]-x1)*sin(x[i-1])+(x1-x[i-1])*sin(x[i]))/h+(pow((x[i]-x1),3)- h*h*(x[i]-x1))*m[i-1]/(6*h)+(pow((x1-x[i-1]),3)-h*h*(x1-x[i-1]))*m[i]/(6*h); } max=fabs(S3[1]-sin(x[0]+h/2)); // максимальна похибка for(i=1; i<=n; i++) { x1=x[i-1]+h/2; if(fabs(S3[i]-sin(x1))>max) max=fabs(S3[i]-sin(x1)); } if(n>5) { dK=max2/max; oc=max2/16; } if(n==5) cout<<" |"<<setw(8)<<n<<"|"<<setw(15)<<max<<"|"<<setw(15)<<"- "<<"|"<<setw(15)<<"-"<<"|"<<endl; if(n>5) cout<<" |"<<setw(8)<<n<<"|"<<setw(15)<<max<<"|"<<setw(15)<<oc <<"|"<<setw(15)<<dK<<"|"<<endl; max2=max; } getch(); }
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 402; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.181.194 (0.006 с.) |

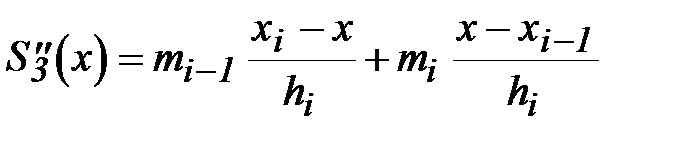 , (1.2)
, (1.2) , (1.3)
, (1.3) , i=1,...,n.
, i=1,...,n.
 . (1.4)
. (1.4) , (1.5)
, (1.5)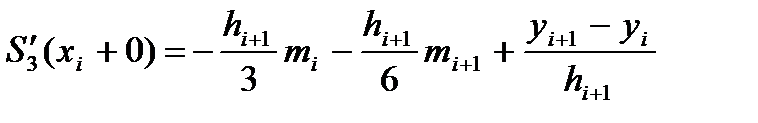 . (1.6)
. (1.6) (1.7)
(1.7)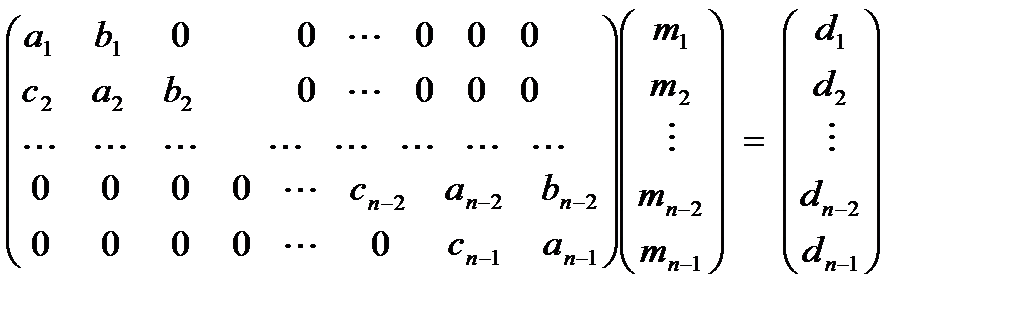 . (1.8)
. (1.8)
 . (1.10)
. (1.10)


