
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості допустимої множини та множини розв’язків задачі лінійного програмуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введемо деякі означення, пов’язані з поняттям опуклості. Розглянемо в Відрізком в Множина точок
називається півпростором в Множина точок
називається гіперплощиною в Непорожня множина Лема 1.3.1. Перетин опуклих множин — опукла множина (якщо тільки вона непорожня). Доведення. Нехай Теорема 1.3.1. Допустима множина ЗЛП опукла (якщо вона непорожня). Доведення. Оскільки допустима множина Окремим обмеженням ЗЛП може бути або гіперплощина, або півпростір. Нехай Тоді для будь-якої точки
тобто Аналогічно для півпростору. Нехай
тобто Теорема 1.3.2. Множина оптимальних точок допустимої множини ЗЛП опукла (якщо вона непорожня). Доведення. Якщо оптимальна точка єдина, то теорема вірна в силу нашої умови вважати опуклою множину, що складається з однієї точки. Нехай оптимальних точок більше ніж одна. Візьмемо дві з них, Нехай Розглянемо будь-яку точку Тоді
Отже, З теореми 1.3.2 випливає, що множина оптимальних точок не може бути скінченною, якщо оптимальна точка не єдина. Теорема 1.3.3. Якщо цільова функція ЗЛП на максимум (мінімум) обмежена зверху (знизу) на допустимій множині, то ця задача має оптимальний розв’язок. Назвемо тепер многогранною множиною перетин скінченого числа півпросторів. Обмежена многогранна множина називається многогранником. Очевидно, що допустима область Вершиною опуклого многогранника у просторі Тобто Лема 1.3.2. Будь-яка точка опуклого обмеженого многогранника є опуклою лінійною комбінацією його вершин. Тобто, якщо
Теорема 1.3.4. Якщо допустима множина Доведення. Нехай Припустимо, що
Нехай
Далі
де З (1.3.1) випливає, що Теорему доведено. Розглянута властивість дає важливу ідею розв’язування ЗЛП — перебір вершин її допустимої множини. Але такий шлях розв’язування ЗЛП, навіть з відносно невеликим числом обмежень і невідомих, практично нездійсненний, оскільки процес відшукування вершин досить трудомісткий, а число вершин многогранника може бути досить великим. Тому на початку 50-х років було винайдено американським математиком Дж.Данцигом досить раціональний спосіб перебору вершин: симплекс-метод або метод послідовного поліпшення плану для розв’язування задач лінійного програмування [14]. Нехай розглядається задача з непорожньою допустимою множиною. Загальна ідея симплекс-методу: 1) тим чи іншим способом знаходиться одна з вершин допустимої області 2) по певному правилу перевіряється, чи не можна стверджувати, що задача не має оптимальних розв’язків (цільова функція необмежена зверху або, відповідно, знизу на допустимій множині); якщо стверджувати це можна, то задача нерозв’язувана; якщо не можна, то 3) по певному правилу шукаємо нову, ліпшу з точки зору значення цільової функції вершину і повертаємося на 1-й крок. Далі розглянемо строге обгрунтування симплекс-методу для невироджених задач лінійного програмування. Симплекс-метод
|
||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1045; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.006 с.) |

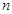 -мірному евклідовому просторі
-мірному евклідовому просторі 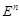 дві точки
дві точки  та
та 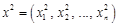 .
.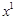 і
і  назвемо множину всіх точок
назвемо множину всіх точок 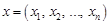 таких, що
таких, що  , де
, де 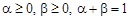 ,
, 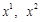 — кінці відрізка. Будемо його позначати
— кінці відрізка. Будемо його позначати 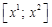 .
. , яка задовольняє умові
, яка задовольняє умові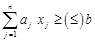 ,
,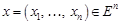 , яка задовольняє умові
, яка задовольняє умові ,
,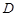 називається опуклою, якщо для будь-яких
називається опуклою, якщо для будь-яких  відрізок
відрізок 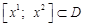 . Тобто разом з будь-якими двома точками, що належать множині, цій множині належать і усі точки відрізка, що з’єднує дані точки. Якщо множина складається з однієї точки, то умовимося, що ця множина опукла.
. Тобто разом з будь-якими двома точками, що належать множині, цій множині належать і усі точки відрізка, що з’єднує дані точки. Якщо множина складається з однієї точки, то умовимося, що ця множина опукла.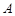 і
і 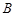 — опуклі множини і
— опуклі множини і  . Тоді
. Тоді 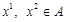 і
і 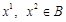 . З означення опуклої множини
. З означення опуклої множини  і
і 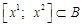 . Отже
. Отже  , а це і означає, що
, а це і означає, що 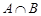 — опукла множина.
— опукла множина.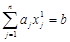 і
і 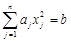 .
.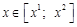
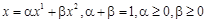 ,
,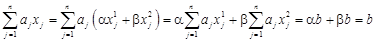 ,
, належить гіперплощині.
належить гіперплощині.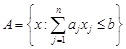 і
і 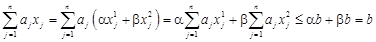 ,
,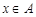 і
і 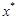 і
і  .
.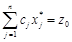 і
і  — оптимальне значення цільової функції.
— оптимальне значення цільової функції.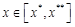 :
:  . Очевидно, що
. Очевидно, що 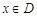 .
.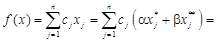
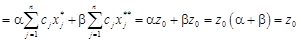 .
.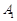 — многогранна множина. Надалі область
— многогранна множина. Надалі область 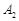 називається будь-яка точка, яка не є внутрішньою точкою ніякого відрізка, що цілком належить цьому многограннику.
називається будь-яка точка, яка не є внутрішньою точкою ніякого відрізка, що цілком належить цьому многограннику.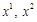 таких що
таких що  ,
,  і
і  , де
, де 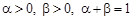 .
.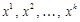 — вершини многогранника
— вершини многогранника  .
.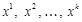 — вершини допустимого многогранника
— вершини допустимого многогранника 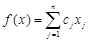 за умови
за умови  . Тоді
. Тоді .
.
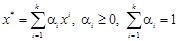 .
. ,
,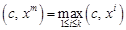 .
.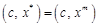 , а це і означає, що існує вершина
, а це і означає, що існує вершина 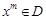 , у якій цільова функція
, у якій цільова функція 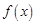 набуває найбільшого значення.
набуває найбільшого значення.


