
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двоетапний метод штучного базису.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай маємо КЗЛП:
Розглянемо допоміжну КЗЛП:
або у матричному вигляді
де Цільову функцію цієї задачі можна розглядати як міру недопустимості при перевірці виконання обмежень задачі. Коли Нехай, як і раніше, Розв’язуємо задачу (1.5.2) симплекс-методом з початковим базисним розв’язком Оскільки а) Отже, оптимальний базисний розв’язок допоміжної КЗЛП має вигляд:
Оскільки Отже, вектор б) Доведемо, що у цьому випадку початкова задача (1.5.1) не має жодного розв’язку (допустима множина порожня). Доведемо це від супротивного. Нехай Тоді Але при цьому Приклад 1.12. Розв’язати ЗЛП:
Побудуємо допоміжну ЗЛП:
Приймемо за початковий базисний розв’язок Таблиця 1.15.
Отже, оптимальний розв’язок задачі (1.5.4) є Для побудови початкової симплекс-таблиці задачі (1.5.3) скористаємося останньою частиною таблиці (1.15), але замінимо елементи стовпчика Таблиця 1.16.
Оскільки всі оцінки невід’ємні, то початковий базисний розв’язок виявляється і оптимальним для ЗЛП (1.5.3):
Цей метод носить назву двоетапного методу штучного базису. Він дозволяє знайти оптимальний розв’язок початкової задачі у два етапи. На першому етапі розв’язується допоміжна КЗЛП (1.5.2) з одиничним базисом. Якщо до базису, який відповідає оптимальному розв’язку допоміжної задачі, не входять штучні вектори, тоді цей базисний розв’язок приймається за початковий для задачі (1.5.1). На другому етапі розв’язуємо симплекс-методом задачу (1.5.1). Якщо до оптимального базису задачі (1.5.2) входять штучні вектори, тоді задача (1.5.1) буде нерозв’язуваною. Існує інший метод, який дозволяє одночасно з пошуком початкового базисного розв’язку знайти її оптимум. Це – М-метод. 2. М-метод розв’язування КЗЛП. Нехай маємо КЗЛП (1.5.1) з Як і у двоетапному методі штучного базису, який розглядався вище, в систему обмежень вводимо штучні змінні для отримання повного одиничного базису. Але при цьому цільова функція будується інакше. Допоміжна М-задача має вигляд:
де За використання штучних змінних в обмеженнях задачі вводиться великий штраф у вигляді коефіцієнту М-задача розв’язується симплекс-методом з однією особливістю, яка пов’язана з коефіцієнтами
У симплекс-таблиці вводяться два рядка для запису Розв’язуючи КЗЛП (1.5.5), можна отримати три варіанта відповіді:
а) у оптимальному розв’язку М-задачі В цьому випадку оптимальним розв’язком початкової задачі (1.5.1) є вектор Дійсно, нехай Оскільки
де Нерівність б) у оптимальному розв’язку М-задачі хоча б одна із штучних координат В цьому випадку можна довести, що початкова задача не має жодного допустимого розв’язку ( в) при достатньо великих Зауважимо, що у М-методі, константі Для розв’язування М-задачі з використанням ЕОМ можна брати за Приклад 1.13.
Побудуємо М-задачу:
Початковий базис М-задачі складається з штучних одиничних векторів Розв’язування М-задачі наведено у таблиці 1.17. Таблиця 1.17
Зручно записувати оцінку у такому вигляді Оцінка
Оцінки
Таблиця 1.18.
Вибираємо Таблиця 1.19.
Оскільки всі Таблиця 1.20.
Оцінка Зауваження. Якщо в КЗЛП є одиничні вектори, але їх не вистачає для формування базису, тоді в задачу вводиться стільки штучних змінних, скільки не вистачає одиничних векторів. Причому вибір обмежень, в які вводяться штучні змінні, визначається структурою одиничних векторів, яких не вистачає. (В усіх базисних одиничних векторах одиниці мають стояти на різних місцях.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.237.52 (0.011 с.) |

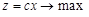 ,
,
 ,
де
,
де  .
.
 ,
,
 ,
,
 ,
…
,
…
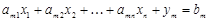 ,
,
 .
.
 ,
,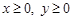 ,
, — одинична матриця розміру
— одинична матриця розміру 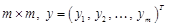 .
. , тоді
, тоді 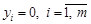 . Тому оптимальний базисний розв’язок цієї задачі буде допустимим для задачі (1.5.1).
. Тому оптимальний базисний розв’язок цієї задачі буде допустимим для задачі (1.5.1). — допустима множина початкової КЗЛП (1.5.1), а
— допустима множина початкової КЗЛП (1.5.1), а  — допустима множина допоміжної КЗЛП (1.5.2) і нехай
— допустима множина допоміжної КЗЛП (1.5.2) і нехай  .
. та з одиничним базисом
та з одиничним базисом 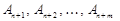 (за умовою всі
(за умовою всі  ).
). , то можливі два випадки:
, то можливі два випадки: . Це можливо тоді і тільки тоді, якщо всі
. Це можливо тоді і тільки тоді, якщо всі  .
. .
. — базисний розв’язок, то серед
— базисний розв’язок, то серед  , не більше
, не більше 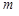 відмінних від нуля.
відмінних від нуля. і буде допустимим базисним розв’язком задачі (1.5.1).
і буде допустимим базисним розв’язком задачі (1.5.1). . Це можливо лише у тому випадку, коли хоча б одна з компонент
. Це можливо лише у тому випадку, коли хоча б одна з компонент  оптимального базисного розв’язку додатна (відмінна від нуля).
оптимального базисного розв’язку додатна (відмінна від нуля). допустимий (не обов’язково базисний) розв’язок початкової КЗЛП (1.5.1),
допустимий (не обов’язково базисний) розв’язок початкової КЗЛП (1.5.1),  .
. — допустимий розв’язок допоміжної КЗЛП (1.5.2) (
— допустимий розв’язок допоміжної КЗЛП (1.5.2) ( ).
). , що суперечить тому, що
, що суперечить тому, що  ,
,
 ,
,
 ,
,
 .
.
 ,
,
 ,
,
 ,
,
 .
.
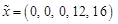 з базисом
з базисом  . Розв’яжемо задачу (1.5.4) (табл. 1.15):
. Розв’яжемо задачу (1.5.4) (табл. 1.15):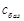
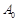
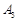
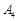

 . Серед базисних векторів немає штучних. Таким чином, вектор
. Серед базисних векторів немає штучних. Таким чином, вектор  є початковим базисним розв’язком задачі (1.5.3). Його базис складають вектори
є початковим базисним розв’язком задачі (1.5.3). Його базис складають вектори  .
. відповідно до даних цільової функції задачі (1.5.3) (табл. 1.16).
відповідно до даних цільової функції задачі (1.5.3) (табл. 1.16). .
.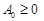 .
. ,
,
 — достатньо велике число.
— достатньо велике число. у цільовій функції при штучних змінних.
у цільовій функції при штучних змінних. записуються у вигляді:
записуються у вигляді: .
. та
та  . Розв’язування М-задачі ведеться по рядку оцінок
. Розв’язування М-задачі ведеться по рядку оцінок  , а потім по рядку
, а потім по рядку  всі
всі  .
. .
. — довільний допустимий розв’язок задачі (1.5.1). Тоді
— довільний допустимий розв’язок задачі (1.5.1). Тоді  — допустимий розв’язок задачі (1.5.5).
— допустимий розв’язок задачі (1.5.5). — оптимальний розв’язок задачі (1.5.5), то маємо
— оптимальний розв’язок задачі (1.5.5), то маємо
 .
. і доводить оптимальність
і доводить оптимальність  .
.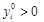 .
.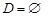 ).
). . Тоді і початкова задача нерозв’язувана, тобто
. Тоді і початкова задача нерозв’язувана, тобто  .
. .
. ,
, ,
, ,
,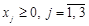 .
. ,
, ,
, ,
, 
 .
.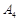 (при штучній змінній
(при штучній змінній  ) та
) та  (при штучній змінній
(при штучній змінній  ). Початковий базисний розв’язок
). Початковий базисний розв’язок  .
.
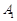
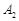

 .
. . Значить
. Значить  , а
, а  .
. ,
,  ,
,  .
. ,
,  ,
,  .
.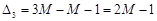 ,
,  ,
,  .
.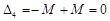 ,
,  ,
,  .
. ,
,  ,
,  .
. записуємо у рядок з номером „3” симплекс-таблиці, а
записуємо у рядок з номером „3” симплекс-таблиці, а  - у рядок з номером „4”. Так як у рядку з оцінками
- у рядок з номером „4”. Так як у рядку з оцінками 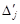 існує одна від’ємна оцінка
існує одна від’ємна оцінка 


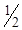


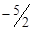
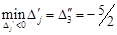 , змінюємо базис і переходимо до нового базисного розв’язку (табл.1.19).
, змінюємо базис і переходимо до нового базисного розв’язку (табл.1.19).




 , тоді переходимо до оцінок
, тоді переходимо до оцінок 



 буде невід’ємною при достатньо великих
буде невід’ємною при достатньо великих  ,
,  . Оскільки всі штучні змінні
. Оскільки всі штучні змінні  ,
,  .
.


