
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модифікований симплекс-методСодержание книги
Поиск на нашем сайте
Розглянемо задачу лінійного програмування, записану у канонічному вигляді:
Нехай Визначимо вектор
тоді
Розрахунки зручніше проводити, якщо записувати їх результати у вигляді таблиць: допоміжної та основної. Допоміжна таблиця (табл.1.22) відрізняється від звичайної симплекс-таблиці тим, що має додаткові рядки та стовпчики, в яких записують значення Основна таблиця (табл.1.23) має декілька відмінностей від звичайної симплекс-таблиці: 1) замість стовпчиків векторів 2) у 3) основна таблиця має один додатковий стовпчик, у перших
Таблиця 1.22.
Таблиця 1.23.
Спочатку визначають вектор Якщо серед чисел В перших Якщо серед чисел Вважаючи Отже, процес розв’язування задачі модифікованим симплекс-методом включає такі етапи: 1. Знаходять опорний план задачі. 2. З компонент векторів початкового базису складають матрицю 3. Знаходять вектор 4. Підраховують числа 5. Обчислюють компоненти вектора 6. За правилами звичайного симплекс-методу знаходять провідний рядок і обчислюють компоненти нового опорного плану і матрицю 7. Перевіряють новий базисний розв’язок на оптимальність, тобто повертаються до п.3. Приклад 1.15. Розв’язати модифікованим симплекс-методом наступну задачу:
Ця задача має базисний розв’язок Складемо допоміжну та основну таблиці (табл.1.24 і табл.1.25). На підставі початкових даних заповнимо перші три рядки стовпчиків векторів Знайдемо компоненти вектора
Запишемо їх в четвертому рядку табл. 1.25, де також заповнимо клітинку стовпчика
Знайдені компоненти вектора
Оскільки серед чисел
Таблиця 1.24.
Таблиця 1.25.
Серед компонент вектора
Таблиця 1.26
Знайдемо компоненти вектора
Запишемо їх в четвертому рядку табл. 1.26 і у відповідному стовпчику табл. 1.24. Підрахуємо числа
Запишемо ці числа в п’ятому рядку табл.1.24. Оскільки серед них є від’ємні, то цей опорний план не оптимальний. В табл.1.26 відводимо останній стовпчик для вектора
Знайдені числа записуємо у стовпчику вектора Таблиця 1.27
Заповнюємо перші три рядки табл. 1.27, обчислюємо компоненти вектора Зауваження. Модифікований симплекс-метод є більш ефективним з точки зору кількості обчислень, ніж симплекс-метод, якщо кількість змінних більше кількості обмежень
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.125 (0.008 с.) |

 ,
,
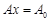 ,
,
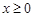 .
.
 — базисний розв’язок цієї задачі, що визначається базисом
— базисний розв’язок цієї задачі, що визначається базисом 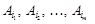 . З компонент цих векторів складемо матрицю
. З компонент цих векторів складемо матрицю 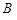 , для якої можна знайти обернену матрицю
, для якої можна знайти обернену матрицю 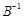 .
.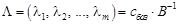 ,
,
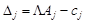 .
.
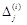 та координати векторів
та координати векторів  , отримані в процесі знаходження розв’язку задачі.
, отримані в процесі знаходження розв’язку задачі.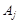 з відповідними коефіцієнтами числової функції
з відповідними коефіцієнтами числової функції 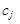 записують стовпчики векторів
записують стовпчики векторів  , координатами яких є відповідні стовпчики матриці
, координатами яких є відповідні стовпчики матриці 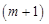 -му рядку записують компоненти векторів
-му рядку записують компоненти векторів 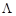 , а не числа
, а не числа 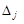 ;
;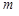 рядках якого записують координати вектора
рядках якого записують координати вектора 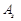 в базисі
в базисі 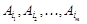 і який слід включити до базису на наступній ітерації.
і який слід включити до базису на наступній ітерації.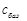
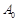
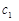

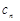
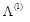
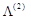

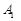
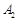
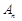
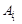
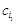


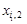
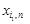

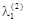
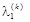
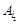
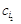
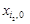
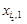
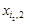

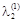
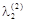

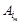
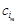

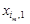


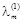

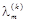
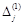

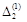
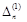
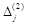

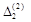
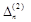

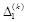

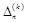

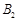



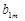
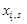

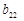

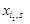
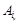

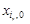



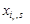
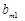
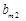
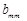
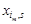

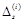
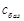 на відповідні вектори
на відповідні вектори 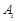 , тобто за формулою (1.7.4). Знайдені компоненти вектора
, тобто за формулою (1.7.4). Знайдені компоненти вектора 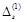 , тоді останній стовпчик таблиці 1.23 відводять для вектора
, тоді останній стовпчик таблиці 1.23 відводять для вектора 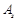 , компоненти якого вказано в табл. 1.22.
, компоненти якого вказано в табл. 1.22. немає додатних, то задача не має розв’язку. Якщо додатні числа є, то знаходять відношення
немає додатних, то задача не має розв’язку. Якщо додатні числа є, то знаходять відношення  і визначають серед них мінімальне. Нехай
і визначають серед них мінімальне. Нехай  . Тоді новий базисний розв’язок визначається базисом, що отримується з вихідного заміною вектора
. Тоді новий базисний розв’язок визначається базисом, що отримується з вихідного заміною вектора  -й рядок і стовпчик вектора
-й рядок і стовпчик вектора  .
. . Якщо всі
. Якщо всі  , то базисний розв’язок є оптимальним розв’язком задачі. Якщо серед
, то базисний розв’язок є оптимальним розв’язком задачі. Якщо серед  .
.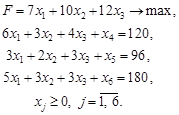
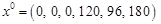 , який визначається базисом, що утворений векторами
, який визначається базисом, що утворений векторами  . Компоненти цих векторів визначають одиничну матрицю
. Компоненти цих векторів визначають одиничну матрицю 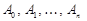 допоміжної таблиці, а також перші три рядки стовпчиків векторів
допоміжної таблиці, а також перші три рядки стовпчиків векторів 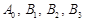 основної таблиці.
основної таблиці.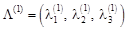 за формулою (1.7.4):
за формулою (1.7.4):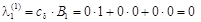

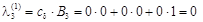
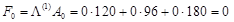
 ,
,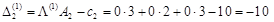 ,
, ,
, .
.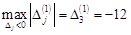 . Тому останній стовпчик табл. 1.24 відводимо для вектора
. Тому останній стовпчик табл. 1.24 відводимо для вектора 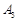 , в якому запишемо компоненти розкладу вектора
, в якому запишемо компоненти розкладу вектора 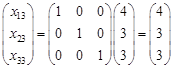 .
.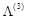
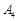


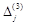

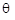
 4
4
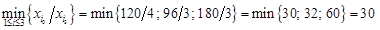 , яке досягається при
, яке досягається при 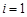 . Вважаючи рядок
. Вважаючи рядок  3/4
3/4
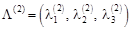 :
: ,
,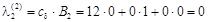 ,
,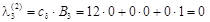 .
.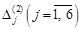 :
: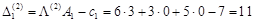 ,
,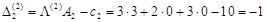 ,
, ,
,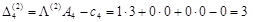 ,
,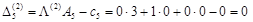 ,
,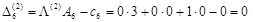 .
.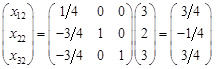 .
. . Оскільки серед них немає від’ємних, то базисний розв’язок
. Оскільки серед них немає від’ємних, то базисний розв’язок  є оптимальним. При цьому цільова функція задачі набуває максимального значення
є оптимальним. При цьому цільова функція задачі набуває максимального значення 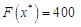 .
.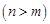 . Це пов’язано з тим, що у модифікованому симплекс-методі в основній таблиці на кожній ітерації розкладаються за базисом тільки
. Це пов’язано з тим, що у модифікованому симплекс-методі в основній таблиці на кожній ітерації розкладаються за базисом тільки  вектора (
вектора ( , а також
, а також 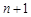 вектор (
вектор (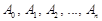 ).
).


