
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття виродженості задач лінійного програмування та спосіб усунення зациклювання у симплекс-методіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В пункті 1.4.1 алгоритм симплекс-методу розглядався у припущенні, що задача невироджена. Нехай тепер дана КЗЛП, для якої Нехай У випадку невиродженої ЗЛП симплекс-метод за скінчену кількість кроків дає можливість одержати оптимальний розв’язок або встановити факт нерозв’язуваності задачі. Це випливає з того, що кожному базисному розв’язку відповідає свій базис. Кількість базисів не перевищує Для вироджених задач лінійного програмування вироджений розв’язок, у якого кількість додатних компонент менше кількості базисних векторів, може бути або початковим, або виникнути у процесі розв’язування задачі. Наприклад, розглянемо задачу
Вектор Поточний базисний розв’язок може стати виродженим у ситуації, коли, користуючись симплекс-методом, неоднозначно визначається вектор, який треба вивести з базису. Тобто мінімальне значення Тоді, вводячи в базис вектор Нехай Припустимо, що для нього існує від’ємна оцінка Переходимо до нового базису, замінюючи вектором Але, якщо хоча б одне з чисел А повний базисний розв’язок
Тобто, нові значення базисних координат співпадають із старими значеннями, і значення цільової функції після цієї ітерації залишається незмінним. Отже, змінився лише базис: замість базису У зв’язку зі зміною складу базисних змінних зміняться оцінки Оскільки число наборів базисних векторів скінчене, то після деякого числа “холостих” ітерацій приходимо до одного з висновків: а) розв’язок оптимальний; б) задача нерозв’язувана; в) отриманий базисний розв’язок був на попередніх ітераціях. Останній висновок означає, що процес обчислення зациклився, тобто після ряду ітерацій ми повертаємося до вже раніше використаного базису. Тому в алгоритмі симплекс-методу передбачена процедура, що усуває зациклювання. Нехай Якщо Якщо Якщо Гарантується, що знайдеться таке Приклад 1.14.
Приведемо задачу до канонічної форми:
Початковим опорним розв’язком є вектор Таблиця 1.21.
На першій ітерації Оптимальним розв’язком буде вектор Розглянемо геометричну інтерпретацію цього прикладу
Рис.1.4.
Через точку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.006 с.) |

 , яка має допустимі розв’язки,
, яка має допустимі розв’язки, 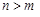 , але умова невиродженості усіх базисних розв’язків не виконана. Задача лінійного програмування, яка має хоча б один вироджений розв’язок, називається виродженою, у протилежному випадку – невиродженою.
, але умова невиродженості усіх базисних розв’язків не виконана. Задача лінійного програмування, яка має хоча б один вироджений розв’язок, називається виродженою, у протилежному випадку – невиродженою. - будь-який базисний розв’язок,
- будь-який базисний розв’язок, 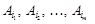 - його базис. Розглянемо спочатку випадок невиродженої ЗЛП.
- його базис. Розглянемо спочатку випадок невиродженої ЗЛП. , де
, де 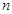 - кількість змінних задачі,
- кількість змінних задачі,  - ранг матриці
- ранг матриці 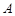 . Отже кількість базисних розв’язків також скінченна. У невиродженому випадку значення цільової функції ЗЛП зростає на кожному кроці. Тобто гарантується неможливість повернення до попередніх планів. Таким чином для невиродженої ЗЛП за скінченну кількість кроків прийдемо до результату.
. Отже кількість базисних розв’язків також скінченна. У невиродженому випадку значення цільової функції ЗЛП зростає на кожному кроці. Тобто гарантується неможливість повернення до попередніх планів. Таким чином для невиродженої ЗЛП за скінченну кількість кроків прийдемо до результату. ,
, ,
, ,
, ,
,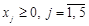 .
. є виродженим початковим базисним планом, якому відповідає як базис з векторів
є виродженим початковим базисним планом, якому відповідає як базис з векторів  та
та  , так і базис, що складається з векторів
, так і базис, що складається з векторів  та
та  виходить для декількох значень
виходить для декількох значень  (
( - номер вектора, який вводиться до базису,
- номер вектора, який вводиться до базису,  ).
).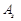 замість вектора
замість вектора 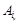 , де
, де  — один з номерів, для яких досягається мінімум
— один з номерів, для яких досягається мінімум  , ми прийдемо до виродженого розв’язку.
, ми прийдемо до виродженого розв’язку.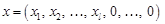 , де
, де 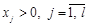 — початковий, або поточний вироджений базисний, розв’язок,
— початковий, або поточний вироджений базисний, розв’язок, 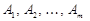 — його базис
— його базис  .
.  .
. , для якої є додатні
, для якої є додатні 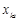 .
. для якого
для якого  .
. додатне, тоді
додатне, тоді  .
. ,
,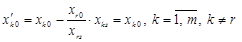 .
. маємо базис
маємо базис 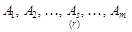 .
.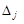 , і процес обчислення може бути продовжений, хоча на кожній ітерації значення цільової функції буде залишатись незмінним.
, і процес обчислення може бути продовжений, хоча на кожній ітерації значення цільової функції буде залишатись незмінним.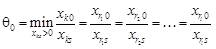 .
.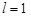 , то вектор
, то вектор  виводиться з базису.
виводиться з базису. , то обчислюємо відношення
, то обчислюємо відношення  і знаходим
і знаходим  . Якщо
. Якщо  досягається для одного номера, наприклад
досягається для одного номера, наприклад  , то вектор
, то вектор  виводиться з базису.
виводиться з базису. і знаходимо мінімальне з них
і знаходимо мінімальне з них 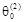 . Якщо
. Якщо  , для якого
, для якого  досягається лише для одного номера
досягається лише для одного номера 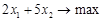 ,
, ,
, ,
,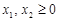 .
. .
. ,
, .
. з базисом
з базисом  . Розв’язування задачі наведено у таблиці 1.21.
. Розв’язування задачі наведено у таблиці 1.21.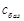

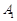
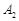

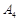
 . Виникла неоднозначна ситуація з вибором вектора, який треба вивести з базису. Тоді вибір такого вектора можна зробити довільно – або
. Виникла неоднозначна ситуація з вибором вектора, який треба вивести з базису. Тоді вибір такого вектора можна зробити довільно – або  , залишаючись базисною, набуває нульове значення. А тому цей опорний план
, залишаючись базисною, набуває нульове значення. А тому цей опорний план  є виродженим. Критерій оптимальності для нього не виконується. Відповідно на наступній ітерації
є виродженим. Критерій оптимальності для нього не виконується. Відповідно на наступній ітерації  , а це означає, що попереднє значення цільової функції не зміниться,
, а це означає, що попереднє значення цільової функції не зміниться,  .
. .
.


 проходять три прямі, які її обумовлюють. В задачі всього дві змінні, тому цю точку називають перевизначеною, так як для її ідентифікації достатньо тільки двох прямих. Звідси випливає висновок, що одне з обмежень задачі є несуттєвим (
проходять три прямі, які її обумовлюють. В задачі всього дві змінні, тому цю точку називають перевизначеною, так як для її ідентифікації достатньо тільки двох прямих. Звідси випливає висновок, що одне з обмежень задачі є несуттєвим (


