
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математична модель задачі 10.4Содержание книги
Поиск на нашем сайте
Позначимо
Канонічна форма задачі Домножуємо нерівності (15) і цільову функцію (17) на (-1)
Введемо нові невід’ємні змінні
Складаємо симплекс – таблицю 1. с имплекс - таблиця 1
Вибір розв’язуючого елемента 1. Розв’язуючий елемент повинен бути від’ємним! 2. Розв’язуючий рядок – P7 знаходимо з умови min (P0). min (-100;-100;-300) = -300. 3. Розв’язуючий стовпець – P4 знаходимо з умови min (|Dj/aij|), тут i – номер розв’язуючого рядка. min (200/25; 50/80; 70/120; 100/500) = 100/500. 4. Вектор P7 виходить з базису, Вектор P4 входить у базис. 5. Розв’язуючий елемент – число -500 – знаходиться на перетині розв’язуючого рядка P7 і розв’язуючого стовпця P4. Алгоритм двоїстого симплекс-методу 1. Розв’язуючий рядок P7 ділимо на розв’язуючий елемент – число -500; 2. Базисні стовпці P5, P6 i P7 повинні бути одиничними векторами; 3. Усі інші елементи таблиці (стовпці P0 - P4 крім рядка P7) перераховуються згідно правила прямокутника:
Тут В результаті отримуємо наступну симплекс-таблицю 2. симплекс - таблиця 2
План, який представлений у цій таблиці не є оптимальним, оскільки серед вільних членів P0 є від’ємні. За описаним вище алгоритмом знаходимо розв’язуючий рядок – P6 та розв’язуючи стовпець – P1. Змінна P6 виходить з базису, змінна P1 входить у базис. Застосовуючи алгоритм двоїстого симплекс-методу отримуємо наступну симплекс-таблицю 3. симплекс - таблиця 3
5. Оскільки всі P0 ³ 0, отримано оптимальний розв’язок задачі. Оптимальні значення параметрів x1, x4 i x5 знаходимо у стовпчику P0. Невідомі x2, x3, x6 i x7 яких немає у базисі є вільними і дорівнюють нулю. Відповідь. Оптимальний харчовий раціон має вигляд: x1 = 0.63; x2 = 0; x3 = 0; x4 = 0.57; x5 = 39.8; x6 = 0; x7 = 0. Fmin (сумарна вартість) = 182,61. Таблиця 4. В а р і а н т и з а в д а н ь д о т е м и 1 0
Тема 11 Задача лінійного програмування: задача про розріз труб 11.1. Завдання. Побудувати математичну модель задачі лінійного програмування (задача на мінімум відходів). Звести задачу до канонічної форми. Розв’язати задачу двоїстим симплекс-методом. 11.2. Постановка задачі: В обробку поступила партія труб довжиною L = 7.5 м кожна. Необхідно розрізати труби, отримавши N1= 50 заготовок довжиною L1 = 3.5 м, N2= 30 заготовок довжиною L2 = 2.5 м і N3= 40 заготовок довжиною L3 = 2.0 м. Побудувати оптимальний план розрізу при якому сумарна довжина відходів буде мінімальною. Таблиця 5. Таблиця варіантів розрізу
Математична модель задачі Позначимо x і – кількість труб, розрізаних згідно і – го варіанту. Тоді отримаємо математичну модель задачі у наступному вигляді:
Канонічна форма задачі Домножимо нерівності (19) і цільову функцію (21) на (-1). Введемо нові невід’ємні змінні
Таблиця 6. В а р і а н т и з а в д а н ь д о т е м и 1 1
Тема12 Транспортна задача Постановка задачі. Три бригади за тиждень виробляють корми в кількостях a1, a2 i a3 відповідно. Їх необхідно розвезти на 5 ферм, згідно з поданими заявками, у кількостях b1, b2, b3, b4, b5. Вартість перевезення вважається пропорційною до кількості завантаженого корму xij і відстані від постачальника (бригади) до споживача (ферми) cij. Необхідно скласти такий план перевезень кормів, загальна вартість якого буде мінімальною. Необхідні для розрахунку параметри представлені у наступній Таблиці 7. Таблиця 7. Технологічні параметри транспортної задачі.
Необхідно скласти оптимальний план закріплення бригад за фермами з умовою мінімальної вартості перевезення кормів.
12.2. Математична модель транспортної задачі Позначимо xij – кількість одиниць корму, який планується перевезти від i – го постачальника (сівозміни) до j – го споживача (ферми). Оскільки всі вантажі повинні бути вивезені, то мають місце такі рівності:
Оскільки всі потреби споживачів повинні бути задоволені, то мають місце такі рівності:
Оскільки вантажі перевозяться лише в одну сторону, очевидно, що:
Загальна вартість перевезення вважається пропорційною до кількості перевезених вантажів та відстані від постачальника до споживача і повинна бути мінімальною:
Якщо виконується умова
12.3. Алгоритм розв’язування ТЗ Потрібно: 1. скласти початковий опорний план задачі методом північно-західного кута; 2. скласти початковий опорний план задачі методом мінімального тарифа; 3. вибравши кращий з побудованих початкових планів, виконати його оптимізацію методом потенціалів за такою схемою: 3.1. скласти систему рівнянь (по базисних клітинах) для визначення потенціалів рядків Ui та стовпців Vj та, прийнявши U1=0, розв’язати отриману систему; 3.1.1. визначити характеристики вільних клітин за формулою
3.2. якщо всі характеристики є невід’ємні, завершити розв’язування задачі. Виписати оптимальний план перевезень у вигляді матриці, а також мінімальне значення вартості перевезень Fmin; 3.3. якщо не всі характеристики є невід’ємні, необхідно вибрати найбільшу додатну характеристику і побудувати для відповідної вільної клітини таблиці цикл. Позначити вершини циклу умовними знаками “+” (збільшити вантажо-потік) i “-” (зменшити вантажопотік). Початкова вільна вершина позначається знаком “+”, а всі інші – по черзі “-” i “+”; серед всіх вершин, позначених знаком “-”, вибрати найменше перевезення – m. Для всіх вершин, позначених знаком “+”збільшити перевезення на m, для вершин, позначених знаком “-” зменшити перевезення на m. Перейти до пункту 3.1
12.4. Побудова початкового опорного плану ТЗ Таблиця 8. Метод північно – західного кута
F = 60*4 + 70*3 + 10*2 + 110*8 + 70*4 + 60*7 + 100*2 = 240 + 210 + 20 + 880 + 280 + 420 + 200 = 2250 – вартість перевезень
Таблиця 9. Метод мінімального тарифа
F = 10*2 + 130*2 + 60*1 + 20*4 + 100*1 + 50*7 + 110*3 = 20 + 260 + 60 + 80 + 100 + 350 + 330 = 1200 – вартість перевезень
12.5. Метод потенціалів За основу виберемо план, складений по методу мінімального тарифа. Оптимізуємо даний план за методом потенціалів. Для кожного i – го рядка та j – го стовпця введемо певну їх ознаку – потенціал. Складаємо систему рівнянь (по базисних клітинках плану) для визначення потенціалів рядків і стовпців, використовуючи наступну формулу U1 + V3 = 2; U1 + V4 = 2; U2 + V1 = 1; U2 + V2 = 4; U2 + V5 = 1; U3 + V2 = 7; U3 + V3 = 3. Приймемо U1 = 0. Тоді отримаємо наступний розв’язок системи: U1 =0; V3 = 2; U1 =0; V4 = 2; U2 =-2; V1 = 3; U2 =-2; V2 = 6; U2 =-2; V5 = 3; U3 =1; V2 = 6; U3 =1; V3 = 2. Для кожної вільної клітинки введемо поняття її характеристики
Тут D11 = u1 + v1 – c11 = 0 + 3 – 4 = -1; D12 = u1 + v2 – c12 = 0 + 6 – 3 = +3; D15 = u1 + v5 – c15 = 0 + 3 – 4 = -1; D23 = u2 + v3 – c23 = -2 + 2 – 8 = -8; D24 = u2 + v4 – c24 = -2 + 2 – 4 = -4; D31 = u3 + v1 – c31 = 1 + 3 – 9 = -5; D34 = u3 + v4 – c34 = 1 + 2 – 7 = -4; D35 = u3 + v5 – c35 = 1 + 3 – 2 = +2. Характеристики D12 і D35 є додатніми. Це свідчить про неоптимальність плану. Клітинку A1B2 необхідно включити в план. Деяку клітинку необхідно виключити з базису. Для цього складаємо цикл вільної клітини. Клітина A1B2 буде початком циклу.
12.6. Перерозподіл вантажопотоків по вершинах циклу - 1
Будуємо цикл. Це є ламана лінія, вершини якої розташовані у клітинах таблиці, а ланки – вздовж рядків, чи стовпців. В кожній вершині циклу зустрічається дві ланки, одна з яких знаходиться у рядку, а друга у стовпці. Початковою вершиною завжди виступає вільна клітина. Всі інші вершини – це базисні клітини. Форма циклу – це прямокутник, “чобіт”, або ”вісімка”. Якщо ламана лінія, що утворює цикл перетинається, то точки самоперетину не є вершинами. Початкову клітину циклу A1B2 помічаємо знак “+”. Всі інші кутові вершини циклу по черзі помічаємо знаками “-” i ”+”. В якості перерозподілюваного елемента вибираємо число 10 (мінімальний вантаж серед усіх клітин помічених знаком “-”). До клітинок помічених знаком “+” додаємо число 10, від клітин помічених знаком “-” віднімаємо число 10. Клітина A1B2 входить у базис, клітина A1B3 виходить з базису. Отримуємо новий план Види циклів.
прямокутник “чобіт” ”вісімка”
12.7. Метод потенціалів. Другий крок
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.74 (0.009 с.) |

 – кількість корму P1,
– кількість корму P1,  – кількість корму P2,
– кількість корму P2, 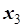 – кількість корму P3,
– кількість корму P3, 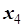 – кількість корму P4. Тоді отримаємо математичну модель задачі:
– кількість корму P4. Тоді отримаємо математичну модель задачі: (15)
(15) (16)
(16) (17)
(17)
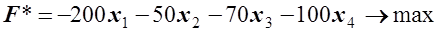
 , і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 7 невідомих).
, і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 7 невідомих).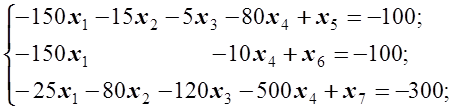
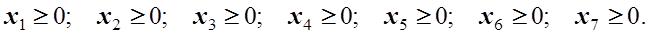

 -оцінка невідомого
-оцінка невідомого  .
. . (18)
. (18)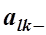 розв’язуючий елемент;
розв’язуючий елемент;  елемент, який перераховується.
елемент, який перераховується. (19)
(19) (20)
(20) . (21)
. (21) і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 10 невідомих).
і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 10 невідомих).

 Задача розв’язується двоїстим симплекс – методом.
Задача розв’язується двоїстим симплекс – методом. (22)
(22) (23)
(23) (24)
(24) (25)
(25) , задача називається закритою.
, задача називається закритою.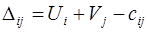 ; (26)
; (26) .
. , яку будемо обчислювати за формулою:
, яку будемо обчислювати за формулою: . (27)
. (27) та
та  - потенціали відповідних рядка і стовпця,
- потенціали відповідних рядка і стовпця,  - тариф даного перевезення. Додатна характеристика вільної клітини свідчить про неоптимальність плану і є підставою для включення даної клітини в новий план. Обчислимо характеристики вільних клітин:
- тариф даного перевезення. Додатна характеристика вільної клітини свідчить про неоптимальність плану і є підставою для включення даної клітини в новий план. Обчислимо характеристики вільних клітин:



 A1
A1


 A3
A3






