
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математична модель задачі у загальному виглядіСодержание книги
Поиск на нашем сайте
Тут x 1 i x 2 – площа, відведена під першу і другу культуру відповідно; c1 i c2 – прибуток з 1 гектара культури відповідно першого і другого типу; aij – затрати ресурсів і -го типу на 1 гектар культури j - го типу; bi – кількість виділених ресурсів для і - ої культури. Приклад Таблиця 1. Технологічна матриця (затрати ресурсів на 1 га площі)
Математична модель задачі 9.4 Позначимо x 1 – площа під культурою 1, x 2 – площа під культурою 2. Тоді отримаємо:
Геометричний спосіб розв’язування Побудуємо симплекс. Для побудови прямої лінії необхідно мати дві опорних точки. Будемо шукати ці точки на осях. При цьому отримаємо такі результати: А лінія 2-а лінія 3-я лінія
Знайдемо координати вершин симплекса. Координати вершин O, A, D вже відомі і становлять: O(0;0), A(0;4), D(6;0). Для знаходження координат вершини B необхідно розв’язати систему двох лінійних рівнянь, які відповідають першій і третій лінії:
В результаті отримаємо B(3.46; 2.62). Для знаходження координат вершини С необхідно розв’язати систему двох лінійних рівнянь, які відповідають другій і третій лінії:
В результаті отримаємо С(5.40; 1.00). Обчислимо значення цільової функції у вершинах симплекса, використовуючи формулу Отримаємо F(O)=0.00; F(A)=4; F(B)=9.54; F(C)=11.8; F(D)=12.00. Отже оптимальний розв’язок відповідає вершині D симплекса і має вигляд:
Табличний симплекс-метод Канонічна форма задачі Введемо нові невід’ємні змінні
Складаємо симплекс – таблицю 1 симплекс-таблиця 1
Тут
Вибір розв’язуючого елемента 1. Розв’язуючий елемент повинен бути додатнім! 2. Розв’язуючий стовпець P1 знаходимо з умови min 3. Розв’язуючий рядок – P4 знаходимо з умови min (P0/aij), тут i – номер розв’язуючого рядка. min (20/2; 30/5; 33/5) = 30/5. 4. Вектор P4 виходить з базису, Вектор P1 входить у базис. 5. Розв’язуючий елемент – число 5 – знаходиться на перетині розв’язуючого рядка P4 і розв’язуючого стовпця P1. Алгоритм звичайного симплекс-методу 1. Розв’язуючий рядок P4 ділимо на розв’язуючий елемент – число 5; 2. Базисні стовпці P1, P3 i P5 повинні бути одиничними векторами; 3. Усі інші елементи таблиці (стовпці P0, P2, P4 крім рядка P4) перераховуються згідно правила прямокутника:
Тут симплекс-таблиця 2
4. Оскільки всі Відповідь. Оптимальний розподіл земельних ресурсів має вигляд: x1 (площа під першу культуру) = 6 га; x2 (площа під другу культуру) = 0 га; x3 = 8; x4 = 0; x5 = 3; Fmax (прибуток) = 12 тис. грн.
Таблиця 2. В а р і а н т и з а в д а н ь д о т е м и 9
Тема 10 Задача лінійного програмування: двоїстий симплекс-метод 10.1. Завдання. Побудувати математичну модель задачі лінійного програмування (задача на мінімум). Звести задачу до канонічної форми. Розв’язати задачу двоїстим симплекс-методом. 10.2. Постановка задачі: Для відгодівлі тварин фермер використовує чотири види корму P1, P2, P3, P4, кожен з яких містить поживні речовини B1, B2, B3. Добова потреба тварини у поживних речовинах дорівнює b1, b2 i b3 відповідно. Ціна корму становить відповідно c1, c2, c3, c4. Вміст поживних речовин у одиниці маси кожного корму відомий і становить a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34 (тут перший індекс позначає номер поживної речовини, а другий – номер корму). Необхідно побудувати харчовий раціон (вказати щоденну кількість кожного корму), вартість якого мінімальна.
Математична модель задачі (для загального випадку)
Тут xj – кількість корму j - го типу; cj – ціна корму j - го типу; aij – вміст поживної речовини i – го типу у одиниці маси корму j -ого типу; bi – добова потреба у i –ій поживній речовині. Приклад. Технологічна матриця задачі про оптимальний харчовий раціон Таблиця 3. Технологічна матриця
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.126.199 (0.008 с.) |

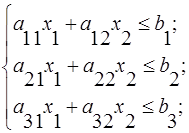 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6)

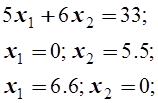


 .
.

 . Отримаємо систему недоозначених рівнянь (3 рівняння, 5 невідомих).
. Отримаємо систему недоозначених рівнянь (3 рівняння, 5 невідомих).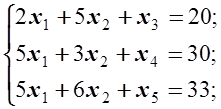 (7)
(7) (8)
(8) (9)
(9) - оцінка невідомого
- оцінка невідомого 
 (10)
(10) . min (-2;-1)=-2.
. min (-2;-1)=-2. . (11)
. (11) розв’язуючий елемент;
розв’язуючий елемент;  елемент, який перераховується.
елемент, який перераховується. ³ 0, отримано оптимальний розв’язок задачі. Оптимальні значення параметрів x3, x1 i x5 знаходимо у стовпчику P0. Невідомі x2 i x4 яких немає у базисі є вільними і дорівнюють нулю. Якби серед оцінок були б від’ємні, довелось би будувати ще одну симплекс таблицю
³ 0, отримано оптимальний розв’язок задачі. Оптимальні значення параметрів x3, x1 i x5 знаходимо у стовпчику P0. Невідомі x2 i x4 яких немає у базисі є вільними і дорівнюють нулю. Якби серед оцінок були б від’ємні, довелось би будувати ще одну симплекс таблицю (12)
(12) (13)
(13)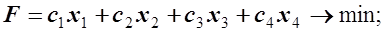 (14)
(14)


