
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Національний університет водного господарства та природокористуванняСодержание книги
Поиск на нашем сайте
Національний університет водного господарства та природокористування Кафедра прикладної математики 100 – 62 МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ Для виконання контрольних та лабораторних робіт з дисципліни “МАТЕМАТИЧНІ МЕТОДИ І МОДЕЛІ” студентами спеціальностей “Землевпорядкування та кадастр” і “Геоінформаційні системи”
Рівне - 2004
Методичні вказівки і завдання для виконання контрольних та лабораторних робіт з дисципліни “Математичні методи і моделі” для студентів всіх форм навчання спеціальностей “Землевпорядкування та кадастр” і “Геоінформаційні системи” / П.М.Грицюк - Рівне, НУВГП, 2004. - 26 с. Укладач: П.М.Грицюк, доцент кафедри прикладної математики Відповідальний за випуск: А.П.Власюк, доктор технічних наук, завідувач кафедри прикладної математики
З М І С Т 1. Вступ……………………………………………………..........…………… 3 2. Тема 9. Задача лінійного програмування............................................... 4 3. Тема 10. Задача лінійного програмування: двоїстий симплекс - метод.……........................................................................................………. 10 Тема 11. Задача лінійного програмування: задача про розріз труб 16 5. Тема 12. Транспортна задача………………………….......................... 19
Вступ Дисципліна “Математичні методи і моделі” є однією з основних дисциплін, необхідних для формування навичок комп’ютерного моделювання у майбутніх інженерів-землевпорядників. Програма дисципліни формувалася з врахуванням важливості тих, чи інших математичних методів і моделей для геоінформатики. Цьому принципу відповідають і дані методичні вказівки. Основна увага в даних методичних вказівках приділена методам моделювання складних географічних систем, а також математичним методам дослідження отриманих моделей. У методвказівках розглянуто чотири задачі, які утворюють другу частину циклу лабораторних робіт. Для кожного завдання здійснюється постановка задачі, наводиться коротка теоретична довідка або ж математична модель задачі, вказується метод розв’язування та основні розрахункові формули, наводиться рекомендований вигляд розрахункових таблиць. Всі задачі відносяться до розділу “Математичне програмування” і є характерними для математичного забезпечення ГІС. Розв’язування цих задач покликано поглибити розуміння деяких сторін математичного забезпечення геоінформатики. В якості ілюстрацій наводяться плани та схеми, які унаочнюють розв’язування задач. Для кожної з задач наводиться таблиця вихідних даних. Завдяки цьому методвказівки можуть використовуватися для виконання лабораторних, контрольних і самостійних робіт. За результатами вивчення курсу “Математичні методи і моделі” студент – заочник повинен виконати контрольну роботу. Розглянуті нижче задачі можуть бути використані в якості завдань для неї. Дані для кожного завдання визначаються номером варіанта. Номер варіанта визначається двома останніми цифрами залікової книжки NN за формулами:
У контрольній роботі потрібно навести: умову кожної задачі (загальна умова + дані для свого варіанту), детальний розв’язок у табличній формі з необхідними поясненнями і графічними ілюстраціями. Студент допускається до іспиту лише при наявності позитивної рецензії на контрольну роботу і відмітки про допуск до співбесіди.
Тема 9 Задача лінійного програмування 9.1. Завдання. Побудувати математичну модель задачі лінійного програмування. Розв’язати задачу графічним методом. Звести задачу до канонічної форми. Розв’язати задачу табличним симплекс-методом. Дати економічну інтерпретацію розв’язку задачі. 9.2. Постановка задачі про оптимальний розподіл земельних ресурсів: Сільськогосподарське підприємство вирощує дві культури P1 і P2, використовуючи три типи ресурсів (робоча сила, фінансові ресурси, рухомий склад), запаси яких дорівнюють b1, b2 i b3 відповідно. Прибуток з 1 гектара культури становить відповідно c1 і c2. Затрати ресурсів (на 1 гектар) на виробництво культур відомі і дорівнюють a11, a12, a21, a22, a31, a32. Необхідно знайти такий план розподілу площ під культури, який забезпечує максимальний прибуток від її реалізації.
Приклад Таблиця 1. Технологічна матриця (затрати ресурсів на 1 га площі)
Геометричний спосіб розв’язування Побудуємо симплекс. Для побудови прямої лінії необхідно мати дві опорних точки. Будемо шукати ці точки на осях. При цьому отримаємо такі результати: А лінія 2-а лінія 3-я лінія
Знайдемо координати вершин симплекса. Координати вершин O, A, D вже відомі і становлять: O(0;0), A(0;4), D(6;0). Для знаходження координат вершини B необхідно розв’язати систему двох лінійних рівнянь, які відповідають першій і третій лінії:
В результаті отримаємо B(3.46; 2.62). Для знаходження координат вершини С необхідно розв’язати систему двох лінійних рівнянь, які відповідають другій і третій лінії:
В результаті отримаємо С(5.40; 1.00). Обчислимо значення цільової функції у вершинах симплекса, використовуючи формулу Отримаємо F(O)=0.00; F(A)=4; F(B)=9.54; F(C)=11.8; F(D)=12.00. Отже оптимальний розв’язок відповідає вершині D симплекса і має вигляд:
Табличний симплекс-метод Канонічна форма задачі Введемо нові невід’ємні змінні
Складаємо симплекс – таблицю 1 симплекс-таблиця 1
Тут
Таблиця 2. В а р і а н т и з а в д а н ь д о т е м и 9
Тема 10 Задача лінійного програмування: двоїстий симплекс-метод 10.1. Завдання. Побудувати математичну модель задачі лінійного програмування (задача на мінімум). Звести задачу до канонічної форми. Розв’язати задачу двоїстим симплекс-методом. 10.2. Постановка задачі: Для відгодівлі тварин фермер використовує чотири види корму P1, P2, P3, P4, кожен з яких містить поживні речовини B1, B2, B3. Добова потреба тварини у поживних речовинах дорівнює b1, b2 i b3 відповідно. Ціна корму становить відповідно c1, c2, c3, c4. Вміст поживних речовин у одиниці маси кожного корму відомий і становить a11, a12, a13, a14, a21, a22, a23, a24, a31, a32, a33, a34 (тут перший індекс позначає номер поживної речовини, а другий – номер корму). Необхідно побудувати харчовий раціон (вказати щоденну кількість кожного корму), вартість якого мінімальна.
Таблиця 3. Технологічна матриця
Канонічна форма задачі Домножуємо нерівності (15) і цільову функцію (17) на (-1)
Введемо нові невід’ємні змінні
Таблиця 4. В а р і а н т и з а в д а н ь д о т е м и 1 0
Тема 11 Задача лінійного програмування: задача про розріз труб 11.1. Завдання. Побудувати математичну модель задачі лінійного програмування (задача на мінімум відходів). Звести задачу до канонічної форми. Розв’язати задачу двоїстим симплекс-методом. 11.2. Постановка задачі: В обробку поступила партія труб довжиною L = 7.5 м кожна. Необхідно розрізати труби, отримавши N1= 50 заготовок довжиною L1 = 3.5 м, N2= 30 заготовок довжиною L2 = 2.5 м і N3= 40 заготовок довжиною L3 = 2.0 м. Побудувати оптимальний план розрізу при якому сумарна довжина відходів буде мінімальною. Таблиця 5. Таблиця варіантів розрізу
Математична модель задачі Позначимо x і – кількість труб, розрізаних згідно і – го варіанту. Тоді отримаємо математичну модель задачі у наступному вигляді:
Канонічна форма задачі Домножимо нерівності (19) і цільову функцію (21) на (-1). Введемо нові невід’ємні змінні
Таблиця 6. В а р і а н т и з а в д а н ь д о т е м и 1 1
Тема12 Транспортна задача Постановка задачі. Три бригади за тиждень виробляють корми в кількостях a1, a2 i a3 відповідно. Їх необхідно розвезти на 5 ферм, згідно з поданими заявками, у кількостях b1, b2, b3, b4, b5. Вартість перевезення вважається пропорційною до кількості завантаженого корму xij і відстані від постачальника (бригади) до споживача (ферми) cij. Необхідно скласти такий план перевезень кормів, загальна вартість якого буде мінімальною. Необхідні для розрахунку параметри представлені у наступній Таблиці 7. Таблиця 7. Технологічні параметри транспортної задачі.
Необхідно скласти оптимальний план закріплення бригад за фермами з умовою мінімальної вартості перевезення кормів.
12.2. Математична модель транспортної задачі Позначимо xij – кількість одиниць корму, який планується перевезти від i – го постачальника (сівозміни) до j – го споживача (ферми). Оскільки всі вантажі повинні бути вивезені, то мають місце такі рівності:
Оскільки всі потреби споживачів повинні бути задоволені, то мають місце такі рівності:
Оскільки вантажі перевозяться лише в одну сторону, очевидно, що:
Загальна вартість перевезення вважається пропорційною до кількості перевезених вантажів та відстані від постачальника до споживача і повинна бути мінімальною:
Якщо виконується умова
12.3. Алгоритм розв’язування ТЗ Потрібно: 1. скласти початковий опорний план задачі методом північно-західного кута; 2. скласти початковий опорний план задачі методом мінімального тарифа; 3. вибравши кращий з побудованих початкових планів, виконати його оптимізацію методом потенціалів за такою схемою: 3.1. скласти систему рівнянь (по базисних клітинах) для визначення потенціалів рядків Ui та стовпців Vj та, прийнявши U1=0, розв’язати отриману систему; 3.1.1. визначити характеристики вільних клітин за формулою
3.2. якщо всі характеристики є невід’ємні, завершити розв’язування задачі. Виписати оптимальний план перевезень у вигляді матриці, а також мінімальне значення вартості перевезень Fmin; 3.3. якщо не всі характеристики є невід’ємні, необхідно вибрати найбільшу додатну характеристику і побудувати для відповідної вільної клітини таблиці цикл. Позначити вершини циклу умовними знаками “+” (збільшити вантажо-потік) i “-” (зменшити вантажопотік). Початкова вільна вершина позначається знаком “+”, а всі інші – по черзі “-” i “+”; серед всіх вершин, позначених знаком “-”, вибрати найменше перевезення – m. Для всіх вершин, позначених знаком “+”збільшити перевезення на m, для вершин, позначених знаком “-” зменшити перевезення на m. Перейти до пункту 3.1
12.4. Побудова початкового опорного плану ТЗ Таблиця 8. Метод північно – західного кута
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.3.17 (0.01 с.) |




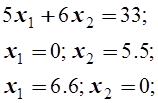


 .
.

 . Отримаємо систему недоозначених рівнянь (3 рівняння, 5 невідомих).
. Отримаємо систему недоозначених рівнянь (3 рівняння, 5 невідомих).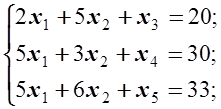 (7)
(7) (8)
(8) (9)
(9) - оцінка невідомого
- оцінка невідомого 
 (10)
(10)
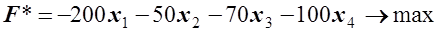
 , і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 7 невідомих).
, і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 7 невідомих).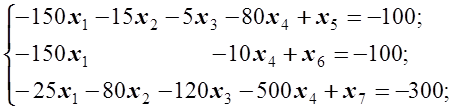
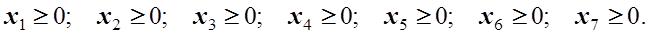

 (19)
(19) (20)
(20) . (21)
. (21) і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 10 невідомих).
і додамо їх до лівих частин нерівностей. Отримаємо систему недоозначених рівнянь (3 рівняння, 10 невідомих).

 Задача розв’язується двоїстим симплекс – методом.
Задача розв’язується двоїстим симплекс – методом. (22)
(22) (23)
(23) (24)
(24) (25)
(25) , задача називається закритою.
, задача називається закритою.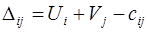 ; (26)
; (26)


