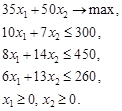Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна задача лінійного програмуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Загальну задачу лінійного програмування (ЗЛП) визначимо таким чином: необхідно знайти такі значення
і які задовольняють системі лінійних обмежень
де символ Співвідношення (1.1.2) називаються обмеженнями задачі лінійного програмування, а функція (1.1.1) — цільовою функцією задачі лінійного програмування. Сукупність точок
Будь-яка точка Допустимий розв’язок Тобто, для будь-якого іншого допустимого розв’язку
якщо задача на максимум, і
якщо задача на мінімум. Оптимальний розв’язок будемо записувати таким чином:
Приклад 1.1. Знайти
У цій задачі Значення цільової функції відповідно дорівнюють Зауважимо, що не для кожної задачі лінійного програмування існує оптимальний розв’язок, навіть якщо існують допустимі розв’язки. Крім того, не кожна ЗЛП має допустимі розв’язки, оскільки система обмежень (рівностей та нерівностей) (1.1.2) може бути несумісною. Задачу лінійного програмування, яка має допустимі розв’язки (тобто система (1.1.2) сумісна), надалі будемо називати допустимою; задачу з несумісною системою обмежень — недопустимою. У більшості економічних задач зміст змінних Такі обмеження будемо називати прямими обмеженнями на змінні. Методи розв’язування ЗЛП охоплюють велику кількість різноманітних конкретних варіантів, які відрізняються між собою як вимогами до цільових функцій (знайти максимум чи мінімум), так і структурою системи обмежень (самі лише нерівності або рівності чи поєднання рівностей і нерівностей). Один з варіантів ЗЛП узято за стандарт — канонічна форма задачі лінійного програмування (КЗЛП). КЗЛП визначається таким чином: знайти вектор
(будемо це записувати так: і задовольняє системі обмежень
Позначимо
Тоді КЗЛП можна записати у матричній формі:
або у векторній формі
ЗЛП, записану у вигляді
будемо називати ЗЛП у стандартній формі, а задачу виду:
- ЗЛП у симетричній формі. Всі форми ЗЛП є еквівалентними з точки зору розв’язку задачі. Неважко бачити, що будь-яку ЗЛП можна привести до канонічного виду. Задача мінімізації Обмеження-нерівності
перетворюються у обмеження-рівності за допомогою невід’ємних додаткових змінних:
Нарешті, якщо знак деяких змінних
Приклад 1.2. Привести ЗЛП до канонічного виду.
Оскільки знак змінної Отже КЗЛП має вигляд:
Наведемо приклад запису лінійної математичної моделі задачі про оптимальне використання сировини. Приклад 1.3. Із сировини трьох видів — Необхідно визначити такі обсяги виробництва кожного з видів продукції Вихідні дані задачі наведено в табл.1.1. Таблиця 1.1.
Математична модель цієї задачі має такий вигляд
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.179.96 (0.006 с.) |

 змінних
змінних  , при яких досягається максимум (мінімум) функції
, при яких досягається максимум (мінімум) функції

 заміняє один із знаків ≤, =, ≥;
заміняє один із знаків ≤, =, ≥;  - задані дійсні числа.
- задані дійсні числа. , які задовольняють обмеженням (1.1.2), називається допустимою множиною (областю) ЗЛП, котру ми будемо записувати також у вигляді
, які задовольняють обмеженням (1.1.2), називається допустимою множиною (областю) ЗЛП, котру ми будемо записувати також у вигляді .
.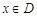 називається допустимим розв’язком або планом задачі.
називається допустимим розв’язком або планом задачі.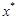 , що доставляє максимум (мінімум) цільової функції називається оптимальним розв’язком або оптимальним планом, або просто розв’язком ЗЛП.
, що доставляє максимум (мінімум) цільової функції називається оптимальним розв’язком або оптимальним планом, або просто розв’язком ЗЛП.
 ,
, ,
,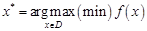 . При цьому
. При цьому  будемо називати оптимальним значенням цільової функції або оптимумом ЗЛП.
будемо називати оптимальним значенням цільової функції або оптимумом ЗЛП.

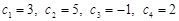 . У перших трьох обмеженнях задачі (1.1.3)
. У перших трьох обмеженнях задачі (1.1.3)  ”. Наприклад, вектори
”. Наприклад, вектори  є допустимими планами, а вектор
є допустимими планами, а вектор  — не допустимий, тому що він задовольняє лише першим трьом рівнянням, а четверте обмеження не виконується
— не допустимий, тому що він задовольняє лише першим трьом рівнянням, а четверте обмеження не виконується 
 та
та  . Оскільки,
. Оскільки, 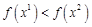 , тоді допустимий розв’язок
, тоді допустимий розв’язок 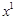 не є оптимальним. Щодо розв’язку
не є оптимальним. Щодо розв’язку  , то без додаткових досліджень не можна визначити, чи буде він оптимальним чи ні.
, то без додаткових досліджень не можна визначити, чи буде він оптимальним чи ні. такий, що вони не можуть бути від’ємними, або їх значення не можуть виходити за межі деякого, визначеного для кожної з них, проміжку. Тобто, у більшості задач лінійного програмування серед обмежень (1.1.2) будуть обмеження виду
такий, що вони не можуть бути від’ємними, або їх значення не можуть виходити за межі деякого, визначеного для кожної з них, проміжку. Тобто, у більшості задач лінійного програмування серед обмежень (1.1.2) будуть обмеження виду  , чи
, чи 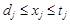 для всіх чи деяких
для всіх чи деяких  .
. , який максимізує лінійну функцію
, який максимізує лінійну функцію
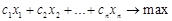 )
)
 …
…  ,
,  .
.
 ,
, ,
,  ,
,  ,
,  ,
, 


 (1.1.7)
(1.1.7) (1.1.8)
(1.1.8)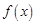 еквівалентна задачі максимізації функції
еквівалентна задачі максимізації функції 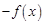 , тобто
, тобто  еквівалентно
еквівалентно 
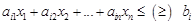
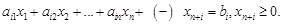
 , причому
, причому 
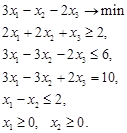
 не визначений, тоді робимо заміну змінної
не визначений, тоді робимо заміну змінної  . У перше, друге та четверте обмеження вводимо додаткові змінні
. У перше, друге та четверте обмеження вводимо додаткові змінні 

 , запаси яких відповідно дорівнюють 300, 450, 260 умовних одиниць, може бути виготовлена продукція двох видів:
, запаси яких відповідно дорівнюють 300, 450, 260 умовних одиниць, може бути виготовлена продукція двох видів:  і
і  . Для виготовлення одиниці продукції
. Для виготовлення одиниці продукції  , 8 одиниць сировини
, 8 одиниць сировини  , 6 одиниць сировини
, 6 одиниць сировини  ; одиниці продукції
; одиниці продукції  35 грн.,
35 грн.,  50 грн.
50 грн. , щоб загальний прибуток був максимальним.
, щоб загальний прибуток був максимальним.
 )
450 (
)
450 ( )
260 (
)
260 ( )
)
 )
8 (
)
8 ( )
6 (
)
6 ( )
)
 )
14 (
)
14 ( )
13 (
)
13 (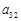 )
)