
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм симплекс-методу та його реалізація за допомогою симплекс-таблицьСодержание книги
Поиск на нашем сайте
Алгоритм симплекс-методу застосовується для КЗЛП:
де Припустимо, що КЗЛП невироджена і ранг матриці Алгоритм симплекс-методу складається з таких процедур: 1. Розкладаються вектори Розклад вектора
Розклад базисних векторів також відомий. Для вектора Розклад інших небазисних векторів знаходиться за формулою:
Позначимо через 2. Для кожного
Якщо всі Якщо є хоча б одна від’ємна оцінка 3. З’ясовуємо, чи існує хоча б одна оцінка Якщо така оцінка існує, тоді цільова функція КЗЛП необмежена зверху на допустимій множині. Кінець алгоритму. Якщо ж таких оцінок немає (тобто для будь-яких 4. Вибираємо одну з Знаходимо мінімальне з цих відношень (нехай це буде
5. Переходимо до нового базисного розв’язку, базис якого отримується заміною вектора Координати усіх векторів
Кожен перехід до нового базису називається ітерацією симплекс-методу. У попередньому розділі було показано, що за скінчену кількість ітерацій алгоритм закінчиться або на 2-му кроці (знайдено оптимальний розв’язок), або на 3-му кроці (з’ясовано, що оптимального розв’язку немає). Зауваження 1. Для виконання першого кроку алгоритму потрібно знати обернену матрицю
Для одиничного базису базисна матриця одинична і обернена тоді також є одиничною. Таким чином, координати будь-якого вектора Зауваження 2. На четвертому кроці алгоритму необхідно вибрати одну з від’ємних оцінок При проведенні розрахунків вручну, пов’язаних з розв’язуванням ЗЛП симплекс-методом, зручно усі обчислення на кожній ітерації записувати у симплекс-таблиці (табл. 1.5): Таблиця 1.5.
Стрілками зверху та зліва відмічені, відповідно, вектор, який потрібно ввести в базис, та вектор, який необхідно вивести з базису, якщо процес не закінчується на даному опорному розв’язку. Приклад 1.9. Розв’язати ЗЛП:
Переходимо до канонічної ЗЛП:
Базисним розв’язком цієї задачі є, наприклад, вектор Очевидно, що ранг матриці
Даний базисний розв’язок невироджений, бо він має 2 додатні координати.
Розкладаємо небазисні вектори
При цьому з базисного розв’язку
Далі заповнюємо таблицю 1.6. Таблиця 1.6.
Початковому базисному розв’язку Підраховуємо відношення:
Заповнюємо симплекс-таблицю, що відповідає новому базисному розв’язку, при цьому координати усіх векторів у новому базисі обчислюємо за правилами, описаними у пункті 1.4.1: Таблиця 1.7.
Оскільки усі оцінки невід’ємні, то останній базисний розв’язок оптимальний:
Приклад 1.10. Розв’язати ЗЛП:
Переходимо до канонічної ЗЛП:
Базисний розв’язок
Таблиця 1.8.
Базисному розв’язку Таблиця 1.9.
Отримали наступний базисний розв’язок Таблиця 1.10.
За даними таблиці 1.10 видно, що виконується критерій оптимальності (всі Економічну інтерпретацію правил симплекс-методу розглянемо на наступному прикладі. Приклад 1.11. Для виробництва трьох видів продукції А, В, С використовується три види ресурсів, запаси яких відповідно дорівнюють 60, 36 та 80 умовних одиниць. Норми витрат ресурсів на одиницю продукції наведено у таблиці 1.11.
Таблиця 1.11.
Ціна одиниці продукції виду А – 10 грн., виду В – 5 грн. та виду С – 12 грн. Знайти оптимальний план виробництва продукції. Побудуємо модель задачі. Змінні
Обмеження задачі пов’язані з витратами ресурсів, тобто
а також невід’ємністю змінних
Розглянемо КЗЛП:
Економічний зміст додаткових невід’ємних змінних Початковий базисний розв’язок задачі -
З економічної точки зору початковий базисний план відповідає ситуації, коли жоден вид продукції не виробляється, запаси ресурсів не використовуються і виручки підприємство не отримує ( Таблиця 1.12.
Від’ємні значення оцінок Від’ємні значення оцінок Так, Те ж саме необхідно зробити і згідно з правилами симплекс-методу. Введення до базису вектора
перше з яких означає скільки можна виробити продукту С, якщо б він вироблявся лише з першого виду ресурсів, друге відношення – якщо б тільки з другого виду ресурсів, третє – з третього. Серед цих величин необхідно вибрати найменшу, тому що другого ресурсу вистачить тільки на 18 одиниць продукції С, тобто В результаті виробництва 18 одиниць продукту С запас другого ресурсу буде повністю використаний, тому змінна Таблиця 1.13.
Наступний базисний план - З економічної точки зору новий план означає, що виробництво продукту виду С у кількості 18 одиниць забезпечить виручку 216 грн. Залишок першого ресурсу – 42 умовні одиниці, третього – 44, а другий ресурс використовується повністю. Якщо у таблиці 1.12 елементи стовпчика Дещо іншу економічну інтерпретацію мають елементи стовпчика З економічної інтерпретації елементів таблиці 1.13 випливає, що знайдений план
На величину випуску продукту Таблиця 1.14
Новий базисний план З економічної точки зору новий план означає, що виробництво продукту А складає 11 одиниць, продукту С – 12,5 одиниць, а продукт В не виробляється. В результаті такого плану другий та третій ресурси витрачаються повністю, а залишок першого ресурсу складає 25,5 умовних одиниць. У порівнянні з попереднім планом виручка зросла на 44 грн. і складає 260 грн. Відсутність від’ємних оцінок
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 762; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

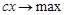 ,
,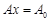 ,
,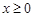 ,
, і
і 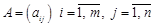 .
. дорівнює
дорівнює 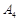 , тобто усі рівняння-обмеження задачі лінійно незалежні. Нехай відомий який-небудь базисний розв’язок
, тобто усі рівняння-обмеження задачі лінійно незалежні. Нехай відомий який-небудь базисний розв’язок  цієї задачі і вектори
цієї задачі і вектори  утворюють базис, так що
утворюють базис, так що  і
і  .
.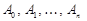 за базисом
за базисом 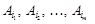 .
. по початковому базису відомий:
по початковому базису відомий: .
. :
:  і
і  .
. ,
, 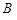 — базисна матриця.
— базисна матриця.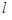 номер ітерації. На першій ітерації
номер ітерації. На першій ітерації  .
. обчислюємо оцінку
обчислюємо оцінку .
. , тоді даний базисний розв’язок оптимальний. Оптимальне значення цільової функції
, тоді даний базисний розв’язок оптимальний. Оптимальне значення цільової функції 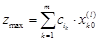 . Кінець алгоритму.
. Кінець алгоритму. , тоді переходимо на 3-й крок.
, тоді переходимо на 3-й крок.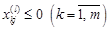 .
. ), тоді переходимо на 4-й крок.
), тоді переходимо на 4-й крок. і підраховуємо відношення
і підраховуємо відношення 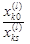 для усіх
для усіх 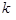 , таких що
, таких що  .
. -те відношення):
-те відношення): .
.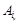 на
на 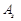 .
. ,
, .
.  . Повертаємося на 2-й крок алгоритму.
. Повертаємося на 2-й крок алгоритму.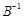 . Доцільно починати симплекс-метод з такого базисного розв’язку, якому відповідає одиничний базис, тобто
. Доцільно починати симплекс-метод з такого базисного розв’язку, якому відповідає одиничний базис, тобто
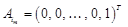 .
.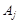 у початковому базисі просто співпадають із складаючими вектор числами
у початковому базисі просто співпадають із складаючими вектор числами  .
.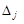 . Якщо таких оцінок декілька, то доцільно вибрати найменшу із них. У більшості випадків це прискорює розв’язування задачі.
. Якщо таких оцінок декілька, то доцільно вибрати найменшу із них. У більшості випадків це прискорює розв’язування задачі.
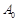


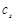
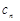
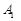
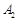
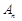
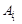
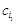
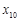
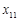



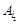
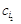

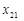
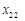
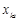



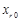







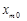

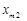
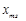
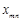

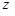




 .
.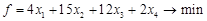 ,
, ,
, ,
, .
. ,
, ,
, ,
, .
. .
.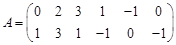 дорівнює 2.
дорівнює 2.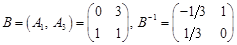 .
. за базисом:
за базисом: ,
, .
.
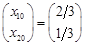 .
.
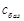

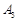
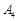


 . Наявність від’ємної оцінки
. Наявність від’ємної оцінки  вказує на можливість збільшення значення цільової функції за умови існування додатних базисних координат вектора
вказує на можливість збільшення значення цільової функції за умови існування додатних базисних координат вектора 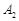 .
. .
.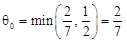 . Отже, з базису виводимо вектор
. Отже, з базису виводимо вектор  . Оптимальне значення цільової функції
. Оптимальне значення цільової функції  .
. ,
, ,
, ,
, .
. ,
, ,
,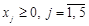 .
. .
. . Враховуючи зауваження 1, заповнюємо таблицю 1.8.
. Враховуючи зауваження 1, заповнюємо таблицю 1.8.

 , якому відповідає значення цільової функції
, якому відповідає значення цільової функції  , що є більшим, ніж при попередньому базисному розв’язку. Однак ще існує можливість його збільшення, якщо ввести до базису вектор
, що є більшим, ніж при попередньому базисному розв’язку. Однак ще існує можливість його збільшення, якщо ввести до базису вектор  . Переходимо до нового базисного розв’язку у таблиці 1.10.
. Переходимо до нового базисного розв’язку у таблиці 1.10.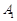
 ). Оптимальним базисним розв’язком є вектор
). Оптимальним базисним розв’язком є вектор  , якому відповідає максимальне значення цільової функції
, якому відповідає максимальне значення цільової функції 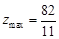 .
. Продукти
Ресурси
Продукти
Ресурси
 , означають кількість продукції відповідно виду А, В та С. Цільову функцію – виручку від реалізації продукції – запишемо так:
, означають кількість продукції відповідно виду А, В та С. Цільову функцію – виручку від реалізації продукції – запишемо так: .
. ,
, ,
, ,
, .
. ,
,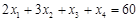 ,
,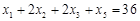 ,
, ,
, .
. - залишки відповідно першого, другого та третього виду ресурсів.
- залишки відповідно першого, другого та третього виду ресурсів. , якому відповідає базис
, якому відповідає базис .
.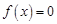 ). Зрозуміло, що така ситуація не може бути найкращою і підтвердженням, з математичної точки зору, цього є від’ємні значення оцінок
). Зрозуміло, що така ситуація не може бути найкращою і підтвердженням, з математичної точки зору, цього є від’ємні значення оцінок  у симплекс-таблиці (табл. 1.12).
у симплекс-таблиці (табл. 1.12).

 з економічної точки зору не тільки свідчать про можливість збільшення загальної виручки, але й показують на скільки збільшиться ця сума при введенні до плану того чи іншого виду продукції.
з економічної точки зору не тільки свідчать про можливість збільшення загальної виручки, але й показують на скільки збільшиться ця сума при введенні до плану того чи іншого виду продукції. означає, що при виробництві одиниці продукції виду А буде забезпечено збільшення виручки на 10 грн. Якщо включити до плану по одному виробу виду В і С, тоді загальна виручка збільшиться відповідно на 5 грн. або 12 грн. Тому з економічної точки зору доцільно включити до плану виробництво саме продукту виду С.
означає, що при виробництві одиниці продукції виду А буде забезпечено збільшення виручки на 10 грн. Якщо включити до плану по одному виробу виду В і С, тоді загальна виручка збільшиться відповідно на 5 грн. або 12 грн. Тому з економічної точки зору доцільно включити до плану виробництво саме продукту виду С. = 60,
= 60,  = 18,
= 18, 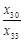 =40,
=40, .
.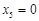 і стає небазисною. Згідно алгоритму симплекс-методу вектор
і стає небазисною. Згідно алгоритму симплекс-методу вектор 

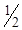
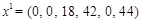 , якому відповідає значення цільової функції
, якому відповідає значення цільової функції 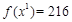 .
. у стовпчику
у стовпчику  . Числа
. Числа 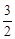 та 4 у першому та третьому рядках стовпчика
та 4 у першому та третьому рядках стовпчика 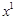 не є оптимальним. Якщо розпочати ще виробництво і продукту виду
не є оптимальним. Якщо розпочати ще виробництво і продукту виду  , де
, де 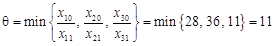 .
.


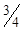


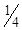
 ,якому відповідає значення цільової функції
,якому відповідає значення цільової функції  .
. говорить про оптимальність останнього плану виробництва продукції, який забезпечує максимальну виручку.
говорить про оптимальність останнього плану виробництва продукції, який забезпечує максимальну виручку.


