
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відношення порядку на множині невід’ємних раціональних чисел.Содержание книги
Поиск на нашем сайте 4. Розглянемо правила порівняння невід’ємних раціональних чисел, причому намагатимемося ввести їх таким чином, щоб вони не суперечили правилам порівняння цілих чисел. Розглянемо спочатку два невід’ємних раціональних числа а= Означення: з двох невід’ємних раціональних чисел з однаковими знаменника меншим (більшим) буде те, у якого чисельник менший (більший). Означення: з двох дробів з різними знаменниками Перше означення символічно можна записати так: ( З’ясуємо, які властивості має це відношення. Оскільки нерівності а<а і а>а не можуть бути одночасно істинними, то це відношення має властивість антирефлексивності. Для виявлення інших властивостей доведемо наступні теореми. Теорема: для будь-яких невід’ємних раціональних чисел Символічно сформульована теорема запишеться так: (" Доведення. За означенням, якщо Теорема: для будь-яких невід’ємних раціональних чисел а, b, с, якщо (а<bÙb<c), то a<c. Символічно ця теорема запишеться так: ("а,b,сєQ0)[(а<bÙb<c)→(a<c)]. Доведення.
Доведені теореми виражають відповідно властивості асиметричності та транзитивності. Таким чином, можна стверджувати, що відношення «менше» («більше») на множині невід’ємних раціональних чисел має властивості антирефлексивності, асиметричності та транзитивності, а тому воно є відношенням строгого порядку.
Додавання і віднімання невід’ємних раціональних чисел. Теореми про існування та єдиність суми і різниці. Властивості (закони) додавання. 5. Однією з умов розширення множини цілих чисел була вимога про необхідність збереження сутності та правил виконання операцій над цілими числами в новій числовій множині. Саме тому, будемо визначати операції над невід’ємними раціональними числами так, щоб це не суперечило правилам виконання цих операцій у попередній числовій множині. Для цього, як ми вже зазначали, кожне ціле число будемо розглядати як дріб із знаменником 1. Оскільки 1+2=3, тобто Означення: сумою двох дробових чисел з однаковими знаменниками є дробове число, чисельник якого дорівнює сумі чисельників, а знаменник – дорівнює їх спільному знаменнику. Наприклад, Означення: сумою двох невід’ємних раціональних чисел У жодному з означень нічого не говориться про існування та єдиність суми невід’ємних раціональних чисел. Саме тому слід довести відповідні теореми. Теорема: сума невід’ємних раціональних чисел існує і єдина. Доведення. Розглянемо два дроби Для того, щоб одержати відповідь на запитання: «чи підкоряється операція додавання невід’ємних раціональних чисел комутативному та асоціативному законам?», необхідно довести відповідні теореми. Теорема: операція додавання в множині невід’ємних раціональних чисел підкоряється комутативному та асоціативному законам. Символічно вони запишуться так: (" Доведення. Розглянемо три дробових числа, але для спрощення викладок виберемо їх із спільними знаменниками, Означення: сума натурального числа і дробового числа, записаних поряд без знака додавання називають мішаним числом. Наприклад, 8+ Операцію віднімання у множині невід’ємних раціональних чисел також означатимемо так, щоб це не суперечило правилам віднімання цілих чисел. Означення: відняти від дробового числа Таке означення не суперечить тому, яке ми прийняли для невід’ємних цілих чисел. Для того, щоб знайти різницю двох дробових чисел, приймемо наступне означення. Означення: різницею двох дробових чисел з рівними знаменниками називається таке третє дробове число, чисельник якого дорівнює різниці чисельників, а знаменник – спільному знаменнику. Символічно прийняте означення запишеться так: Теорема: різниця двох невід’ємних раціональних чисел Доведення. Для спрощення викладок розглядатимемо дроби з однаковими знаменниками. Оскільки у формулюванні теореми є словосполучення «тоді і тільки тоді», то доведення складатиметься з двох частин: 1) якщо різниця Доведемо першу частину. Оскільки різниця Теорема: якщо різниця невід’ємних раціональних чисел існує, то вона єдина. Доведення цієї теореми пропонуємо провести методом від супротивного самостійно.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 з однаковими знаменниками. Будемо вважати, що
з однаковими знаменниками. Будемо вважати, що  . Як же бути у випадку дробів з різними знаменниками? Для відповіді на поставлене запитання приймемо наступні означення.
. Як же бути у випадку дробів з різними знаменниками? Для відповіді на поставлене запитання приймемо наступні означення. меншим (більшим) буде той, для якого справджується нерівність pk<qn (pk>qn).
меншим (більшим) буде той, для якого справджується нерівність pk<qn (pk>qn). )Û(pk>qn).
)Û(pk>qn). і
і  , якщо
, якщо 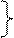 Розглянемо невід’ємні раціональні числа такі, що
Розглянемо невід’ємні раціональні числа такі, що  . Тоді маємо:
. Тоді маємо: 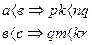 →pk<nq<qm<kr→pm<nr→
→pk<nq<qm<kr→pm<nr→  <
<  →a<c. Що й треба було довести.
→a<c. Що й треба було довести. , то
, то  +
+  =
=  =
=  . Прийняте означення можна поширити на будь-яку скінченну кількість доданків, наприклад:
. Прийняте означення можна поширити на будь-яку скінченну кількість доданків, наприклад:  . Як же бути в тому випадку, коли дроби мають різні знаменники? – звести їх до спільного знаменника і додати за попереднім означенням. Можна прийняти і наступне означення.
. Як же бути в тому випадку, коли дроби мають різні знаменники? – звести їх до спільного знаменника і додати за попереднім означенням. Можна прийняти і наступне означення. називається третє невід’ємне раціональне число
називається третє невід’ємне раціональне число 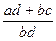 , тобто
, тобто  =
= 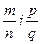 такі, що m і р єZ0, а n і qєN. Знайдемо їх суму.
такі, що m і р єZ0, а n і qєN. Знайдемо їх суму.  =
=  - згідно означення. Тоді mqÎZ0, pnÎZ0 і nqÎZ0, а тому одержаний нами дріб
- згідно означення. Тоді mqÎZ0, pnÎZ0 і nqÎZ0, а тому одержаний нами дріб 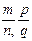 єQ0)(
єQ0)( ); ("
); ("  єQ0)((
єQ0)((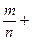
 )+
)+  )).
)). і доведемо, що (
і доведемо, що ( ). (
). ( =(Чому?!)=
=(Чому?!)=  (Чому?!)=
(Чому?!)=  (Чому?!)=
(Чому?!)=  . Отже, (
. Отже, ( ) сполучний закон додавання невід’ємних раціональних чисел доведено.
) сполучний закон додавання невід’ємних раціональних чисел доведено. =8
=8  =
= 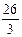 . Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад:
. Щоб перетворити неправильний дріб у мішане число, потрібно поділити чисельник на знаменник і частку записати перед дробом, а остачу записати у чисельнику, залишивши той самий знаменник, наприклад: 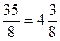 . Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання.
. Отже, множина невід’ємних раціональних чисел замкнена відносно операції додавання. . Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так:
. Щоб знайти різницю дробових чисел з різними знаменниками, слід звести їх до спільного знаменника та використати попереднє означення. Символічно це запишеться так:  . У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.
. У прийнятих означеннях нічого не говориться про існування та єдиність різниці. Саме тому слід довести наступні теореми.



