

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Модуль іу. «системи числення. Подільність чисел. ».
Содержание книги
- Розподіл годин по семестрах для спеціальності 6. 010102- початкове навчання.
- Теми практичних занять для спеціальності 6.010102 –початкова освіта (2 р.н.).
- Навчальний проект для спеціальності 6.010102 – початкова освіта
- Для особистого контролю за одержанням балів
- Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.
- Операція перетину множин та основні властивості (закони) цієї операції.
- Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.
- Малюнок № 1. 19. Задання декартового добутку множин за допомогою графа.
- Малюнок № 1.20. Граф відповідності.
- Розміщення з повтореннями та без повторень.
- Перестановки з повтореннями та без повторення.
- Поняття як форма мислення, зміст і обсяг поняття та зв'язок між ними.
- Діаграма № 2.1. Відношення часткового збігу між поняттями.
- Поняття предиката, його позначення та область визначення. Поняття кванторів існування та загальності, їх позначення та зв'язок між ними.
- Операція кон'юнкції предикатів.
- Операція еквіваленції предикатів.
- Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
- Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Аксіоматичне означення додавання цілих невід’ємних чисел в аксіоматичній теорії. Таблиці і закони додавання.
- Порівняння відрізків, дії над відрізками. Натуральне число як результат вимірювання величини. Натуральне число як міра величини. Натуральне число як міра відрізка.
- Означення операцій додавання і віднімання чисел, що розглядаються як міри відрізків. Трактування множення і ділення, які розглядаються як міри відрізків.
- Позиційні та непозиційні системи числення, запис чисел у позиційних і непозиційних системах числення.
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- Модуль іу. «системи числення. Подільність чисел. ».
- Загальна ознака подільності Б. Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Основна теорема арифметики цілих невід’ємних чисел.
- Обчислення нсд і нск способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
- Ознаки подільності на складені числа.
- Відношення порядку на множині невід’ємних раціональних чисел.
- Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
- Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
- Множина раціональних чисел, модуль раціонального числа, операції над раціональними числами. Властивості множини раціональних чисел.
- Відношення порядку на множині дійсних чисел.
- Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
- Тотожні перетворення виразів. Тотожності. Виведення основних тотожностей.
- Рівносильні рівняння. Теореми про рівносильність рівнянь.
- Рівняння з двома змінними. Рівняння лінії. Рівняння прямої та їх види.
- Малюнок № 6.1. Графік рівняння кола.
- Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.
- Застосування рівнянь та їх систем до розв’язування текстових задач.
- Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.
- Обернена пропорційність, її властивості та графік.
- Основні геометричні побудови циркулем і лінійкою.
- Побудова прямої, яка проходить через дану на ній точку, перпендикулярно до даної прямої.
- Побудова правильних многогранників.
- Правильні многогранники та їх види.
- Модуль 7: «елементи геометрії. Величини. ».
Змістовний модуль 4.2. «Подільність цілих невід’ємних чисел.».
ПЛАН.
1. Поняття «відношення подільності» та його властивості.
2. Теореми про подільність суми, різниці і добутку цілих невід’ємних чисел на натуральні числа.
3. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
4. Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
5. Основна теорема арифметики цілих невід’ємних чисел.
6. Дільники і кратні. Спільні дільники і спільні кратні. Найбільший спільний дільник (НСД) і найменше спільне кратне (НСК), їх властивості.
7. Обчислення НСД і НСК способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
8. Загальна ознака подільності Б.Паскаля. Ознаки подільності на складені числа.
ЛІТЕРАТУРА: [1] – с. 141-155; [2] – с. 162-192; [3] – с. 271-289.
Поняття «відношення подільності» та його властивості.
1. Розглядаючи теоретико-множинну теорію цілих невід’ємних чисел, ми ввели означення відношення “ділитися націло”, розглянули його властивості. Як відомо, поділити ціле невід’ємне число а на натуральне число b це означає знайти таке ціле невід’ємне число с, що виконується рівність а=сb.
Означення: якщо для ає 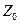 і bÎ і bÎ 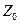 існує таке сÎ існує таке сÎ 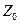 , що виконується рівність а=сb, то говорять, що числа а і b знаходяться у відношенні подільності. , що виконується рівність а=сb, то говорять, що числа а і b знаходяться у відношенні подільності.
Означення: натуральне число а ділиться націло на натуральне число b, якщо існує додатній цілий корінь рівняння b×х=а.
Означення: натуральне число а не ділиться націло на натуральне число b, якщо не існує натурального кореня рівняння b×х=а.
Для позначення відношення подільності використовується такий символічний запис a  b, який можна читати так: числа а і b знаходяться у відношення подільності, або а кратне b, або а ділиться націло на b, або b є дільником числа а. Відношення “ділитися націло” на множині цілих невід’ємних чисел є відношенням нестрогого порядку, бо володіє властивостями рефлексивності, антисиметричності та транзитивності. На основі цього відношення доводиться ряд теорем. b, який можна читати так: числа а і b знаходяться у відношення подільності, або а кратне b, або а ділиться націло на b, або b є дільником числа а. Відношення “ділитися націло” на множині цілих невід’ємних чисел є відношенням нестрогого порядку, бо володіє властивостями рефлексивності, антисиметричності та транзитивності. На основі цього відношення доводиться ряд теорем.
Теореми про подільність суми, різниці і добутку цілих невід’ємних чисел на натуральні числа.
2. Розглянемо деякі теореми, що дозволять давати відповідь на запитання про подільність найпростіших виразів на число.
Теорема 1: якщо кожен доданок суми цілих невід’ємних чисел ділиться на деяке натуральне число, то і сума цих чисел поділиться на це натуральне число.
Доведення: доведення проведемо для випадку двох доданків. Розглянемо цілі невід’ємні числа aÎ 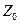 , bÎ , bÎ 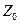 , сÎN, a+bÎ , сÎN, a+bÎ 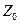 . Нехай за умовою теореми . Нехай за умовою теореми 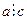 , ,  . Спробуємо довести, що (a+b) . Спробуємо довести, що (a+b)  c. За означенням відношення подільності, якщо c. За означенням відношення подільності, якщо 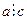 , ,  , то існують такі к,mєN, що справедливі рівності а=с·к і в=с·m. Тоді а+в=ск+сm=с(к+m) (за дистрибутивним законом). Отже, a+b=c(k+m). Оскільки k, mÎ , то існують такі к,mєN, що справедливі рівності а=с·к і в=с·m. Тоді а+в=ск+сm=с(к+m) (за дистрибутивним законом). Отже, a+b=c(k+m). Оскільки k, mÎ 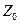 , то (k+m)Î , то (k+m)Î 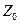 . Таким чином, a+b=c(k+m). Тоді (a+b) . Таким чином, a+b=c(k+m). Тоді (a+b)  c. Теорема доведена. c. Теорема доведена.
Доведену теорему можна поширити на будь-яке скінченне число доданків. Виявляється, що доведена теорема є лише достатньою ознакою подільності суми на число. Сформулюємо необхідну і достатню ознаку подільності суми на число, яку приймемо без доведення. Ознака: якщо один із кількох доданків суми цілих невід’ємних чисел ділиться на дане число, то для того, щоб сума ділилась на це число, необхідно і достатньо, щоб і кожен із решти доданків ділився на це число.
Теорема 2: якщо зменшуване і від’ємник різниці двох цілих невід’ємних чисел діляться на дане натуральне число, то і різниця поділиться на це натуральне число. – доведення цієї теореми пропонуємо провести самостійно, використовуючи доведення попередньої теореми!
Теорема 3: Добуток цілих невід’ємних чисел ділиться на натуральне число тоді, коли на дане число ділиться хоча б один із співмножників.
Доведення: для спрощення викладок доведення теореми проведемо для випадку двох співмножників. Нехай дано добуток цілих невід’ємних чисел ab. Виберемо для визначеності, що 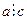 . Доведемо, що тоді . Доведемо, що тоді  c. Оскільки c. Оскільки 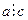 , то за означенням відношення подільності маємо а=ск, де кє , то за означенням відношення подільності маємо а=ск, де кє 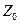 . Отже, ав=(ск)в=с(кв). Оскільки . Отже, ав=(ск)в=с(кв). Оскільки 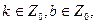 то то  , тому (ab) , тому (ab)  c. Теорему доведено. c. Теорему доведено.
|