

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
Содержание книги
- Теми практичних занять для спеціальності 6.010102 –початкова освіта (2 р.н.).
- Навчальний проект для спеціальності 6.010102 – початкова освіта
- Для особистого контролю за одержанням балів
- Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.
- Операція перетину множин та основні властивості (закони) цієї операції.
- Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.
- Малюнок № 1. 19. Задання декартового добутку множин за допомогою графа.
- Малюнок № 1.20. Граф відповідності.
- Розміщення з повтореннями та без повторень.
- Перестановки з повтореннями та без повторення.
- Поняття як форма мислення, зміст і обсяг поняття та зв'язок між ними.
- Діаграма № 2.1. Відношення часткового збігу між поняттями.
- Поняття предиката, його позначення та область визначення. Поняття кванторів існування та загальності, їх позначення та зв'язок між ними.
- Операція кон'юнкції предикатів.
- Операція еквіваленції предикатів.
- Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
- Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Аксіоматичне означення додавання цілих невід’ємних чисел в аксіоматичній теорії. Таблиці і закони додавання.
- Порівняння відрізків, дії над відрізками. Натуральне число як результат вимірювання величини. Натуральне число як міра величини. Натуральне число як міра відрізка.
- Означення операцій додавання і віднімання чисел, що розглядаються як міри відрізків. Трактування множення і ділення, які розглядаються як міри відрізків.
- Позиційні та непозиційні системи числення, запис чисел у позиційних і непозиційних системах числення.
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- Модуль іу. «системи числення. Подільність чисел. ».
- Загальна ознака подільності Б. Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Основна теорема арифметики цілих невід’ємних чисел.
- Обчислення нсд і нск способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
- Ознаки подільності на складені числа.
- Відношення порядку на множині невід’ємних раціональних чисел.
- Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
- Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
- Множина раціональних чисел, модуль раціонального числа, операції над раціональними числами. Властивості множини раціональних чисел.
- Відношення порядку на множині дійсних чисел.
- Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
- Тотожні перетворення виразів. Тотожності. Виведення основних тотожностей.
- Рівносильні рівняння. Теореми про рівносильність рівнянь.
- Рівняння з двома змінними. Рівняння лінії. Рівняння прямої та їх види.
- Малюнок № 6.1. Графік рівняння кола.
- Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.
- Застосування рівнянь та їх систем до розв’язування текстових задач.
- Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.
- Обернена пропорційність, її властивості та графік.
- Основні геометричні побудови циркулем і лінійкою.
- Побудова прямої, яка проходить через дану на ній точку, перпендикулярно до даної прямої.
- Побудова правильних многогранників.
- Правильні многогранники та їх види.
- Модуль 7: «елементи геометрії. Величини. ».
- Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
Похожие статьи вашей тематики
1. У математиці під числовою алгеброю розуміють таку алгебру, основою множиною якої є числа і букви (під якими розуміють числа), основними операціями якої є додавання, віднімання, множення і ділення. З елементів основної множини за допомогою операцій утворюють інші елементи числової алгебри, а за допомогою основних операцій визначають інші нові операції, вводячи для них нові позначення.
Мова будь-якої алгебри складається з множини знаків, яку називають алфавітом цієї мови. Числова алгебра містить десять букв, які прийнято називати цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. За допомогою цифр згідно з певними правилами утворюються назви будь-яких чисел. Для позначення числових змінних використовують букви латинського алфавіту a, b, c, …, x, y, z або деякі з цих букв з індексами 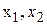 ... Інколи букви латинського алфавіту використовуються і для позначення числових сталих, тобто для позначення назв чисел. Для позначення певного конкретного, але не важливо якого числа, використовуються початкові букви латинського алфавіту a, b, c, …, а останніми буквами латинського алфавіту позначають змінні. ... Інколи букви латинського алфавіту використовуються і для позначення числових сталих, тобто для позначення назв чисел. Для позначення певного конкретного, але не важливо якого числа, використовуються початкові букви латинського алфавіту a, b, c, …, а останніми буквами латинського алфавіту позначають змінні.
Для позначення операцій використовують відомі знаки „+”, „-”, „  ”, „:”, а крім цього для запису чисел можуть використовувати праву „(” і ліву „)” дужки. Таким чином, алфавіт мови, на якій описується будь-яка числова алгебра, повинен включати таку множину: А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +. -, ´, ·,:, (,)}. Із елементів множини А утворюють скінченні послідовності цифр і букв, які називають виразами. Однак, так само як і в українській мові, не кожна послідовність цифр і букв алфавіту А утворює вираз. Наприклад, послідовність 5-) не є виразом. Саме тому постає питання про визначення поняття „вираз”. Хоча це поняття є одним з основних понять математики, зазначимо, що не існує загальноприйнятого означення поняття „вираз”. Саме тому наведемо індуктивне означення поняття „вираз”, в якому: 1) перераховуються елементарні вирази; 2) формулюються правила утворення нових виразів, із тих, що вже є; 3) стверджується, що інших виразів, крім тих, які можуть бути утворені у відповідності з першими двома пунктами визначення, не існує. ”, „:”, а крім цього для запису чисел можуть використовувати праву „(” і ліву „)” дужки. Таким чином, алфавіт мови, на якій описується будь-яка числова алгебра, повинен включати таку множину: А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +. -, ´, ·,:, (,)}. Із елементів множини А утворюють скінченні послідовності цифр і букв, які називають виразами. Однак, так само як і в українській мові, не кожна послідовність цифр і букв алфавіту А утворює вираз. Наприклад, послідовність 5-) не є виразом. Саме тому постає питання про визначення поняття „вираз”. Хоча це поняття є одним з основних понять математики, зазначимо, що не існує загальноприйнятого означення поняття „вираз”. Саме тому наведемо індуктивне означення поняття „вираз”, в якому: 1) перераховуються елементарні вирази; 2) формулюються правила утворення нових виразів, із тих, що вже є; 3) стверджується, що інших виразів, крім тих, які можуть бути утворені у відповідності з першими двома пунктами визначення, не існує.
Означення: 1. Кожна окрема цифра або буква латинського алфавіту є виразом. Такі вирази називаються елементарними. 2. Якщо 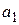 і і 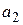 вирази, то вирази, то  і і 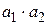 – також вирази. 3. Інших виразів, крім тих, які можуть бути одержані у відповідності з пп. 1.2, не існує. – також вирази. 3. Інших виразів, крім тих, які можуть бути одержані у відповідності з пп. 1.2, не існує.
Для спрощення запису виразів прийняли такі домовленості:
а) опускати зовнішні дужки, які містять всередині себе всі решта букв, які складають вираз;
б) у виразі повинна бути однаковою кількість правих і лівих дужок;
в) вважати, що знак множення пов’язує сильніше, ніж знак додавання.
Наведене означення виразу та прийняті домовленості щодо правил запису виразів дозволяють відносно будь-якої послідовності цифр чи букв встановити чи є вона виразом, чи ні. Покажемо це на наступному прикладі.
Вправа: встановити чи є виразами такі послідовності букв: 1) (((3+b)●3))+(4●у)); 2) (((7+а)●3+(8●а)).
Розв’язання:
Перевіряємо, чи є у послідовностях зовнішні дужки, які містять всередині себе весь запис. Отже, у кожному з наведених записів слід опустити по одній зовнішній дужці. Оскільки у першому виразі є 4 лівих і 5 правих дужок, то такий запис не є виразом, бо не виконується друга домовленість. Аналогічно і другий запис не є виразом. Відповідно до третьої вимоги, слід опустити дужки, в яких стоїть лише дія множення. Таким чином, для того, щоб вказані записи були виразами, записи слід представити так: 1) (3+b)●3+4●у; 2) (7+а)●3+8●а.
У математиці існують різні класифікації виразів. Відповідно до однієї з них всі вирази поділяють на числові та нечислові. Щоб зрозуміти цю класифікацію приймемо наступне означення.
Означення: вираз, який не містить змінних, тобто складається тільки з цифр, знаків операцій і можливо дужок, називається числовим виразом.
Наприклад: “7”, (2+8)●7-5.
Всякий числовий вираз пов’язаний з деяким число, яке ми одержимо, якщо виконаємо відповідні дії над числами. Це число називається значенням числового виразу. Так, наприклад значенням виразу “3” є число 3, а значенням числового виразу (8-3)●3 є число 15. Зазначимо, що існують числові вирази, які у певній числовій множині не мають числового значення. Наприклад, вираз (5-3):3 у множні натуральних чисел немає числового значення, але в множині раціональних чисел його числовим значенням є число ⅔. Щоб знайти числове значення виразу, пропонуємо самостійно виконати наступну вправу.
Вправа: знайти числове значення виразу 27:(72-72). Що можна сказати про числове значення цього виразу?
|