
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення термічного коефіцієнта тиску повітря за допомогою газового термометраСодержание книги
Поиск на нашем сайте ПЕРЕДМОВА У даних вказівках наведено опис лабораторних робіт, що виконуються студентами 1 курсу всіх спеціальностей у лабораторії “Молекулярна фізика” Харківської національної академії міського господарства. У них міститься необхідна інформація щодо підготовки, виконання та звітності про лабораторну роботу. На відміну від механіки, що вивчає рух тіл під дією сил, молекулярна фізика вивчає будову і властивості речовини, виходячи із молекулярно-кінетичних уявлень. Згідно з цими уявленнями будь-яка речовина складається з великої кількості мікроскопічних частинок (молекул, атомів), що знаходяться в хаотичному неперервному русі. Вказана теорія описує ті властивості тіл, які проявляються в дослідах (тиск, температура, об’єм) як результат дії молекул. При цьому використовується статистичний метод, тобто вивчається поведінка не окремої молекули, а їх великої сукупності. Вивченням різних властивостей і змін стану речовини займається також термодинаміка, яка, не розглядаючи мікроскопічні процеси дає висновки відносно їх протікання. Статистична фізика і термодинаміка взаємно доповнюють одна одну, утворюючи одне ціле. Головною метою вказівок є намір не тільки всебічно проілюструвати фізичні явища і закони, але й навчити студента їх спостерігати і перевіряти дослідним шляхом. Вони мають сприяти оволодінню технікою фізичного експерименту, отриманню навичок самостійної дослідницької роботи і виробленню вмінь застосовувати теоретичні знання для аналізу і розв’язання в майбутньому конкретних інженерних задач. Представлені різні варіанти вимірювань однієї і тієї ж величини, завдяки чому студент отримує уявлення про розмаїття методів фізичних досліджень. У кожній лабораторній роботі подається короткий виклад понять, законів, явищ та фізичної основи використаного методу. При цьому передбачається самостійне вивчення підручника, оскільки лабораторна робота може виконуватися студентом ще до прочитання відповідної лекції. Особлива увага надається безпосереднім вимірюванням та обробці результатів. Щоб правильно оцінити їх надійність і точність, необхідно мати чітке уявлення про розмірність досліджуваної величини, знати правила користування основними обчислювальними і вимірювальними приладами, а також основи теорії похибок. При підготовці до лабораторної роботи студент повинен вивчити ці методичні вказівки, а також відповідні теоретичні положення, користуючись підручником чи конспектом лекцій. Як основний підручник рекомендується "Курс загальної фізики" І.В.Савельєва. т.1 за 1973 – 1985 рр. Методичні вказівки узагальнюють надбання співробітників кафедри фізики ХНАМГ, які протягом багатьох попередніх років робили певний внесок у створення лабораторного практикуму, що відповідає в повному обсязі програмі курсу фізики для технічних вузів. Вони написані з урахуванням досвіду методичного забезпечення лабораторного практикуму у вищих навчальних закладах України. Лабораторна робота 16 ВИЗНАЧЕННЯ ТЕРМІЧНОГО КОЕФІЦІЄНТА ТИСКУ ПОВІТРЯ ЗА ДОПОМОГОЮ ГАЗОВОГО ТЕРМОМЕТРА Мета роботи: вивчити закони для ідеальних газів; перевірити закон Шарля. 1. Обладнання: 1.1. Газовий термометр. 1.2. Нагрівач. 1.3. Термометр кімнатний. 1.4. Барометр. Загальні положення Ідеальний газ – це модель газу: його молекули не взаємодіють між собою і мають розміри, якими можна знехтувати. При зіткненнях молекули ідеального газу поводять себе як абсолютно пружні кулі з діаметром σ (ефективний діаметр молекули), який залежить від хімічної природи газу. У реальних газах взаємодія між молекулами має такий характер: на відстанях порядка розміру молекули (~ 10–10 м) це дуже сильне відштовхування, яке при збільшенні відстані змінюється швидко спадаючим притяганням. На відстанях ~ 10–9 м молекули практично не взаємодіють. Отже, реальні гази при малій густині можуть вважатися ідеальними. Стан ідеального газу довільної маси m описується рівнянням Менделєєва – Клапейрона
де μ – молярна маса газу; R – універсальна газова стала; P, V, T – відповідно, тиск, об’єм та температура газу. Розглянемо це рівняння для 1 моля газу. Вважаючи тиск постійним, беремо диференціали від обох частин: P dV = R dT. Але P dV = dA – це робота газу при збільшенні об’єму на dV. Отже універсальна газова стала R чисельно дорівнює роботі при ізобаричному розширенні 1 моля газу внаслідок його нагрівання на 1 К. В одиницях СІ R = 8,31 Дж/моль·К. Для ідеальних газів діють такі закони: 1. Закон Бойля-Маріотта: при T = const (ізотермічний процес)та P V = const. (2.2) 2. Закон Гей-Люссака: при P = const (ізобарний процес)об’єм даної маси газу прямо пропорційний його абсолютній температурі
де Vo – об’єм газу при температурі To = 273, 15 К, t – температура за шкалою Цельсія, aV = 3. Закон Шарля: при V = const (ізохорний процес) тиск даної маси газу прямо пропорційний абсолютній температурі
де Po – об’єм газу при температурі To = 273,15 К; aР = 4. Закон Авогадро: при однакових тисках та температурах в рівних об’ємах довільного газу міститься однакова кількість молекул. Порядок виконання роботи 4.1. Переміщуючи праве коліно манометра, встановити рівень ртуті на рівень позначки 3. Провести підрахунок h з точністю до 0,5 МПа. 4.2. Розмістити балон 1 у нагрівачі. У процесі нагрівання підтримувати рівень ртуті в лівому коліні в початковому положенні. Коли газ прийме температуру t 2 (температура пари киплячої води), виконати заміри показників манометра h 2. 4.3. Вимкнути нагрівач і, пересуваючи вниз правий повзунок, опустити праве коліно манометра для того, щоб при охолодженні газу ртуть не засмоктало в балон. 4.4. Виміряти барометром атмосферний тиск Р атм. 4.5. Визначити початковий Р 1 і кінцевий Р 2 тиск газу за формулою (3.1) і обчислити величину a Р згідно з формулою (3.4). 4.6. Визначити абсолютну й відносну похибку визначення D a Р, вважаючи що a = f (Ратм, h1, h2, t1, t2). Результати записати в табл. 4.1. Таблиця 4.1
5. Контрольні запитання 1. Що називається термічним коефіцієнтом тиску? Які одиниці його вимірювання в СІ? 2. Суть закону Шарля. 3. Як дізнатися, що повітря в балоні нагрівають до температури кипіння води? 4. Чи є один газ кращим, ніж інший, для побудови газового термометра? 5. Чому не використовуються водяні термометри? Лабораторна робота 17 Загальні положення Якщо існує просторова неоднорідність густини, температури газу (рідини), або швидкості руху окремих його шарів, то виникає впорядкований перенос, відповідно, маси (дифузія), внутрішньої енергії (теплопровідність) і імпульсу (внутрішнє тертя). Ця група процесів об’єднується назвою явища переносу. В результаті зіткнень між молекулами газу (рідини) відбуваються безперервні зміни їх швидкостей та енергій. Отже, тепловий рух є хаотичним. Якщо виділити напрямок Х і обрати перпендикулярно ньому поверхню D S, то в разі відсутності неоднорідностей через неї по і протилежно Х буде проходити в середньому одна й та сама кількість молекул, які будуть переносити в середньому однакову енергію і імпульс. Ця динамічна рівновага буде зберігатися доти, доки зовнішнє втручання в систему не призведе до втрати однорідності.
Розглянемо найпростіший випадок, коли величини змінюються тільки вздовж одного напрямку, Х. Оберемо дві однакові перпендикулярні до Х поверхні D S1 і D S2, розташовані на відстані Δ х одна від одної. Будемо вважати, що зліва від D S1 величини більші, ніж справа від D S2 (рис. 2.1). Тепер можемо переходити до виведення дуже схожих між собою рівнянь для явищ переносу. 2.1. Дифузія – процес вирівнювання густини молекул газу (рідини) або встановлення рівноважного розподілу концентрацій. Кількість молекул, які пройдуть через поверхню D S1 у напрямку Х буде тим більша, чим більші час спостереження Δ t, кількість молекул в одиниці об’єму n зліва від неї, а також площа цієї поверхні. Ті самі міркування справедливі і щодо кількості молекул, що пройдуть через поверхню D S2 протилежно Х. Але не всі молекули, що покидають D S1 встигнуть за час Δ t досягти D S2. Припустимо, середня швидкість молекул в напрямку Х дорівнює V. Тоді молекула проходить відстань Δ х в середньому за час
де m0 маса однієї молекули, k – коефіцієнт, що залежить лише від властивостей газу чи рідини. Густина потоку молекул при дифузії – це кількість молекул, що проходять через одиницю поверхні за одиницю часу. Цю величину легко отримати з рівняння (2.1), якщо перейти в ньому до похідних і поділити обидві частини на m0:
мінус з’являється, бо ми врахували напрямок зміни концентрації, D – коефіцієнт дифузії. Рівняння (2.2) називається законом Фіка. При виведенні (2.2) ми бачили, що коефіцієнт дифузії пропорційний середній швидкості вздовж деякого напрямку. Згадаємо тепер, що молекули в рідині або газі постійно стикаються між собою, при цьому напрямок і величина швидкостей суттєво змінюються. Середня довжина, яку проходять молекули між послідовними зіткненнями, називається середньою довжиною вільного пробігу λ. Зрозуміло, що чим частіше стикаються молекули, тим повільніше буде йти процес дифузії. Отже, коефіцієнт дифузії має бути тим більшим, чим більше λ. В кінетичній теорії газів отримана формула:
де 2.2. Явище теплопровідності полягає в переносі деякої кількості тепла D Q від більш гарячого шару до більш холодного. Як відомо, температура газу (рідини) прямо пропорційна квадрату середньої швидкості його молекул, тобто їх середній кінетичній енергії. Знову скористаємося рис. 2.1. Молекули з області зліва від D S1, яка є більш нагрітою, переходять в область справа від D S2. Будемо вважати, що не відбувається впорядкованого руху молекул (тобто обидві поверхні в середньому перетинає однакова кількість молекул). Тоді кількість тепла, перенесена з більш нагрітої області до менш нагрітої за час Δ t дорівнює різниці перенесеної кінетичної енергії, яка в свою чергу дорівнює різниці температур. Отже,
де К – коефіцієнт теплопровідності. Диференціальна форма цього рівняння:
де q – питомий тепловий потік, кількість теплоти, що передається через перпендикулярну Х одиничну плоску поверхню за одиницю часу. Рівняння (2.4) називається законом Фурьє. Згідно з молекулярно–кінетичною теорією коефіцієнт теплопровідності
де сV – питома теплоємність газу (рідини) при постійному об’ємі, ρ – густина. 2.3. Внутрішнє тертя виникає між двома шарами газу або рідини, що переміщуються паралельно один одному з різними за величиною швидкостями. Причиною внутрішнього тертя є перенос молекулами кількості руху від одного шару газу або рідини до іншого. Припустимо, шар газу (рідини) А рухається зі швидкістю
де
Повторюючи міркування п.п. 1-2, маємо формулу:
де η – коефіцієнт внутрішнього тертя. Відповідно до кінетичної теорії,
Отже, дія сил внутрішнього тертя проявляється в зменшенні відносної швидкості шарів, тобто той з них, що рухався повільніше, прискорюється, а більш швидкий уповільнюється. До того ж, сумарний імпульс нашої системи весь час зменшується, бо зростає енергія хаотичного руху молекул, тобто, як відомо, тертя призводить до нагрівання. В диференціальній формі формула (2.6) має вигляд (знову врахування напрямку зміни величини, в цьому випадку, швидкості, дає знак „мінус”):
де τ – сила, що діє на одиницю площі. Ця величина називається напруженістю тертя, а закон (2.8) є законом Ньютона для явища внутрішнього тертя. Лабораторна робота № 18 Загальні положення Модуль сили внутрішнього тертя, прикладеної до площі S поверхні шару газу (рідини), визначається формулою
де η – коефіцієнт внутрішнього тертя, який залежить від природи і стану речовини (наприклад, температури); Лабораторна робота № 19 Метод Стокса Плин рідини, при якому шари рідини (газу) сковзають упорядковано й плавно уздовж так званих ліній струму, називається ламінарним. Якщо ж плин є неупорядкованим і містить завихрення, він називається турбулентним. В'язкість визначає внутрішнє тертя, що перешкоджає вільному плину рідини. В’язке тертя можна уявити собі як тертя між суміжними шарами рідини, що рухаються відносно один одного. На тіло, що рухається равномірно у в’язкій рідини, діє сила внутрішнього тертя. Потік, що обтікає тіло, є ламінарним; дослідним шляхом було з’ясовано, що сила внутрішнього тертя F v прямо пропорційна швидкості об'єкта:
Значення коефіцієнта k залежить від розмірів і форми тіла, а також від в'язкості рідини (газу). ЗокремаСтокс теоретично показав, що при падінні кульки в безмежній рідині, якщо при цьому не виникає завихрень (падіння маленької кульки з малою швидкістю), сила тертя, яка діє на неї, виражається формулою
На тверду кульку у в’язкій рідині діють три сили: сила тяжіння
де ρ1 – густина рідини; ρ – густина кульки. При русі кульки шар рідини, що межує з її поверхнею, прилипає до неї і рухається із швидкістю кульки. Найближчі суміжні шари рідини також починають рухатися. Одержувана ними швидкість тим менша, чим далі вони знаходяться від кульки. Таким чином, при обчисленні опору середовища необхідно враховувати тертя окремих шарів рідини між собою, а не тертя між кулькою і рідиною. У випадку падіння кульки всі сили спрямовані по вертикалі: сила тяжіння – донизу; виштовхувальна сила й сила опору – догори. Сила опору f через велику початкову швидкість кульки спочатку є максимальною. З часом рух кульки сповільнюється і досягає такої швидкості, при якій всі три сили будуть врівноважені. Такий рух називається стаціонарним. При цьому кулька рухається по інерції з постійною швидкістю v o. Для цього випадку маємо:
Розв’язуючи рівняння (2.3) відносно коефіцієнта внутрішнього тертя η, одержуємо:
де S – шлях, який кулька пройшла за τ секунд. Реалізувати падіння кульки в безмежному середовищі в лабораторних умовах практично неможливо, оскільки рідина завжди міститься в якій-небудь посудині, що має стінки. Урахування наявності стінок при русі кульки вздовж осі циліндра приводить до виразу
де D – діаметр поперечного перерізу циліндра; d – діаметр кульки. Коефіцієнт внутрішнього тертя залежить від температури. У зв’язку в цим, записуючи значення коефіцієнта внутрішнього тертя досліджуваної рідини, необхідно вказувати температуру. Значенння температури вимірюють за допомогою лабораторного термометра. Метод Оствальда Ідея цього методу полягає у порівнянні часу витікання τ1 і τ2 рівних об’ємів рідин – еталонної та досліджуваної – через один і той же капіляр. В основу методу покладено закон Пуазейля:
де Якщо η1 і η2 – коефіцієнти внутрішнього тертя, відповідно, еталонної та досліджуваної рідини, то
У даному випадку рідина витікає під дією сили тяжіння. Різниця тисків дорівнює гідростатичному тиску ρ g h, де g – прискорення сили тяжіння; ρ – густина рідини; h – висота стовпа рідини. Отже,
Опис установки Слід зауважити, що для вимірювання в’язкостей існує декілька десятків віскозиметрів. Капілярні віскозиметри для абсолютних вимірювань громіздкі, а самі вимірювання складні, тому на практиці їх використовують для відносних вимірювань. Найчастіше використовуваним віскозиметром є прилад Оствальда, який застосовується в даній роботі (рис.5.1).
Віскозиметр Оствальда є U -подібною скляною трубкою, одне коліно якої складається з капілярної трубки С n, кульки Д, та широкої трубки m E.
Прилад розміщують у посудині з водою для забезпечення сталої температури під час експерименту. У кришку посудини вмонтовано термометр T. Лабораторна робота № 20 ВИЗНАЧЕННЯ ПОКАЗНИКА АДІАБАТИ ГАЗІВ γ Мета роботи: експериментально визначити відношення теплоємності газа при постійному тиску Сp до теплоємності газу при постійному об’ємі С v; визначити зміну ентропії ідеального газу при ізохоричному процесі. 1. Обладнання: 1. Скляний балон. 2. Водяний манометр. 3. Насос. Загальні положення Поряд з ізохорним, ізобарним й ізотермічним процесами в термодинаміці часто розглядаються процеси, що протікають під час відсутності теплообміну з навколишніми тілами. Посудини з теплонепроникними стінками називаються адіабатичними оболонками, а процеси розширення або стиску газу в таких посудинах називаються адіабатичними. В адіабатичному процесі Δ Q = 0, тому перший закон термодинаміки приймає вигляд
тобто газ робить роботу за рахунок збутку його внутрішньої енергії. На діаграмі (p, V) процес адіабатичного розширення (або стиску) газу зображується кривою, що називається адіабатою. При адіабатичному розширенні газ здійснює позитивну роботу (A > 0); тому його внутрішня енергія зменшується (Δ U < 0). Це приводить до зниження температури газу. Внаслідок цього тиск газу при адіабатичному розширенні убиває швидше, ніж при ізотермічному. Відношення У даній роботі відношення
Розглянемо суть методу. Скляний балон В, об’єм якого дорівнює декільком літрам, заповнюють повітрям при кімнатній температурі Т1 та атмосферному тиску Р0 (рис. 2.1). Величину тиску можна контролювати за допомогою манометра М, з’єднаного з балоном. За допомогою насоса в балон закачують невелику порцію повітря, що спричиняє збільшення тиску у балоні. Якщо накачку проводити швидко, то за цей час не встигає відбутися теплообмін газу у балоні з навколишнім середовищем. Буде потрібний деякий час (2 – 5 хв.), для того, щоб температура в балоні зрівнялася з температурою навколишнього середовища Т1. При цьому тиск у балоні трохи знизиться:
де h1 – різниця рівнів рідини в манометрі; ρ – густина рідини. Для того, щоб в ході експерименту можна було використовувати рівняння, які описують різні процеси (адіабатичний, ізохоричний, ізотермічний) в газі, розмірковують таким чином. Подумки виділимо в середині балону довільну, достатньо велику порцію повітря, що займає трохи менший об’єм, ніж весь балон з трубками. При незначній зміні загальної кількості повітря при випуску його через кран K кількість повітря у виділеній порції залишається незмінною. У різних процесах газ, що міститься всередині замкнутої поверхні, буде розширюватись і стискатись, виконуючи роботу і обмінюючись теплом з навколишній газом. Оскільки кінетична енергія виникаючого макроскопічного руху мала, ці процеси можна вважати квазістатичними. Графіки процесів зображені на рис. 2.2.
Нехай перший стан виділеної порції газу характеризується параметрами P1, Т1, V1 (див. рис. 2.3, а). Для адіабатичного переходу до другого стану на короткий час відкривають кран Kі випускають незначну кількість повітря (його величина визначається різницею рівнів h1, і перерізом трубки манометра), поки тиск у балоні не зрівняється з атмосферним. Це буде другий стан (див. рис. 2.3, б). Його параметри P2 = P0 , V2 , Т2. Адіабатичне розширення зі зменшенням температури і тиску при переході 1
Потім уже спонтанно, без впливу експериментатора, відбувається теплообмін з навколишнім середовищем доти, поки температура в балоні не стане рівною температурі навколишнього середовища, а тиск не перестане змінюватись і дійде до максимального значення. Це визначиться різницею рівнів рідини в манометрі h2. Таким чином система перейшла в третій стан, який описується такими параметрами (рис. 2.3, г):
При досить великому об’ємі балона і малому перерізі трубки манометра можна знехтувати його об’ємом при переході із стану 2 в стан 3 (V3 = V2) і вважати, що нагрівання приводить тільки до збільшення тиску, а перехід 2→3 є ізохорним. Нижче дамо оцінку такого припущення. Тепер можна перейти до безпосереднього визначення величини γ. Зважаючи на те, що газ в першому і третьому станах має однакову температуру Т1, параметри цих станів запишемо згідно закона Бойля-Маріотта
Враховуючи, що V3 = V2, піднесемо вираз (2.2) в ступінь γ:
З виразу (2.1) виходить
Прирівнюючи праві частини виразів (2.3) і (2.4), одержимо:
а з урахуванням того, що
Перетворимо праву частину виразу (2.5), вважаючи ρ g h1 і ρ g h2 значно меншими, порівняно з P0:
Підставляючи останній вираз в праву частину рівняння (2.5), одержуємо:
або
Зазначимо, що у виразі (2.6) ми знехтували в знаменнику величиною ρgh2 порівняно з P0 і використали розкладення функцій
При малих x можна використовувати лише лінійну частину рівняння. Таким чином, експериментальне визначення γ = Сp / СV, зводиться до вимірювання h1 і h2. Проведемо оцінку наближення V3 = V2 . Оскільки зміна температури, тиску і об’єму повітря дуже мала, для спрощення можна з ними поводитись як з нескінченно малими величинами, тобто диференціальними. З рівняння Менделєєва – Клапейрона виходить:
У випадку переходу 2 Для того, щоб вважати процес переходу 2
Тут hо – різниця рівнів рідини в манометрі, яка була б при атмосферному тиску; V – об’єм повітря в балоні; S – площа перерізу трубки манометра. Як видно з виразу (2.10), наближення буде тим більш вірогідним, чим більша густина рідини (hо при цьому зменшується), менший переріз трубки і чим більший об’єм балону. Так, для h1 = 10 м (для рідини, густина якої близька до густини води) S = 1 см2 = 10–4 м 2, V = 5 л = 5·10–3 м 3
де m – маса повітря в балоні; μ = 0,029 кг/моль – молярна маса повітря,
Зважаючи на малу величину h2 , при обчисленні DS можна зробити такі спрощення. Будемо вважати, що P0 – нормальний атмосферний тиск (P0 = ρ g h0, де h0 = 10,33 м),
Прийнявши це до уваги, одержимо робочу формулу для визначення D S:
де V – об’єм повітря в балоні; V0 = 22,4·10–3 м 3 – об’єм 1 моль газу за нормальних умов. Лабораторна робота 21 Загальні положення Відношення кількості теплоти, отриманої тілом в ізотермічному процесі, до температури тепловіддаючого тіла називається приведеною кількістю теплоти:
Приведена кількість теплоти, отримана тілом в будь-якому круговому процесі, дорівнює нулю:
Тут Т – температура, при якій тіло отримує елементарну кількість тепла Δ Q. Для того, щоб інтеграл з попередньої формули дорівнював нулю, під інтегралом повинен стояти повний диференціал деякої функції (само Δ Q не є повним диференціалом):
Функція S є функцією стану (тобто фізичною величиною, що характеризує стан системи і її зміна при термодинамічних процесах не залежить від виду цих процесів) і називається ентропією. Одним з формулювань другого закону термодинаміки є наступне: ентропія замкненої системи при будь-яких процесах у ній не зменшується. В необоротних процесах ентропія завжди збільшується і тільки в оборотних є константою. Твердження другого закону термодинаміки можна розуміти також з позицій статистики. У молекулярно-кінетичній теорії існує формула Больцмана:
де k – стала Больцмана, Р – термодинамічна ймовірність стану, яка дорівнює числу можливих розподілів частинок за координатами і швидкостями, що відповідають даному термодинамічному стану. З цього визначення витікає, що Р – ціле число, не менше за одиницю. Отже, факт, що ентропія замкненої системи не може зменшуватися, говорить про те, що система може переходити тільки або до станів з такою ж термодинамічною ймовірністю (при оборотних процесах), або з більшою (при необоротних). Лабораторна робота 22 Загальні положення Процес вирівнювання температури системи тіл залежить від їх розмірів, кількості та розподілу температур в усьому об’ємі змішуваних тіл. У реальному нерівноважному процесі швидкість зрівнювання температур тіл, що стикаються, обчислена на одиницю об’єму, залежить від їх теплоємності. Якщо в калориметр, який містить деяку кількість води при фіксованій температурі, занурити тіло, нагріте до більш високої температури, відбудеться теплообмін, по закінченні якого встановиться загальна температура. Якщо ми повторимо дослід з тими ж вихідними даними, зменшивши теплоємність зануреного тіла, то одержимо процес, більш близький до оборотного. Ступінь його оборотності в ізольованій системі можна встановити, визначивши зміну ентропії. В такому процесі для твердого тіла та рідини роботою розширення можна знехтувати, тому cp = c v = c, де с – питома теплоємність тіла. Зміну ентропії при переході з першого стану до другого можна виразити так:
Зважаючи на те, що ентропія системи – є адитивною величиною, для системи тіл
де D S – зміна ентропії системи тіл; D Si – зміна ентропії для одного тіла; n – кількість тіл, що складають систему. Лабораторна робота № 23 Загальні положення. На молекулу, розташовану всередині рідини, діють сили міжмолекулярної взаємодії з боку молекул, які її оточують. В середньому цей вплив скомпенсований, і молекула, знаходячись в полі молекулярних сил, не має будь-якого визначеного напрямку діючої на неї сили. Інша справа, коли молекула розташована біля поверхні рідини. Густина пари і газу над поверхнею набагато менша за густину рідини, і тому вплив з боку молекул газу на молекулу поверхневого шару майже відсутній. Таким чином, на молекулу починає діяти некомпенсована сила, спрямована всередину рідини. Така сила називається силою поверхневого натягу і завжди спрямована по нормалі до поверхні всередину рідини. Наявність цієї сили призводить до появи додаткової потенціальної енергії поверхневого шару. Стану рівноваги відповідає мінімум потенціальної енергії, і тому при відсутності зовнішніх сил рідина приймає форму з мінімальною поверхнею, тобто форму кулі. Коефіцієнт поверхневого натягу рідини α визначається роботою, яку треба здійснити силам поверхневого натягу, щоб утворити поверхню на межі рідини і газу
і вимірюється в Дж/м 2. Також коефіцієнт поверхневого натягу можна визначити як силу, що діє на будь-який елемент лінії поверхні рідини:
Метод відриву кільця Установку для визначення коефіцієнта поверхневого натягу води методом відриву кільця зображено на рис. 3.1 (терези Жолі). Тонкостінне кільце А (виготовлене з матеріалу, що добре змочується досліджуваною рідиною) підвішується на пружині В. Підвіску кільця виконують таким чином, щоб його вісь була вертикальною. Пружина В прикріплена до кронштейна К, жорстко з’єднаного із штангою. Видовження пружини В (і тим самим силу її натягу) можна виміряти за міліметровою шкалою С, якщо заздалегідь про-градуювати пружину.
стінках кільця, а кільце трохи втягнеться всередину рідини. Цей ефект можна помітити при невеликому розтяганні пружини, у момент, коли кільце торкнеться поверхні води. Якщо після цього почнемо повільно опускати посудину з водою, пружина буде поступово розтягуватись, аж поки кільце А не відірветься ві
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.017 с.) |

 (2.1)
(2.1) добуток значень тиску та об’єму газу є сталою величиною
добуток значень тиску та об’єму газу є сталою величиною (2.3)
(2.3) – термічний коефіцієнт об’ємного розширення, який вважається однаковим для всіх ідеальних газів.
– термічний коефіцієнт об’ємного розширення, який вважається однаковим для всіх ідеальних газів. (2.4)
(2.4) – термічний коефіцієнт тиску.
– термічний коефіцієнт тиску.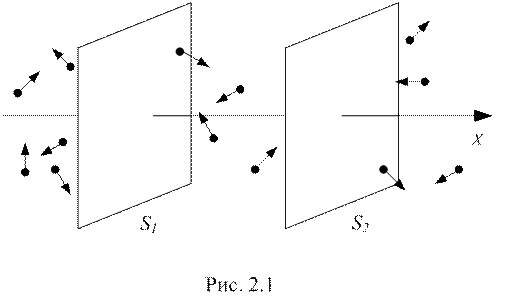
 , а за час Δ t цю відстань пройдуть
, а за час Δ t цю відстань пройдуть  молекул. Тепер можемо обчислити, наскільки більше маси було перенесено в область справа від D S2, ніж в область зліва від D S1:
молекул. Тепер можемо обчислити, наскільки більше маси було перенесено в область справа від D S2, ніж в область зліва від D S1: (2.1)
(2.1) (2.2)
(2.2) ,(2.3)
,(2.3) – середня арифметична швидкість молекул речовини.
– середня арифметична швидкість молекул речовини. ,
, ,(2.4)
,(2.4) ,(2.5)
,(2.5) , а шар В – зі швидкістю
, а шар В – зі швидкістю  . Молекули постійно переходять з одного шару до іншого, в середньому в однаковій кількості. Зміна імпульсу шару А буде такою:
. Молекули постійно переходять з одного шару до іншого, в середньому в однаковій кількості. Зміна імпульсу шару А буде такою: ,
, – маса молекул, що перейшли з одного шару до іншого за час
– маса молекул, що перейшли з одного шару до іншого за час  . Згідно з другим законом Ньютона,
. Згідно з другим законом Ньютона, .
. ,(2.6)
,(2.6) (2.7)
(2.7) ,(2.8)
,(2.8) ,(2.1)
,(2.1) – градієнт швидкості вздовж напрямку z, перпендикулярному до площіни S. У випадку руху газу (рідини) вздовж круглої трубки, замість
– градієнт швидкості вздовж напрямку z, перпендикулярному до площіни S. У випадку руху газу (рідини) вздовж круглої трубки, замість 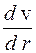 , де r – відстань від осі труби вздовж радіусу.
, де r – відстань від осі труби вздовж радіусу. .(2.1)
.(2.1)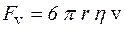 .(2.2)
.(2.2) , виштовхувальна сила
, виштовхувальна сила  , сила опору рухові
, сила опору рухові  (рис. 2.1):
(рис. 2.1):
 ;
; ,
, .(2.3)
.(2.3) ,(2.4)
,(2.4) ,(2.5)
,(2.5) ,(4.1)
,(4.1) – різниця тисків на кінцях капіляру, r, l – його радіус і довжина, V – об’єм рідини, що витік за час τ.
– різниця тисків на кінцях капіляру, r, l – його радіус і довжина, V – об’єм рідини, що витік за час τ. .(4.2)
.(4.2) .(4.3)
.(4.3)
 Риски m і n, що знаходяться вище та нижче порожньої кульки Д, обмежують той об’єм рідини, час витікання якої вимірюється. Друге коліно АВ має знизу розширення В.
Риски m і n, що знаходяться вище та нижче порожньої кульки Д, обмежують той об’єм рідини, час витікання якої вимірюється. Друге коліно АВ має знизу розширення В. ,
,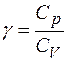 входить в рівняння Пуассона, яке описує стан газу при адіабатичнім процесі, і відіграє важливу роль в реальних технічних процесах, близьких до адіабатичного.
входить в рівняння Пуассона, яке описує стан газу при адіабатичнім процесі, і відіграє важливу роль в реальних технічних процесах, близьких до адіабатичного.
 ,
,
 2 можна описати рівнянням
2 можна описати рівнянням .(2.1)
.(2.1) .
.
 .(2.2)
.(2.2) .(2.3)
.(2.3) .(2.4)
.(2.4) ,
, ,
,  ,
,  , маємо:
, маємо: .(2.5)
.(2.5)
 .(2.6)
.(2.6) ,(2.7)
,(2.7) .(2.8)
.(2.8) в ряд:
в ряд:
 .(2.9)
.(2.9) на
на  , а
, а  на
на  .
. .(2.10)
.(2.10) . Визначимо зміну ентропії при ізохоричному нагріванні повітря в балоні (перехід 2
. Визначимо зміну ентропії при ізохоричному нагріванні повітря в балоні (перехід 2  ,
, , і = 5.
, і = 5. ;
;  .
. ,
, 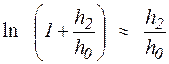 .
. ,(2.11)
,(2.11) .
. .(2.1)
.(2.1) .(2.2)
.(2.2) (2.3)
(2.3) .(2.1)
.(2.1) .(2.2)
.(2.2) (2.1)
(2.1) .(2.2)
.(2.2)
 Підведемо знизу посудину з водою E до кільця, яке нерухомо висить на пружині і піднімемо посудину D, так, щоб кільце трохи доторкнулося поверхні води. При цьому вода почне підніматись по
Підведемо знизу посудину з водою E до кільця, яке нерухомо висить на пружині і піднімемо посудину D, так, щоб кільце трохи доторкнулося поверхні води. При цьому вода почне підніматись по



