

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Загальна ознака подільності Б. Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
Содержание книги
- Теми практичних занять для спеціальності 6.010102 –початкова освіта (2 р.н.).
- Навчальний проект для спеціальності 6.010102 – початкова освіта
- Для особистого контролю за одержанням балів
- Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.
- Операція перетину множин та основні властивості (закони) цієї операції.
- Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.
- Малюнок № 1. 19. Задання декартового добутку множин за допомогою графа.
- Малюнок № 1.20. Граф відповідності.
- Розміщення з повтореннями та без повторень.
- Перестановки з повтореннями та без повторення.
- Поняття як форма мислення, зміст і обсяг поняття та зв'язок між ними.
- Діаграма № 2.1. Відношення часткового збігу між поняттями.
- Поняття предиката, його позначення та область визначення. Поняття кванторів існування та загальності, їх позначення та зв'язок між ними.
- Операція кон'юнкції предикатів.
- Операція еквіваленції предикатів.
- Поняття теореми, її будова. Види теорем (дана, обернена, протилежна, обернена до протилежної, спряжені теореми) та зв'язок між ними.
- Поняття міркування, правильні та неправильні міркування. Перевірка правильності міркувань з допомогою кругів Л.Ейлера.
- Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Аксіоматичне означення додавання цілих невід’ємних чисел в аксіоматичній теорії. Таблиці і закони додавання.
- Порівняння відрізків, дії над відрізками. Натуральне число як результат вимірювання величини. Натуральне число як міра величини. Натуральне число як міра відрізка.
- Означення операцій додавання і віднімання чисел, що розглядаються як міри відрізків. Трактування множення і ділення, які розглядаються як міри відрізків.
- Позиційні та непозиційні системи числення, запис чисел у позиційних і непозиційних системах числення.
- Алгоритми арифметичних операцій над цілими невід’ємними числами у десятковій системі числення.
- Модуль іу. «системи числення. Подільність чисел. ».
- Загальна ознака подільності Б. Паскаля. Ознаки подільності цілих невід’ємних чисел на 2, 3, 4, 5, 9, 25.
- Прості і складені числа. Нескінченність множини простих чисел. Решето Ератосфена.
- Основна теорема арифметики цілих невід’ємних чисел.
- Обчислення нсд і нск способом канонічного розкладу на прості множники та за алгоритмом Евкліда.
- Ознаки подільності на складені числа.
- Відношення порядку на множині невід’ємних раціональних чисел.
- Десяткові дроби, їх порівняння, операції над ними. Перетворення десяткових дробів у звичайні та звичайних у десяткові.
- Додатні раціональні числа як нескінченні періодичні десяткові дроби. Чисті та мішані періодичні дроби та їх перетворення у звичайні.
- Множина раціональних чисел, модуль раціонального числа, операції над раціональними числами. Властивості множини раціональних чисел.
- Відношення порядку на множині дійсних чисел.
- Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу.
- Тотожні перетворення виразів. Тотожності. Виведення основних тотожностей.
- Рівносильні рівняння. Теореми про рівносильність рівнянь.
- Рівняння з двома змінними. Рівняння лінії. Рівняння прямої та їх види.
- Малюнок № 6.1. Графік рівняння кола.
- Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.
- Застосування рівнянь та їх систем до розв’язування текстових задач.
- Системи та сукупності нерівностей з однією змінною та способи їх розв’язування. Нерівності та системи нерівностей з двома змінними, графічний спосіб їх розв’язування.
- Обернена пропорційність, її властивості та графік.
- Основні геометричні побудови циркулем і лінійкою.
- Побудова прямої, яка проходить через дану на ній точку, перпендикулярно до даної прямої.
- Побудова правильних многогранників.
- Правильні многогранники та їх види.
- Модуль 7: «елементи геометрії. Величини. ».
- Виведення формул для знаходження площі паралелограма, трикутника, трапеції. Формули для знаходження площ поверхонь просторових геометричних фігур.
3. У попередньому пункті ми довели теореми про подільність, які не залежать від системи числення. Розглянемо ще одну теорему про подільність, яка не залежить від системи числення і називається ознака Б.Паскаля. Розглянемо ціле невід’ємне число аєZo: 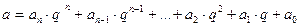 (І) (І)
Теорема (ознака Паскаля): Будь-яке число а, задане в позиційній системі числення з основою q у вигляді (1) ділиться на натуральне число bÎN тоді і тільки тоді, коли на нього ділиться сума добутків цифр цього числа на остачі, утворені при діленні на число b, відповідних степенів основи числення q.
Символічно теорема запишеться так:  (ІІ). У записі (ІІ) (ІІ). У записі (ІІ) 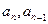 ,…, ,…,  - це цифри числа а. - це цифри числа а. 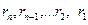 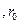 - це остачі від ділення на число b степенів основи системи числення q, тобто чисел - це остачі від ділення на число b степенів основи системи числення q, тобто чисел 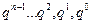 . .
Доведення: Розглянемо ціле невід’ємне число а, яке ділиться на натуральне число в і представлене у вигляді 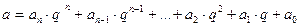 (І). Для доведення теореми нам потрібно довести, що виконується твердження: (І). Для доведення теореми нам потрібно довести, що виконується твердження: 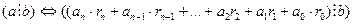 (ІІ), де (ІІ), де  ... ... 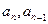 - це цифри числа а, а - це цифри числа а, а 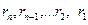 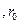 - це остачі від ділення на число b степенів основи системи числення q, тобто чисел - це остачі від ділення на число b степенів основи системи числення q, тобто чисел 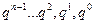 . Оскільки в умові теореми є слова тоді і тільки тоді, то доведення складається із двох частин. У першій частині доведемо необхідну умову: «якщо . Оскільки в умові теореми є слова тоді і тільки тоді, то доведення складається із двох частин. У першій частині доведемо необхідну умову: «якщо 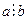 , то сума добутків цифр цього числа на остачі від ділення на число b степенів основи системи числення ділиться націло на b» (див. ІІ), а у другій – достатню умову: «якщо , то сума добутків цифр цього числа на остачі від ділення на число b степенів основи системи числення ділиться націло на b» (див. ІІ), а у другій – достатню умову: «якщо 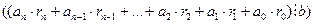 , то , то 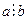 ”. Справедливість цієї теореми приймемо без доведення. ”. Справедливість цієї теореми приймемо без доведення.
У теорії подільності розглядають теореми, які дають можливість з’ясувати питання про подільність на дане число без виконання операцій ділення або шляхом зведення до ділення на значно менші числа. Такі теореми прийнято називати ознаками подільності. Вони залежать від системи числення.
Ознака 1: для того, щоб ціле невід’ємне число a ділилося на 2 необхідно і достатньо, щоб воно закінчувалось парною цифрою.
Доведення: розглянемо aє 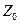 . Представимо його у такому вигляді: . Представимо його у такому вигляді: 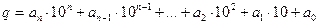 (ІІІ). Щоб використати для доведення теореми ознаку подільності Паскаля, знайдемо остачі від ділення степенів основи числа 10 на число 2. Оскільки (ІІІ). Щоб використати для доведення теореми ознаку подільності Паскаля, знайдемо остачі від ділення степенів основи числа 10 на число 2. Оскільки 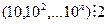 , то , то 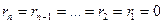 , а тому добутки , а тому добутки 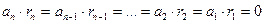 . Отже, число a буде ділитися націло на 2, тоді, коли . Отже, число a буде ділитися націло на 2, тоді, коли 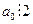 , а це буде тоді, коли , а це буде тоді, коли  або 2, або 4, або 6, або 8. Теорема доведена. або 2, або 4, або 6, або 8. Теорема доведена.
Попередню теорему можна довести і не використовуючи ознаку подільності Б.Паскаля. При цьому доведеться доводити необхідну та достатню умови. Доведемо необхідну умову: „якщо число закінчується парною цифрою, то воно ділиться націло на 2”. За умовою теореми число закінчується парною цифрою, а тому число можна представити у вигляді суми двох доданків так: а=10в+0, а=10с+2, а=10d+4, а=10f+6 і а=10e+8. За теоремами про подільність суми і добутку кожна сума ділиться націло на 2, а тому і число а ділиться націло на 2. Отже, необхідну умову доведено.
Доведемо достатню умову: „якщо число а ділиться націло на два, то воно закінчується парною цифрою”. Представимо число а у вигляді суми а=10b+r. Звідси r=a-10b. Оскільки за умовою a  2, а 10b 2, а 10b  2 ( за теоремою про подільність добутку), то і різниця (a-10b) 2 ( за теоремою про подільність добутку), то і різниця (a-10b)  2, тобто r 2, тобто r  2. r – це одноцифрове число, яке може ділитися націло на 2, якщо воно дорівнює одному з чисел 0, 2, 4, 6, 8. Це означає, що дане число а закінчується парною цифрою. Таким чином, достатню умову доведено. Отже, теорему доведено повністю (пропонуємо студентам довести цим способом самостійно ознаки подільності на 5, на 4 і на 25!). 2. r – це одноцифрове число, яке може ділитися націло на 2, якщо воно дорівнює одному з чисел 0, 2, 4, 6, 8. Це означає, що дане число а закінчується парною цифрою. Таким чином, достатню умову доведено. Отже, теорему доведено повністю (пропонуємо студентам довести цим способом самостійно ознаки подільності на 5, на 4 і на 25!).
Ознака 2: для того, щоб ціле невід’ємне число a ділилося на 5 необхідно і достатньо, щоб воно закінчувалося цифрами 0 або 5.
Ознака 3: для того, щоб ціле невід’ємне число а ділилося націло на 3, необхідно і достатньо, щоб сума цифр цього числа ділилася на 3.
Доведення: використаємо ознаку подільності Паскаля. Представимо число a у вигляді: 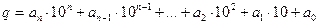 і знайдемо остачі від ділення степенів числа 10 на 3. Маємо: 10:3=3(ост.1), 100:3=33(ост.1), тобто легко бачити, що і знайдемо остачі від ділення степенів числа 10 на 3. Маємо: 10:3=3(ост.1), 100:3=33(ост.1), тобто легко бачити, що 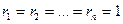 , а тому сума добутків цифр числа a на остачі від ділення на 3 степенів числа 10 перетвориться в суму цифр числа, тобто: , а тому сума добутків цифр числа a на остачі від ділення на 3 степенів числа 10 перетвориться в суму цифр числа, тобто: 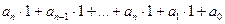 . Якщо ця сума ділиться на 3, то й число поділиться на 3. Теорема доведена. . Якщо ця сума ділиться на 3, то й число поділиться на 3. Теорема доведена.
Ознака 4: для того, щоб ціле невід’ємне число а ділилося націло на 9, необхідно і достатньо, щоб сума цифр цього числа ділилася на 9.
Ознака 5: для того, щоб ціле невід’ємне число а ділилося націло на 4, необхідно і достатньо, щоб число, утворене двома останніми цифрами числа a, ділилося націло на 4.
Доведення: представимо число a у вигляді: 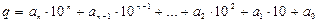 . і знайдемо остачі від ділення степенів числа 10 на 4. Легко бачити, що . і знайдемо остачі від ділення степенів числа 10 на 4. Легко бачити, що 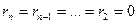 . Тому сума добутків цифр числа a і остач від ділення степенів числа 10 на 4 перетвориться у суму . Тому сума добутків цифр числа a і остач від ділення степенів числа 10 на 4 перетвориться у суму 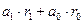 , а це означає, що число a можна представити у вигляді суми двох доданків. Оскільки перший доданок ділиться на 4, то для подільності даного числа a на 4 необхідно і достатньо, щоб виконалась умова , а це означає, що число a можна представити у вигляді суми двох доданків. Оскільки перший доданок ділиться на 4, то для подільності даного числа a на 4 необхідно і достатньо, щоб виконалась умова 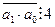 . Таким чином, теорема доведена. . Таким чином, теорема доведена.
Ознака 6: для того, щоб ціле невід’ємне число а ділилося націло на 25, необхідно і достатньо, щоб число, утворене двома останніми цифрами числа a, ділилося націло на 25.
Покажемо застосування доведених ознак до розв’язування прикладів на наступній вправі.
Вправа: з’ясувати, чи ділиться на 2, 3, 4, 5, 9, 25 число 9876501342.
Розв’язання: а) це число ділиться на 2, бо закінчується цифрою 2. Оскільки дане число закінчується цифрою 2, то воно не поділиться на 5.
б) дане число за ознакою подільності ділиться на 3, оскільки сума його цифр (9+8+6+5+7+0+1+3+4+2=45)  3. Оскільки 3. Оскільки 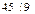 , то дане число також кратне 9. , то дане число також кратне 9.
в) щоб з’ясувати, чи ділиться дане число на 4, утворимо число із двох останніх цифр, тобто число 42. Оскільки 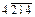 , то дане число не ділиться на 4. Оскільки число, утворене двома останніми цифрами 42 не ділиться націло на 25, то число 9876501342 не ділиться на 25. , то дане число не ділиться на 4. Оскільки число, утворене двома останніми цифрами 42 не ділиться націло на 25, то число 9876501342 не ділиться на 25.
|



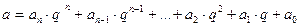 (І)
(І) (ІІ). У записі (ІІ)
(ІІ). У записі (ІІ) 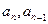 ,…,
,…,  - це цифри числа а.
- це цифри числа а. 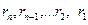
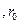 - це остачі від ділення на число b степенів основи системи числення q, тобто чисел
- це остачі від ділення на число b степенів основи системи числення q, тобто чисел 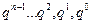 .
.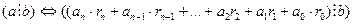 (ІІ), де
(ІІ), де 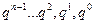 . Оскільки в умові теореми є слова тоді і тільки тоді, то доведення складається із двох частин. У першій частині доведемо необхідну умову: «якщо
. Оскільки в умові теореми є слова тоді і тільки тоді, то доведення складається із двох частин. У першій частині доведемо необхідну умову: «якщо 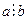 , то сума добутків цифр цього числа на остачі від ділення на число b степенів основи системи числення ділиться націло на b» (див. ІІ), а у другій – достатню умову: «якщо
, то сума добутків цифр цього числа на остачі від ділення на число b степенів основи системи числення ділиться націло на b» (див. ІІ), а у другій – достатню умову: «якщо 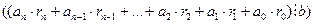 , то
, то 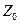 . Представимо його у такому вигляді:
. Представимо його у такому вигляді: 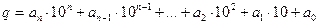 (ІІІ). Щоб використати для доведення теореми ознаку подільності Паскаля, знайдемо остачі від ділення степенів основи числа 10 на число 2. Оскільки
(ІІІ). Щоб використати для доведення теореми ознаку подільності Паскаля, знайдемо остачі від ділення степенів основи числа 10 на число 2. Оскільки 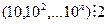 , то
, то 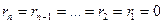 , а тому добутки
, а тому добутки 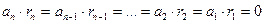 . Отже, число a буде ділитися націло на 2, тоді, коли
. Отже, число a буде ділитися націло на 2, тоді, коли 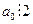 , а це буде тоді, коли
, а це буде тоді, коли  або 2, або 4, або 6, або 8. Теорема доведена.
або 2, або 4, або 6, або 8. Теорема доведена. 2, а 10b
2, а 10b 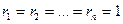 , а тому сума добутків цифр числа a на остачі від ділення на 3 степенів числа 10 перетвориться в суму цифр числа, тобто:
, а тому сума добутків цифр числа a на остачі від ділення на 3 степенів числа 10 перетвориться в суму цифр числа, тобто: 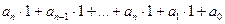 . Якщо ця сума ділиться на 3, то й число поділиться на 3. Теорема доведена.
. Якщо ця сума ділиться на 3, то й число поділиться на 3. Теорема доведена.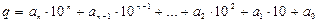 . і знайдемо остачі від ділення степенів числа 10 на 4. Легко бачити, що
. і знайдемо остачі від ділення степенів числа 10 на 4. Легко бачити, що 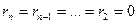 . Тому сума добутків цифр числа a і остач від ділення степенів числа 10 на 4 перетвориться у суму
. Тому сума добутків цифр числа a і остач від ділення степенів числа 10 на 4 перетвориться у суму 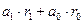 , а це означає, що число a можна представити у вигляді суми двох доданків. Оскільки перший доданок ділиться на 4, то для подільності даного числа a на 4 необхідно і достатньо, щоб виконалась умова
, а це означає, що число a можна представити у вигляді суми двох доданків. Оскільки перший доданок ділиться на 4, то для подільності даного числа a на 4 необхідно і достатньо, щоб виконалась умова 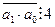 . Таким чином, теорема доведена.
. Таким чином, теорема доведена.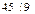 , то дане число також кратне 9.
, то дане число також кратне 9.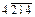 , то дане число не ділиться на 4. Оскільки число, утворене двома останніми цифрами 42 не ділиться націло на 25, то число 9876501342 не ділиться на 25.
, то дане число не ділиться на 4. Оскільки число, утворене двома останніми цифрами 42 не ділиться націло на 25, то число 9876501342 не ділиться на 25.


