
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системи та сукупності рівнянь з двома змінними та способи (алгебраїчні та графічні) їх розв’язування.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
4. Нехай дано два рівняння з двома змінними Означення: системою двох рівнянь з двома невідомими називається кон’юнкція двох рівнянь з двома змінними. Означення: сукупністю двох рівнянь з двома невідомими називається диз’юнкція двох рівнянь з двома змінними. Систему двох рівнянь з двома невідомими, яка складається із рівнянь
f2(х;у)=g2(х;у). (ІІ). Означення: пара чисел Означення: пара чисел Множину всіх таких пар Сукупність рівнянь являє собою диз’юнкцію цих рівнянь, бо сукупність рівнянь буде мати розв’язки тоді, коли існує така пара чисел, що хоча б одне рівняння перетворюються в правильну числову рівність. Саме тому ми сукупність рівнянь записуємо і так: f1(х;у)=g1(х;у)Úf2(х;у)=g2(х;у). Для того, щоб це показати, потрібно довести, що всі розв’язки сукупності перетворюють диз’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення, при яких диз’юнкція предикатів істинна, перетворюють хоча б одне із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел Означення: розв’язати систему рівнянь – це означає знайти множину її розв’язків. Означення: розв’язати сукупність рівнянь – це означає знайти множину її розв’язків. Означення: дві системи рівнянь називаються рівносильними, якщо вони визначені на одній множні та всі розв’язки однієї системи рівнянь є розв’язками другої і навпаки. Означення: дві сукупності рівнянь називаються рівносильними, якщо вони визначені на одній множині та всі розв’язки однієї сукупності рівнянь є розв’язками другої і навпаки. Дві системи чи сукупності рівнянь можуть бути рівносильними в одній числовій області і нерівносильними в іншій. До алгебраїчних методів розв’язування систем рівнянь відносять такі методи: а) метод підстановки. Суть цього методу полягає в тому, що одне із рівнянь системи замінюють рівносильним йому рівнянням, але таким, в якому визначене одне із невідомих, і підставляють у друге рівняння. Внаслідок такої підстановки друге рівняння стає рівнянням з однією змінною. Вправа: розв’язати систему рівнянь: х-2у=3Ù3х-5у=7. Розв’язання. х=2у+3Ù3(2у+3)-5у=7→х=2у+3Ù6у+9-5у=7→х=2у+3Ùу=7-9→х=2у+3Ùу=-2→х=-4+3Ùу=-2→х=-1Ùу=-2. Отже, розв’язком системи рівнянь буде пара чисел (-1;-2). б) метод алгебраїчного додавання. Розв’язуючи систему рівнянь цим методом, деякі її рівняння домножають на спеціально підібрані множники, що визначені при всіх допустимих значення змінних, так, щоб коефіцієнти при одній змінній стали рівними за модулем, а потім почленно додають ці рівняння одне до одного. В результаті таких перетворень одержують рівняння, яке є рівнянням з однієї змінною. Розв’язавши його, знаходять значення цієї змінної, а потім підставляють його в інше рівняння та знаходять значення другої змінної. Вправа: Розв’язати систему рівнянь: 2х-3у=5Ù5х+у=21. Розв’язання. Щоб зрівняти по модулю коефіцієнти при другому невідомому в обох рівняннях, домножимо друге рівняння на 3. Маємо: 2х-3у=5Ù3(5х+у)=63→2х-3у=5Ù15х+3у=63. Додавши до першого рівняння друге, отримаємо рівняння з однією змінною: 17х=68. Отже, х=4. Підставивши це значення у перше рівняння, будемо мати: 8-3у=5→-3у=5-8→-3у=-3→у=1. Таким чином, розв’язком системи рівнянь є пара чисел (4;1). в) метод введення нових невідомих. Під час розв’язування деяких систем буває корисно ввести замість змінних Вправа: розв’язати систему рівнянь: х+у+х/у=9Ù(х+у)●(х/у)=20. Розв’язання. Позначимо х+у=u, x/y=v. Маємо систему u+v=9Ùuv=20, яку можна розв’язати способом підстановки. (9-v)v=20→9v-v²=20→v²-9v+20=0. Розв’язавши це квадратне рівняння, отримаємо два значення v1=4 і v2=5. За цими значеннями знаходимо u1=5 і u2=4. Для знаходження значень х і у потрібно розв’язати такі дві системи: 1) х+у=5Ùх/у=4; 2) х+у=4Ùх/у=5. Із другого рівняння першої системи маємо х=4у, а тому 4у+у=5 і у=1. Тоді х=4. Отже, розв’язком першої системи буде пара чисел (4;1). Із другого рівняння другої системи маємо х=5у, а тому 5у+у=4 і у=2/3. Тоді х=8/3. Отже, розв’язком другої системи є пара чисел (8/3;2/3). Таким чином, дана система рівнянь має розв’язками дві пари чисел (4;1) і (8/3;2/3). Зазначимо, що задача розв’язування системи рівнянь, взагалі кажучи, досить складна і не завжди її можна розв’язати методами елементарної математики. Однак у багатьох випадках шлях розв’язання системи все таки знайти вдається. Для цього доводиться комбінувати різні способи розв’язування систем рівнянь.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.45.223 (0.007 с.) |

 і
і  . Говорять, що вони утворюють систему рівнянь з двома змінними, якщо потрібно знайти всі пари чисел, при підстановці яких в кожне рівняння системи воно перетворюється в правильну числову рівність. Якщо потрібно знайти всі пари чисел, при підстановці яких хоча б в одне рівняння воно перетворюється в правильну числову рівність, то говорять про сукупність двох рівнянь з двома невідомими. Таким чином, приймемо наступні означення.
. Говорять, що вони утворюють систему рівнянь з двома змінними, якщо потрібно знайти всі пари чисел, при підстановці яких в кожне рівняння системи воно перетворюється в правильну числову рівність. Якщо потрібно знайти всі пари чисел, при підстановці яких хоча б в одне рівняння воно перетворюється в правильну числову рівність, то говорять про сукупність двох рівнянь з двома невідомими. Таким чином, приймемо наступні означення.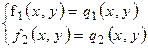 або
або  f1(х;у)=g1(х;у)
f1(х;у)=g1(х;у) , при підстановці яких в кожне рівняння системи замість змінних
, при підстановці яких в кожне рівняння системи замість змінних  і
і  , ми одержуємо правильні числові рівності називається розв’язком системи (І).
, ми одержуємо правильні числові рівності називається розв’язком системи (І). . Для того, щоб це показати, потрібно довести, що всі розв’язки системи перетворюють кон’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення при яких кон’юнкція предикатів істинна, перетворюють кожен із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел
. Для того, щоб це показати, потрібно довести, що всі розв’язки системи перетворюють кон’юнкцію двох предикатів в істинне висловлення, і навпаки, всі значення при яких кон’юнкція предикатів істинна, перетворюють кожен із них в правильне висловлення, тобто в правильну числову рівність. Нехай пара чисел  і
і  замість
замість  .
. і
і 


