
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декомпозиции систем: модели потоков, как модели основания декомпозиции.Содержание книги
Поиск на нашем сайте
Функціонування складних систем пов’язано з деякою подією, тобто з переходом з одного стану в іншій в деякі моменти часу (поняття стану розглядалось в розд. 4). Назвемо потоком подій послідовність однорідних подій, що відбуваються одна за іншою у довільні моменти часу. Потік подій наочно зображується послідовністю крапок на осі часу (рис. 6.5) [3]. Рис. 6.5. Потік подій Нагадаємо, що щільністю (інтенсивністю) потоку називають середню кількість подій в одиницю часу (відповідно до виразу (4.6)). Потік подій називається ординарним, якщо імовірність появи на елементарної дільниці часу Якщо величини Як приклад розглянемо ординарний потік подій без післядії – пуассонівський потік. Якщо події утворюють пуассонівський потік, то кількість подій, що попадають на будь-яку ділянку часу
де а – математичне очікування кількості крапок, що попало на ділянку часу
де Якщо
Відстань Т між двома сусідніми подіями в найпростішому потоці є безперервна випадкова величина, розподілена за показовим законом з щільністю [3, 4]
Для випадкової величини Т, розподіленої за показовим законом
Понятие конфигуратора 30. Понятие конфигуратора Конфигуратор (от англ. формирование)-агрегат состоящий из качественно развитых языков описания си-мы, количество которых минимально, но необходимо для достижения поставленной цели исследуемой си-мы. Агрегирование с помощью конфигуратора подчиняется следующему правилу Анализ си-мы осуществляется на каждом языке конфигуратора отдельно, однако синтез си-мы возможен только при наличии всех языков конфигуратора. Конфигуратор содержит модель высшего уровня, только перечисли все языки на которых говорят о си-ме можно определить ее тип, понять ее природу. Конфигуратор адекватен си-ме. Полноту описания можно достигнуть, дополнив конфигуратор другими языками. Конфигуратор существует в зависимости от целей исследования. При их изменении может потерять свое свойство. Для технических систем конфигуратор является техническим заданием, которое составляется на основе требований нормативно-технической документации, а именно государственный и отраслевой стандарт технических условий и др. документации. В общем случаи техническое задание определяется следующими разделами: 1) Наименование, область применения, основания для разработки 2) Цель и назначения разработки 3) Тактика технических требований к разработки 4) Техн.-економическое требование к разработки 5) Требование к материалам и комплектующим 6) Требования к упаковки, маркировки и т. д. 7) Этапы выполнения работы 8) Порядок контроля и принятия этапов разработки Создаваемая си-ма и все проектные решения должны полностью удовлетворять требования технического задания, соответственно эксплуатационные документы должны полностью соответствовать полученным проектным решениям, в результате формирования си-ма согласовывается с технической документацией, не допускающей множество толкований 31. Агрегати-оператори – це агрегати, щовиконуютьфункціївстановленнявідносинміжелементами, щоагрегуються. До них відносятькласифікатори,оператори-функції та статистики.Одна з розповсюджених ситуацій, що вимагає агрегування, полягає у тому, що сукупність даних, з якими доводиться мати справу, занадто численна і погано доступна для огляду, а для людини характерне прагнення систематизувати великий об'єм даних, щоб «навести порядок» у своєму сприйнятті цієї розмаїтості. Найпоширенішим способом наукової систематизації є класифікація. Класифікація ‑ система супідрядних понять (класів, явищ, об'єктів) у деякій галузі знання, складена з урахуванням загальних ознак об'єктів і закономірностей зв'язків між ними [1, 2].Найпростіший спосіб агрегування складається у встановленні відносин еквівалентності між елементами, тобто в утворенні класів ‑ розподілі досліджуваних об'єктів залежно від їхніх загальних ознак.Підходи до виділення класів моделей можуть бути різними, в загальному випадку якщо представити клас як результат дії агрегату-оператора, то він має наступного вигляду [1]:Одним з найважливішім прикладам агрегування є статистичний аналіз. Статистики – функцій вибіркових значень, що витягають всю корисну інформацію про параметр, що цікавить нас, із сукупності спостережень [1].Статистики використовують наступну важливу властивість [4]:
Це правило справедливо за умови, що вплив на суму окремих доданків повинний бути рівномірно малим, тобто щоб до складу суми не входили члени, що явно переважають за своїм впливом на розсіювання над сукупністю інших. При виконанні цієї умови розглянемо такі правила. Правило 1. При досить великій кількості незалежних досвідів середнє арифметичне спостережених значень випадкової величини сходиться по ймовірності до її математичного очікування. Правило 2. Якщо досліджувана випадкова величина може бути представлена у вигляді суми досить великого числа незалежних (або слабко залежних) елементарних доданків, кожне з яких окремо порівняно мало впливає на суму, то закон розподілу суми стає приблизно нормальним. Це правило називається центральною граничною теоремою. 32. Агрегати-оператори – це агрегати, що виконують функції встановлення відносин між елементами, що агрегуються. До них відносять: класифікатори, оператори-функції та статистики. Одна з розповсюджених ситуацій, що вимагає агрегування, полягає у тому, що сукупність даних, з якими доводиться мати справу, занадто численна і погано доступна для огляду, а для людини характерне прагнення систематизувати великий об'єм даних, щоб «навести порядок» у своєму сприйнятті цієї розмаїтості. Найпоширенішим способом наукової систематизації є класифікація. Класифікація ‑ система супідрядних понять (класів, явищ, об'єктів) у деякій галузі знання, складена з урахуванням загальних ознак об'єктів і закономірностей зв'язків між ними. Найпростіший спосіб агрегування складається у встановленні відносин еквівалентності між елементами, тобто в утворенні класів ‑ розподілі досліджуваних об'єктів залежно від їхніх загальних ознак.Підходи до виділення класів моделей можуть бути різними, в загальному випадку якщо представити клас як результат дії агрегату-оператора, то він має наступного вигляду [1]: ЯКЩО (умови на ознаки, що агрегуються), ТО (ім'я класу). Класифікація є важливим, багатофункціональним і багатобічним явищем у системному аналізі. Однак агрегування у класи – це ефективна, але далеко не тривіальна процедура. Це зумовлено наступними причинами: 1. При наявності ознаки належності до класу на практиці частіше виникає питання надійності та правильності класифікації. 2. Складність класифікації різко зростає, якщо ознака класифікації не спостерігається безпосередньо, а є агрегатом непрямих ознак. Інший тип агрегату-оператора виникає, якщо ознаки, що агрегуються, фіксуються на числових шкалах. Існують такі шкали: 1) абсолютна шкала, результатом вимірювання за якою є число, що виражає кількість елементів у множині. У даній шкалі початок відліку та одиниці виміру незмінні. Із числами, отриманими по такій шкалі, можна здійснювати будь-які арифметичні операції – всі ці дії будуть осмисленими; 2) шкала відносин, у якій початок відліку незмінний, а одиниці виміру можна масштабувати, наприклад, шкали для виміру маси, довжини і т.д.; 3) шкала інтервалів, за якою можна змінювати початок відліку і одиниці виміру, наприклад, шкали для виміру температури (Цельсій, Кельвін, Фаренгейт), тиску, інтервалів часу й т.д.; 4) шкала порядку, при вимірі за якою одержують інформацію про те, у якому порядку об'єкти ідуть один за одним у відповідності до деякої властивості. Прикладом можуть бути шкали, за якими виміряються твердість матеріалів, «подібність» об'єктів. До цієї групи шкал належить більшість шкал, використовуваних у соціологічних і психологічних дослідженнях. Приватним випадком шкал порядку є бальні шкали, використовувані в практиці спортивного суддівства або при зарахуванні абітурієнтів у ВНЗ; 5) шкала найменувань (номінальна), у якій числа використовуються винятково з метою позначення об'єктів. Крім порівняння на збіг, будь-які арифметичні дії над числами, що позначають імена об'єктів, безглузді. За допомогою шкал найменувань часто відзначають, чи є якась ознака в об'єкті. З перерахованих шкал абсолютна шкала є самою «сильною», а шкала найменувань – самою «слабкою». Однак, використовувати тільки абсолютні шкали не завжди доцільно. Для одержання інформації про властивості, вимірювані «сильними» шкалами, потрібно більше досконалі вимірювальні прилади і процедури, у деяких випадках, таких приладів і процедур може просто не бути. 33. якщо агрегат-оператор дає можливість задати відношення на множині ознак у вигляді числової функції багатьох змінних, виражених у деякій шкалі, то його називають агрегатом-функцією. Приватним випадком агрегату-функції є випадок переходу від багатокритеріальної задачі до однокритеріальної за допомогою агрегування декількох критеріїв в один суперкритерій. Багатокритеріальність характеризується наявністю ряду кількісних показників
Різновидом такого суперкрітерію в задачах з різною розмірністю є вираз виду [3]
де Такий підхід має один суттєвий недолік: перехід від багатокритеріальної задачі до однокритеріальної засновано на неявному допущенні, що недолік в одному показнику може бути скомпенсований за рахунок іншого, що, як правило, несправедливо. 34. Агрегат-структура Важливої, а на етапі синтезу – найважливішої, формою агрегування є утворення структур. При синтезі визначають структуру майбутньої системи за допомогою агрегат-структури – моделі системи, що зумовлена потрійною сукупністю: об'єкта, мети і засобів (у тому числі середовища) моделювання. найповнішою моделлює структурна схема, для будови якої слід пройти етапи моделювання за допомогою «чорної шухляди», моделі складу та моделі структури, саме об’єднання цих моделей дозволить синтезувати структурну схему. Тут важливо пам’ятати, що структуру системи слід задавати у всіх її істотних відносинах, тому що в інших відносинах структури зложаться самі стихійним образом (див. підрозд. 2.2). Істотні відносини визначаються конфігуратором системи, тому проект будь-якої системи повинен містити розробку стількох структур, скільки мов включено в її конфігуратор. Підкреслимо, що, хоча структури можуть відрізнятися топологічно, але вони з різних сторін описують ту саму систему, а, отже, зв'язані між собою.Пояснимо випадок агрегування (створення структурної схеми системи) за допомогою агрегату-структури на приклади побудови структури логічних пристроїв.Теоретичною основою побудови найпростіших логічних пристроїв є булева алгебра. Відповідно до стандарту ISO 2382/2-76 кожна залежність, що реалізує ціль (алгоритм) роботи логічного пристрою, має вигляду [6]
де Залежність (7.6) – модель «чорної шухляди» – є булевою функцією, у якої число можливих станів кожної її незалежної змінної дорівнює 2, а її аргументи визначені на множині
В алгебрі логіці використовуються логічні операціїІ, АБО, НЕ – елементи моделі складу –відбивають алгоритми перетворення інформації, представленої у двійковій системі числення(табл. 7.2). Поняття двійкової змінної та логічної операцій утворюють систему аксіом алгебри логіки[7]. Коли елементи системи підібрано, модель «чорного ящика», що реалізується залежністю (7.6), зручно представляти у вигляді таблиці істинності, яка визначає значення вихідної функції залежно від комбінації вхідних сигналів (табл. 7.2) – зв’язки елементів. Таблиця 7.2. Елементи моделі складу та зв’язки у моделі структури
Отже, такій підхід встановлює основні закони формування й перетворення логічних функцій і дозволяє представити будь-яку складну функцію у вигляді композиції найпростіших функцій (рис. 7.1), що найчастіше використається на практиці, тому, що рідко використовуються логічні елементи, які реалізують тільки одну логічну операцію.
При побудові моделі структурної схеми дотримуються наступної послідовності дій [6, 7]: 1. Словесно описується робота схеми – формується конфігуратор системи. 2. Словесний опис формалізується (визначається модель структури) й записується залежно від моделі складу в диз'юнктивній або кон’юнктивній формі по таблицях істинності. 3. Будується структурна схема пристрою. 4. Перевіряється працездатність отриманої моделі (схеми).
35. Процедури системного аналізу: агрегування Агрегування – це протилежна декомпозиції операція, яка здійснює об'єднання (синтез) декількох елементів в єдине ціле. Необхідність агрегування найчастіше зумовлена різними цілями і супроводжується різними обставинами, що приводить до різних способів цієї операції. Однак у всіх агрегатів (лат.: aggregate – приєднувати) – результатів агрегування – відповідно до закону цілісності (див. підрозд. 1.3) є одна загальна властивість – це емерджментність. Агрегування припускає встановлення відносин на заданій множині елементів шляхом використання певних моделей досліджуваної системи. Саме ці моделі жорстко визначають, які частини повинні ввійти до складу системи (наприклад, модель складу) і як вони повинні бути зв'язані між собою (модель структури). Причому різні умови агрегування приводять до використання різних моделей, а, отже, визначають тип остаточного агрегату і техніку його побудови. Визначимо, що для системного аналізу типовими агрегатами є [1]: конфігуратор, агрегат-оператор і агрегат-структура. Агрегат-оператор Агрегати-оператори – це агрегати, що виконують функції встановлення відносин між елементами, що агрегуються. До них відносять [1]:класифікатори,оператори-функції та статистики.Одна з розповсюджених ситуацій, що вимагає агрегування, полягає у тому, що сукупність даних, з якими доводиться мати справу, занадто численна і погано доступна для огляду, а для людини характерне прагнення систематизувати великий об'єм даних, щоб «навести порядок» у своєму сприйнятті цієї розмаїтості. Найпоширенішим способом наукової систематизації є класифікація. Класифікація ‑ система супідрядних понять (класів, явищ, об'єктів) у деякій галузі знання, складена з урахуванням загальних ознак об'єктів і закономірностей зв'язків між ними [1, 2].Найпростіший спосіб агрегування складається у встановленні відносин еквівалентності між елементами, тобто в утворенні класів ‑ розподілі досліджуваних об'єктів залежно від їхніх загальних ознак.Підходи до виділення класів моделей можуть бути різними, в загальному випадку якщо представити клас як результат дії агрегату-оператора, то він має наступного вигляду [1]: ЯКЩО (умови на ознаки, що агрегуються), ТО (ім'я класу). Класифікація є важливим, багатофункціональним і багатобічним явищем у системному аналізі. Однак агрегування у класи – це ефективна, але далеко не тривіальна процедура. Це зумовлено наступними причинами: 1. При наявності ознаки належності до класу на практиці частіше виникає питання надійності та правильності класифікації. 2. Складність класифікації різко зростає, якщо ознака класифікації не спостерігається безпосередньо, а є агрегатом непрямих ознак. Інший тип агрегату-оператора виникає, якщо ознаки, що агрегуються, фіксуються на числових шкалах. Існують такі шкали [2]: 6) абсолютна шкала, результатом вимірювання за якою є число, що виражає кількість елементів у множині. У даній шкалі початок відліку та одиниці виміру незмінні. Із числами, отриманими по такій шкалі, можна здійснювати будь-які арифметичні операції – всі ці дії будуть осмисленими; 7) шкала відносин, у якій початок відліку незмінний, а одиниці виміру можна масштабувати, наприклад, шкали для виміру маси, довжини і т.д.; 8) шкала інтервалів, за якою можна змінювати початок відліку і одиниці виміру, наприклад, шкали для виміру температури (Цельсій, Кельвін, Фаренгейт), тиску, інтервалів часу й т.д.; 9) шкала порядку, при вимірі за якою одержують інформацію про те, у якому порядку об'єкти ідуть один за одним у відповідності до деякої властивості. Прикладом можуть бути шкали, за якими виміряються твердість матеріалів, «подібність» об'єктів. До цієї групи шкал належить більшість шкал, використовуваних у соціологічних і психологічних дослідженнях. Приватним випадком шкал порядку є бальні шкали, використовувані в практиці спортивного суддівства або при зарахуванні абітурієнтів у ВНЗ; 10) шкала найменувань (номінальна), у якій числа використовуються винятково з метою позначення об'єктів. Крім порівняння на збіг, будь-які арифметичні дії над числами, що позначають імена об'єктів, безглузді. За допомогою шкал найменувань часто відзначають, чи є якась ознака в об'єкті. З перерахованих шкал абсолютна шкала є самою «сильною», а шкала найменувань – самою «слабкою». Однак, використовувати тільки абсолютні шкали не завжди доцільно. Для одержання інформації про властивості, вимірювані «сильними» шкалами, потрібно більше досконалі вимірювальні прилади і процедури, у деяких випадках, таких приладів і процедур може просто не бути.Отже, якщо агрегат-оператор дає можливість задати відношення на множині ознак у вигляді числової функції багатьох змінних, виражених у деякій шкалі, то його називають агрегатом-функцією. Приватним випадком агрегату-функції є випадок переходу від багатокритеріальної задачі до однокритеріальної за допомогою агрегування декількох критеріїв в один суперкритерій [1]. Багатокритеріальність характеризується наявністю ряду кількісних показників
Різновидом такого суперкрітерію в задачах з різною розмірністю є вираз виду [3]
Широке розповсюдження даний похід одержав при оцінці рівня якості виготовлення продукції - характеристики якості, що встановлює ступінь відповідності фактичних значень показників якості виготовленої продукції вимогам нормативно-технічних документів.Одним з найважливішім прикладам агрегування є статистичний аналіз. Статистики – функцій вибіркових значень, що витягають всю корисну інформацію про параметр, що цікавить нас, із сукупності спостережень [1]. Статистики використовують наступну важливу властивість [4]:
Це правило справедливо за умови, що вплив на суму окремих доданків повинний бути рівномірно малим, тобто щоб до складу суми не входили члени, що явно переважають за своїм впливом на розсіювання над сукупністю інших. При виконанні цієї умови розглянемо такі правила. Правило 1. При досить великій кількості незалежних досвідів середнє арифметичне спостережених значень випадкової величини сходиться по ймовірності до її математичного очікування. Правило 2. Якщо досліджувана випадкова величина може бути представлена у вигляді суми досить великого числа незалежних (або слабко залежних) елементарних доданків, кожне з яких окремо порівняно мало впливає на суму, то закон розподілу суми стає приблизно нормальним. Це правило називається центральною граничною теоремою.
На практиці застосовується наближена заміна одних законів розподілу іншими: адже, при порівняно малої точності, яка потрібна від імовірнісних розрахунків, така заміна припустима. Вже коли число доданків порядку десяти (а часто й менше) закон розподілу суми звичайно може бути замінений нормальним. Наслідок з правилу 2. Нехай
можна вважати приблизно нормальним. Тоді ймовірність того, що випадкова величина
- втрата корисної інформації, тому що агрегування є неминучим перетворенням (наприклад, по сумі не можна відновити доданків), що в загальному випадку приводить до втрат; - агрегування являє собою вибір певної моделі системи, з яким пов'язані непрості проблеми адекватності; - деяким агрегатам-операторам властива внутрішня суперечливість, сполучена з негативними (стосовно цілям агрегування) наслідкам.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.225 (0.01 с.) |

 двох і більше подій мала в порівнянні з імовірністю появи однієї події. Інтервали
двох і більше подій мала в порівнянні з імовірністю появи однієї події. Інтервали  ординарного потоку можуть бути однаковими й різними, дискретними і безперервними, випадковими і невипадковими. Якщо інтервали невипадкові, то потік подій називається регулярним або детермінованим і повністю характеризується конкретними значеннями
ординарного потоку можуть бути однаковими й різними, дискретними і безперервними, випадковими і невипадковими. Якщо інтервали невипадкові, то потік подій називається регулярним або детермінованим і повністю характеризується конкретними значеннями  .
. є залежними випадковими, то потік називається потоком з післядією, тому що для будь-якого моменту часу наступне значення потоку перебуває в імовірнісній залежності від попередної. Якщо величини
є залежними випадковими, то потік називається потоком з післядією, тому що для будь-якого моменту часу наступне значення потоку перебуває в імовірнісній залежності від попередної. Якщо величини  , розподілена за законом Пуассону:
, розподілена за законом Пуассону: , (6.1)
, (6.1) , (6.2)
, (6.2) – щільність потоку.
– щільність потоку. , пуассонівський потік називають стаціонарним пуассонівським потоком або найпростішим потоком. Для цього потоку кількість подій, що попадають на будь-яку ділянку часу, розподілено по закону Пуассону з параметром
, пуассонівський потік називають стаціонарним пуассонівським потоком або найпростішим потоком. Для цього потоку кількість подій, що попадають на будь-яку ділянку часу, розподілено по закону Пуассону з параметром (6.3)
(6.3)
 ,
,  .
. одні з яких бажано перетворити в максимум, інші – у мінімум. Однак, рішення, що обертає в максимум деякій показник, як правило, інші не обертає ні в максимум ні в мінімум. Тому найчастіше багатокритеріальну задачу зводять до однокритеріальної у такий спосіб:
одні з яких бажано перетворити в максимум, інші – у мінімум. Однак, рішення, що обертає в максимум деякій показник, як правило, інші не обертає ні в максимум ні в мінімум. Тому найчастіше багатокритеріальну задачу зводять до однокритеріальної у такий спосіб: , (
, ( ) (7.1)
) (7.1) ,
,  – мінімальне і максимальне значення
– мінімальне і максимальне значення  -ої характеристики системи;
-ої характеристики системи;  – кількість характеристик системи, необхідних для її дослідження.
– кількість характеристик системи, необхідних для її дослідження. ,
,  (7.6)
(7.6) -
-  -й вхід,
-й вхід,  - число входів,
- число входів,  -
-  -й вихід,
-й вихід,  - число виходів у пристрої.
- число виходів у пристрої. . Отже, кількість можливих функцій Y від x аргументів виражається залежністю:
. Отже, кількість можливих функцій Y від x аргументів виражається залежністю: .
.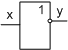 Інверсія – логічне заперечення
(союз НЕ)
Інверсія – логічне заперечення
(союз НЕ)


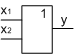 Диз'юнкція - логічне додавання
(союз АБО)
Диз'юнкція - логічне додавання
(союз АБО)



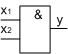 Кон'юнкція - логічне множення
(союз І)
Кон'юнкція - логічне множення
(союз І)

 входить з деякою «вагою»
входить з деякою «вагою»  (
( ), що відбиває його важливість [4]:
), що відбиває його важливість [4]:  ,де
,де  – позитивні для тих критеріїв, значення яких треба збільшити, негативні – для критеріїв, які треба зменшити.
– позитивні для тих критеріїв, значення яких треба збільшити, негативні – для критеріїв, які треба зменшити. – незалежні випадкові величини з математичними очікуваннями
– незалежні випадкові величини з математичними очікуваннями  й дисперсіями
й дисперсіями  . Припустимо, що умови центральної граничної теореми виконуються, число доданків
. Припустимо, що умови центральної граничної теореми виконуються, число доданків  досить для того, щоб закон розподілу величини
досить для того, щоб закон розподілу величини
 попадає в межі ділянки
попадає в межі ділянки  , виражається формулою
, виражається формулою ,де
,де  ,
,  – математичне очікування і середнеквадратичне відхилення величини
– математичне очікування і середнеквадратичне відхилення величини  - нормальна функція розподілу (таблична функція).Відзначимо, що зі створенням агрегату-оператора зв'язаній не тільки виграш, заради якого він створюється, але і деякі ризики [1]:
- нормальна функція розподілу (таблична функція).Відзначимо, що зі створенням агрегату-оператора зв'язаній не тільки виграш, заради якого він створюється, але і деякі ризики [1]:


