
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл засуджених за віком за звітний період (дані умовні)Содержание книги
Поиск на нашем сайте
Розв’язання Частка неповнолітніх злочинців визначається як питома вага кількості злочинців відповідної вікової групи у загальному обсязі вибіркової сукупності, тобто: р = хі / å хі, де хі – кількість неповнолітніх злочинців у вибірці; å хі – загальна кількість злочинців, які потрапили до вибірки. Тоді: р = 14 / 65 = 0,215 і т.д.. Оскільки обсяги генеральної сукупності та вибірки великі, то для визначення граничної помилки використаємо формулу:
де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2; p – частка неповнолітніх злочинців у вибірці; q – частка повнолітніх злочинців у вибірці; n – обсяг вибірки. Оскільки сумарна кількість неповнолітніх та повнолітніх злочинців дорівнює обсягу вибірки, то q = 1 – p, тоді: q = 1 – 0,215 = 0,785. Тоді довірчий інтервал:
Довірчий інтервал записується у вигляді: р = 0,215 Таким чином, з імовірністю 0,954 можна стверджувати, що частка неповнолітніх злочинців становить 0,215, а довірчий інтервал – р = 0,215 Приклад 4 Визначити оптимальний обсяг вибірки для повторного механічного відбору з імовірністю 0,954 за умови, що вік працюючих у генеральній сукупності коливається від 16 до 62 років, а гранична помилка середнього віку працюючих не повинна перевищувати 2 роки. Розв’язання Оптимальний обсяг вибірки для повторного механічного відбору обчислюється за формулою:
де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2;
D – гранична помилка. Оскільки дисперсія генеральної сукупності невідома й відсутні дані щодо аналогічних досліджень, то для визначення дисперсії скористаємося правилом трьох сигм, тобто:
Тоді: Тоді оптимальний обсяг вибірки становитиме: n = 2 2 × 7,7 2 / 2 2 = 60. Оскільки гранична помилка не повинна перевищувати 2 роки, то обсяг вибірки округлюємо у більший бік незалежно від того, яка цифра стоїть після цілого числа.
Таким чином, можна зробити висновок – з імовірністю 0,954 можна стверджувати, що оптимальний обсяг вибірки має бути 60 одиниць. Приклад 5 Визначити оптимальний обсяг вибірки для безповторного механічного відбору для визначення частки якісної продукції з імовірністю 0,954 за умови, що обсяг генеральної сукупності дорівнює 2740 виробів, а гранична помилка якісної продукції не повинна перевищувати 0,2. Розв’язання Оптимальний обсяг вибірки для повторного механічного відбору обчислюється за формулою:
де t – квантиль розподілу береться з таблиць нормального розподілу й для імовірності 0,954 t = 2; N – обсяг генеральної сукупності;
D – гранична помилка. Для частки (альтернативної ознаки), коли відсутня будь-яка інформація про структуру сукупності, вважають, що частка р = 0,5, отже:
Тоді оптимальний обсяг вибірки:
Таким чином, можна зробити висновок – з імовірністю 0,954 можна стверджувати, що за таких умов оптимальний обсяг вибірки має бути 25 одиниць. Бібліографічний список до практичного заняття: [5 – 11, 15 - 20]
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ Основна література: 1. Про інформацію: Закон України №2657-ХІІ від 2.10.1992 р. зі змінами і доповненнями. 2. Про заходи щодо розвитку державної статистики: Указ Президента № 1299/1997 від 22.11.97р. 3. Про внесення змін до Закону України “Про державну статистику“: Закон України від 13.07.2000 № 1922-ІІІ із змінами і доповненнями. 4. Про Державну службу статистики України: Указ Президента України № 396/2011 від 06.04.2011 р. 5. Волошина Н.А. Статистика. Курс лекцій. Електрон. навч. посібн. для студ. денної форми навчання. – Дніпропетровськ: ДДФА, 2011. – 141 с. 6. Єріна А. М. Статистика: підручник / Єріна А. М., Пальян З.О. – К.: КНЕУ, 2010. – 351 с. 7. Єріна А. М., Пальян З.О. Теорія статистики: Практикум. – 5-те вид., стер. - К.: Знання, 2006. – 255 с. – (Вища освіта ХХІ століття). 8. Єріна А.М., Моторин Р.М. Статистика: Навчально-методичний посібник для самостійного вивчення дисципліни. – К.; КНЕУ, 2001. – 448 с. 9. Лугінін О.Є. Статистика: Підручник. - 2-ге вид., переробл. і доповн. - К.: Центр навч. л – ри, 2007. – 606 с. 10. Моторин Р.М., Чекотовський Е.В. Статистика для економістів: Навчальний посібник. - К.: Знання, 2009. – 430 с. + ком пакт-диск.
11. Моторин Р.М., Чекотовський Е.В. Статистика. Збірник індивідуальних завдань з використанням Excel: Навч.-метод. посіб. для самост. вивч. дисц. – К.: КНЕУ, 2005. – 268 с. 12. Нариси з історії статистики України, - К.: Держкомстат, 2001. – 56с. 13. Опря А.Т. Статистика (з програмованою формою контролю знань).Математична статистика. Теорія статистики: Навчальний посібник. – К.: Центр навчальної літератури, 2005. – 472 с. 14. Плошко В.Г., Елисеева И.И. История статистики. - М.: Финансы и статистика, 1990. – 196 с.; 15. Практикум по теории статистики: Учеб. пособие./ Под ред. Р.А.Шмойловой –М: Финансы и статистика, 1999 -416 с. 16. Статистика підприємництва: Навчальний посібник /Під ред. П.Г.Вашківа, В.П. Сторожука, - К.: Слобожанщина, 1999. – 600 с. 17. Статистика: Підручник/С.С. Герасименко та ін. – К.: КНЕУ, 2000. – 468 с. 18. Статистика: теоретичні засади і прикладні аспекти. Навчальний посіб. /Р.В. Фещур, А.Ф. Барвінський, В.П. Кічор.– 2-ге вид., оновлене і доповнене. - Львів: ”Інтелект-Захід”, 2003.- 576с. 19. Теорія статистики: Навч. посіб. / Вашків П.Г., Пастер П.І., Сторожук В.П., Ткач Є.І. – К.: Либідь, 2001. – 320с. 20. Уманець Т.В., Пігарєв Ю.Б. Статистика: Навчальний посібник. - К.: Вікар, 2003. – 623 с. – (Вища освіта ХХІ століття). Додаткова література: 21. Журнал “Статистика України”. 22. Журнал “Регіони України. Економіко-статистичні порівняння”. 23. Збірник наукових праць “Проблеми статистики”. 24. Статистичний щорічник України за 1999 (за 2000, 2001, 2002, 2003, 2004, 2005, 2006) р. Держкомстат України / Під. ред. О.Г.Осауленка, - К.: Техніка, 2000 (2001 і т.д.). -576 с. Internet-ресурси: 25. http://portal.rada.gov.ua 26. http://zakon.rada.gov.ua 27. http://economics.com.ua 28. www.kmu.gov.ua/ 29. www.bank.gov.ua/ 30. www.minfin.gov.ua/ 31. www.me.gov.ua/ 32. www.nbuv.gov.ua/ 33. http://www.ukrstat.gov.ua 34. http://www.dneprstat.gov.ua 35. http://www.adm.dp.ua/ 36. http://www.rada.dp.ua/ 37. http://www.donetskstat.gov.ua/ 38. www.vous.vin.ua 39. www.vous.in.lutsk.ua 40. www.zapstat.zp.ua 41. www.stat.uz.ua 42. www.oblstat.kiev.ua 43. http://stat.if.ukrtel.net/ 44. www.stat.lviv.ua 45. www.oblstat.is.com.ua 46. http://www.stat.nk.ukrpack.net 47. http://www.od.ukrstat.gov.ua/ 48. www.poltavastat.gov.ua 49. http://www.te.ukrstat.gov.ua/ 50. www.sumystat.sumy.ua/ 51. http://www.oblstat.rivne.com/ 52. www.uprstat.kharkov.ukrtel.net/ 53. www.stat.ks.ua 54. http://statbrd.ic.km.ua/ukr/index.htm 55. http://www.ck.ukrstat.gov.ua/ 56. http://www.oblstat.cv.ukrtel.net/ 57. www.chernigivstat.gov.ua 58. http://www.gorstat.kiev.ua 59. www.sevstat.sevinfo.com.ua ДОДАТКИ
Додаток А
Значення χ2 –критерію Пірсона для різних рівнів імовірності Р (істотності α)
Додаток Б
Значення критерію Стьюдента (для рівня істотності 0,10; 0,05; 0,01 )
Додаток В
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.128.70 (0.007 с.) |

 ∆w =
∆w = 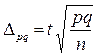 =
= 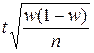 ,
,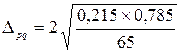 = 0,1.
= 0,1.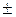 0,1 або 0,115
0,1 або 0,115 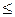 р
р 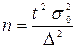 ,
,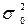 – дисперсія генеральної сукупності;
– дисперсія генеральної сукупності;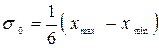 .
.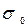 = 1 / 6 (62 – 16) = 7,7.
= 1 / 6 (62 – 16) = 7,7.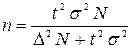 ,
,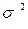 – дисперсія генеральної сукупності;
– дисперсія генеральної сукупності;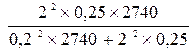 = 25.
= 25.


