
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичні оцінки параметрів розподілуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай з генеральної сукупності Основними властивостями, які повинні мати статистичні оцінки, є властивості незміщеності, ефективності та спроможності. Статистичну оцінку Статистична оцінка При розгляді вибірок великого об’єму статистичні оцінки мають задовольняти умову спроможності . Розрізняють точковіта інтервальні оцінки параметрів розподілу. Точковою називають таку оцінку невідомого параметра, яка визначається одним числом. Інтервальною оцінкою називають таку оцінку, яка визначається двома числами – кінцями інтервалу, відносно якого з наперед заданою точністю можна сказати, що оцінюваний параметр знаходиться всередині заданого інтервалу.
Точкові оцінки математичного сподівання та дисперсії Для побудови точкових оцінок математичного сподівання і дисперсії генеральної сукупності Х (генеральної середньої і генеральної дисперсії) використовують відповідні вибіркові характеристики: вибіркову середню вибіркову дисперсію вибіркове середнє квадратичне відхилення За оцінкугенеральної середньоїприймають вибіркову середню. Ця оцінка буде незміщеною, ефективною та спроможною. Вибіркова дисперсія За оцінкусереднього квадратичного відхиленнягенеральної сукупності приймають виправлене середнє квадратичне відхилення
Така оцінка є зміщеною. На практиці виправленою дисперсією користуються при n <30.
Опитування з теорії 1.Що називається генеральною сукупністю? вибіркою? 2. Що називається варіантами? варіаційним рядом? розмахом вибірки? 3. Що називається частотою, відносною частотою варіант вибірки? 4. Що називаєтьсястатистичним розподілом вибірки? 5. Що являють собою полігон частот, гістограма відносних частот вибірки? 6. Яка функція називається емпіричною функцією розподілу? 7. Що розуміють під статистичною оцінкою параметра розподілу? 8. Яка статистична оцінка називається незміщеною? ефективною? спроможною? 9. Яка статистична оцінка називається точковою? 10. Навести формули для обчислення точкових оцінок математичного сподівання, дисперсії, середнього квадратичного відхилення.
Задача 1. Вибірка задана у вигляді ряду розподілу частот
Знайти розподіл відносних частот. Розв’язання. Знайдемо об’єм вибірки Запишемо статистичний ряд розподілу відносних частот
Перевірка: 0,3+0,4+0,2+0,1=1. Задача 2. Вибірка об’єму
Записати статистичний ряд розподілу частот. Розв’язання. Знайдемо частоти, що відповідають відносним частотам Запишемо статистичний ряд розподілу частот
Задача 3. Вибірка задана у вигляді розподілу частот
Знайти емпіричну функцію розподілу. Розв’язання. Знайдемо об’єм вибірки
Задача 4. Побудувати полігон частот та полігон відносних частот за даним розподілом вибірки.
Розв’язання. Відкладемо на осі абсцис варіанти Тепер побудуємо полігон відносних частот. Для цього відкладемо на осі абсцис варіанти
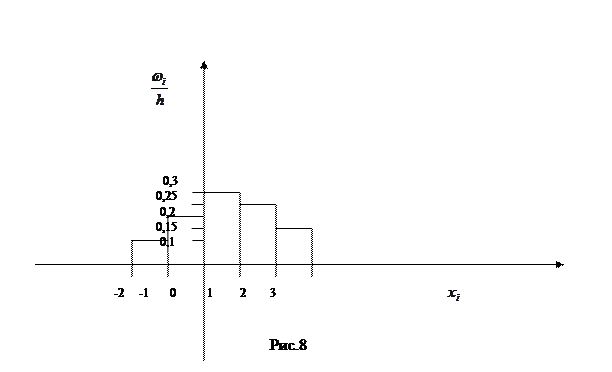
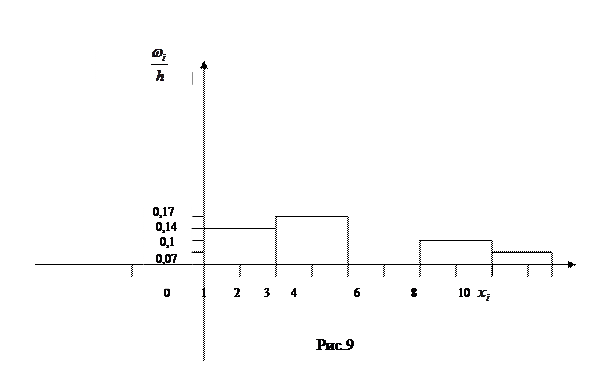
Задача 5. Побудувати гістограму відносних частот інтервального ряду
Розв’язання. Знайдемо об’єм вибірки
Зробимо рисунок гістограми відносних частот
Задача 6. Записати вибірку 0, 2, 8, 3, 6, 0, 0, 8, 7, 3, 2, 0, 3, 6, 2 у вигляді: а) варіаційного ряду; б) статистичного ряду частот і відносних частот. Знайти розмах вибірки. Розв’язання. а) Варіаційний ряд: 0,0,0,0,2,2,2,3,3,6,6,7,8,8. б) Статистичний ряд частот і відносних частот (об’єм вибірки
Розмах вибірки Задача 7. Використовуючи статистичний ряд розподілу, отриманий у попередній задачі, побудувати гістограму відносних частот, розбивши діапазон значень на інтервали довжини Розв’язання. Занесемо дані в таблицю
Для побудови гістограми відкладемо по осі абсцис інтервали довжини
Задача 8. Обчислити незміщені оцінки математичного сподівання та дисперсії вибірки
Розв’язання. Об’єм вибірки
Оскільки Задача 9. В результаті п’яти вимірювань деякої фізичної величини одним приладом отримані такі результати: Розв’язання. а) Знайдемо вибіркову середню б)Знайдемо вибіркову дисперсію Знайдемо виправлену дисперсію в) Знайдемо вибіркове та виправлене середнє квадратичне відхилення:
Задача 10. За вибіркою об’єму Розв’язання. Шукана незміщена оцінка генеральної дисперсії дорівнює виправленій дисперсії Задача 11. Результати вимірювання зросту (в см) випадково відібраних 50 підлітків наведені в таблиці
Знайти вибіркову середню і незміщену вибіркову дисперсію зросту обстежених підлітків, прийнявши за варіанти середини інтервалів. Розв’язання. Запишемо ряд розподілу у вигляді таблиці
Знаходимо вибіркову середню і незміщену вибіркову дисперсію зросту обстежених студентів
Задача 12. Знайти вибіркову середню, вибіркову дисперсію та вибіркове середнє квадратичне відхилення для вибірки, заданої розподілом частот (Вказівка. Перейти до умовних варіант вигляду
Розв’язання. Перейдемо до умовних варіант
Вибіркове середнє квадратичне відхилення
Задачі для аудиторної та самостійної роботи
1. Вибірка задана у вигляді ряду розподілу частот:
Знайти розподіл відносних частот. Відповідь:
2. Вибірка об’єму
Записати статистичний ряд розподілу частот. Відповідь:
3. Вибірка задана у вигляді ряду розподілу частот
Знайти емпіричну функцію розподілу. Відповідь: 4. Побудувати полігон частот та полігон відносних частот за даним розподілом вибірки.
5. Побудувати гістограму відносних частот інтервального ряду
6. Записати вибірку -3, -1, 5, 0, 3, -3, -3, 5, 1, 0, -1, 0, 0, 6, 2 у вигляді: а) варіаційного ряду; б) статистичного ряду частот і відносних частот. Знайти розмах вибірки. Відповідь: а) -3,-3,-3,-1,-1,0,0,0,0,1,2,3,5,5,6;
7. Використовуючи статистичний ряд розподілу, отриманий в попередній задачі, побудувати гістограму відносних частот, розбивши діапазон значень на інтервали довжини 8. Обчислити незміщені оцінки математичного сподівання та дисперсії вибірки
Відповідь: 9. В результаті чотирьох вимірювань температури повітря протягом одного дня отримані такі результати Відповідь: 10. За вибіркою об’єму Відповідь: 11. Результати вимірювання ваги (в кг) випадково відібраних 100 підлітків наведені в таблиці
Знайти вибіркову середню і незміщене середнє квадратичне відхилення ваги обстежених підлітків. (Вказівка. За варіанти взяти середини інтервалів.). Відповідь: 12. Знайти вибіркову середню, вибіркову дисперсію та вибіркове середнє квадратичне відхилення для вибірки, заданої розподілом частот. (Вказівка. Перейти до умовних варіант вигляду
Відповідь: Практичне заняття 10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.166.157 (0.01 с.) |

 з функцією розподілу
з функцією розподілу 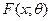 , де
, де  – невідомий параметр, здійснено вибірку (9.1) об’єму п. Задача оцінки невідомого параметра
– невідомий параметр, здійснено вибірку (9.1) об’єму п. Задача оцінки невідомого параметра  , які можна розглядати як оцінку
, які можна розглядати як оцінку 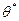 невідомого параметра
невідомого параметра 
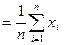 ;
;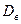
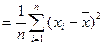 ;
;
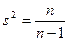
 є незміщеноюоцінкою генеральної дисперсії.
є незміщеноюоцінкою генеральної дисперсії.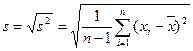 .
.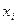

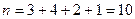 . Знайдемо відносні частоти
. Знайдемо відносні частоти  .
.
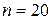 задана у вигляді розподілу відносних частот
задана у вигляді розподілу відносних частот


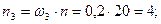


 . За означенням емпірична функція F *(x) дорівнює числу варіант що попадають в інтервал
. За означенням емпірична функція F *(x) дорівнює числу варіант що попадають в інтервал 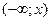 , поділених на об’єм вибірки. Найменша варіанта
, поділених на об’єм вибірки. Найменша варіанта  , тому при
, тому при 
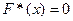 . При
. При  маємо
маємо 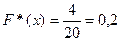 , оскільки значення
, оскільки значення  маємо
маємо  , оскільки варіанта
, оскільки варіанта  з цього інтервалу спостерігалась 8 раз. Якщо
з цього інтервалу спостерігалась 8 раз. Якщо 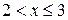 , то варіанта з цього інтервалу значень
, то варіанта з цього інтервалу значень 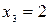 спостерігалась 6 раз. Тому
спостерігалась 6 раз. Тому 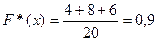 , оскільки ми додаємо частоти варіант з попередніх інтервалів. Для
, оскільки ми додаємо частоти варіант з попередніх інтервалів. Для 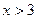 маємо
маємо  , оскільки найбільша варіанта
, оскільки найбільша варіанта 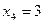 спостерігалась 2 рази. Будуємо графік емпіричної функції розподілу:
спостерігалась 2 рази. Будуємо графік емпіричної функції розподілу:
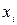 , на осі ординат відносні частоти
, на осі ординат відносні частоти 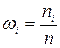 і сполучаємо точки з координатами (
і сполучаємо точки з координатами (

 . Для побудови гістограми частот відкладемо по осі абсцис інтервали довжини
. Для побудови гістограми частот відкладемо по осі абсцис інтервали довжини  . На і -тому інтервалі
. На і -тому інтервалі 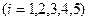 побудуємо прямокутник висоти
побудуємо прямокутник висоти  (щільність відносної частоти). Розрахунки щільності відносних частот зведемо в таблицю:
(щільність відносної частоти). Розрахунки щільності відносних частот зведемо в таблицю: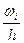

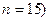
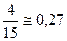



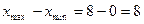 .
.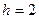 .
.
 . Незміщеною оцінкою математичного сподівання є вибіркова середня
. Незміщеною оцінкою математичного сподівання є вибіркова середня .
.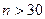 , то виправлена і вибіркова дисперсії мало відрізняються
, то виправлена і вибіркова дисперсії мало відрізняються 
 .
. . Знайти: а) вибіркову середню результатів вимірювань; б) вибіркову і виправлену дисперсії похибок вимірювання; в) вибіркове та виправлене середнє квадратичне відхилення.
. Знайти: а) вибіркову середню результатів вимірювань; б) вибіркову і виправлену дисперсії похибок вимірювання; в) вибіркове та виправлене середнє квадратичне відхилення. .
.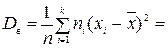
 .
. , використовуючи, що
, використовуючи, що 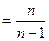
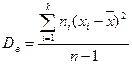 ;
;  .
.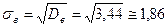 ;
;  .
.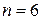 знайдена зміщена оцінка генеральної дисперсії
знайдена зміщена оцінка генеральної дисперсії 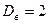 . Знайти незміщену оцінку генеральної дисперсії
. Знайти незміщену оцінку генеральної дисперсії
 .
.
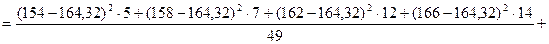
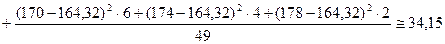 .
. –сталі)).
–сталі)).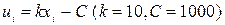 . Складемо таблицю їх розподілу
. Складемо таблицю їх розподілу
 ;
;  ;
;  .
. 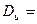
 .
.  ;
; 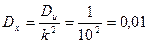 .
.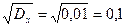 .
. задана у вигляді розподілу відносних частот
задана у вигляді розподілу відносних частот .
. ;
;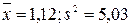 .
.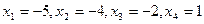 .Знайти: а) вибіркову середню результатів вимірювань; б) вибіркову і виправлену дисперсії спостережуваної температури; в) вибіркове та виправлене середнє квадратичне відхилення.
.Знайти: а) вибіркову середню результатів вимірювань; б) вибіркову і виправлену дисперсії спостережуваної температури; в) вибіркове та виправлене середнє квадратичне відхилення.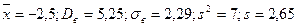 .
. знайдена зміщена оцінка генеральної дисперсії
знайдена зміщена оцінка генеральної дисперсії  . Знайти незміщену оцінку генеральної дисперсії.
. Знайти незміщену оцінку генеральної дисперсії. .
.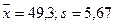 .
. –сталі)).
–сталі)).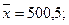
 .
.


