
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні закони розподілу неперервних випадкових величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рівномірний розподіл Неперервна випадкова величина X називається розподіленою рівномірно на відрізку [ a, b ], якщо її щільність розподілу (диференціальна функція розподілу) має вигляд
Рівномірно розподілена на відрізку [ a, b ] випадкова величина X приймає значення тільки з цього проміжку. Інтегральна функція F (x) рівномірного розподілу визначається так:
Якщо проміжок [a, b] єчастиною відрізка [ a, b ]: [a, b]Ì[ a, b ], то ймовірність Р (a £ X £ b) того, що рівномірно розподілена випадкова величина X прийме значення у проміжку [a, b], обчислюється за формулою
Математичне сподівання, дисперсія і середнє квадратичне відхилення випадкової величини X, рівномірно розподіленої на відрізку [ a, b ], обчислюються за формулами
Нормальний закон розподілу Нормальним називається розподіл неперервної випадкової величини X, щільність розподілу якої (диференціальна функція розподілу) має вигляд
де a і s - параметри нормального розподілу (s > 0). Інтегральна функція нормального розподілу має вигляд
де
функція Лапласа. Ймовірність того, що випадкова величина X, розподілена за нормальним законом з параметрами а і s,прийме значення з інтервалу ]a, b[, обчислюється за формулою
Справедлива також формула
за допомогою якої обчислюють ймовірність попадання випадкової величини, розподіленої за нормальним законом, в інтервал, симетричний відносно точки х=а. Математичне сподівання, дисперсія і середнє квадратичне відхилення випадкової величини X, розподіленої за нормальним законом, обчислюються за формулами М (Х) = а, D (Х) = s2, s(Х) = s. (7.9) 8) Для нормального розподілу має місце правило “трьох сигм”: якщо випадкова величина розподілена за нормальним законом, то абсолютна величина її відхилення від математичного сподівання практично не перевищує потроєного середнього квадратичного відхилення 9) P (| X – a | < 3s) = 0,9973» 1. Якщо Х 1, Х 2,..., Хn – однаково розподілені незалежні випадкові величини з математичним сподіванням М (Хi) = a і дисперсією D (Xi) = s2 (i = Показниковий розподіл Неперервна випадкова величина Х називається розподіленою за показниковим (експоненціальним) законом, якщо її щільність розподілу має вигляд
де l = const > 0 – параметр показникового розподілу. Інтегральна функція показникового розподілу має вигляд
Ймовірність того, що випадкова вeличина X прийме значення в інтервалі ]a, b[ (0 < a < b), обчислюється за формулою 10) P (a < X < b) = e –la – e –lb. (7.12) Основні числові характеристики показникового закону розподілу мають вигляд
11) Нехай T - неперервна випадкова величина, що виражає час безвідмовної роботи деякого елемента. В багатьох випадках випадкова величина T розподілена за показниковим законом з інтегральною функцією 12) F (t) = 1 – e –l t (t ³ 0, l = const > 0). 13) Функція R (t) = 1 – F (t) = e –l t (t ³ 0) визначає ймовірність безвідмовної роботи елемента протягом часу t і називається функцією надійності. 14) Параметр l визначає інтенсивність відмов (середнє число відмов елемента за одиницю часу), математичне сподівання випадкової величини T
Опитування з теорії 1. Який вигляд мають диференціальна та інтегральна функції рівномірного розподілу? Побудувати їх графіки. 2. Навести формули для обчислення ймовірності P (a < X < b) та основні числові характеристики випадкової величини, розподіленої рівномірно. 3. Який вигляд мають диференціальна та інтегральна функції нормального розподілу? Побудувати їх графіки. 4. Навести формули для обчислення ймовірностей P (a < X < b), P (| X-a| < e) та основні числові характеристики випадкової величини, розподіленої за нормальним законом. 5. Сформулювати правило “трьох сигм”. 6. Який вигляд мають диференціальна та інтегральна функції показникового розподілу? Побудувати їх графіки. 7. Навести формули для обчислення ймовірності P (a < X < b) та основні числові характеристики випадкової величини, розподіленої за показниковим законом. 8. Який вигляд має функція надійності у випадку показникового закону розподілу часу безвідмовної роботи елемента? Пояснити зміст цієї функції.
Задача 1. Неперервна випадкова величина Х розподілена рівномірно на відрізку [-1; 3]. Записати: 1) щільність розподілу і функцію розподілу Х; 2) обчислити ймовірність потрапляння випадкової величини Х в інтервал ]0,5; 2[; 3) обчислити математичне сподівання, дисперсію і середнє квадратичне відхилення випадкової величини Х. Розв”язання. Для розв”язання задачі використовуємо формули (7.1) – (7.4), поклавши в них а = -1, b = 3. 1) Щільність розподілу f (x) і функція розподілу F (x) випадкової величини Х мають вигляд
2) Ймовірність того, що випадкова величина прийме значення з інтервалу ]0,5; 2[ дорівнює
3) Математичне сподівання, дисперсія і середнє квадратичне відхилення випадкової величини X відповідно дорівнюють
Задача 2. Ціна поділки шкали вимірювального приладу дорівнює 0,1. Дані округлюють до найближчого цілого значення шкали. Вважаючи похибку округлень випадковою величиною, розподіленою рівномірно в інтервалі між двома сусідніми поділками шкали, знайти ймовірність того, що при зніманні показів приладу буде допущена похибка: а) більша за 0,02; б) менша за 0,04. Розв”язання. Нехай випадкова величина Х – похибка округлень. За умовою задачі Х розподілена рівномірно в інтервалі ]0; 0,1[. Функція розподілу випадкової величини Х має вигляд (7.2)
а) Похибка вимірювань перевищить значення 0,02, якщо вона потрапить в інтервал ]0,02; 0,08[. Тоді, за формулою (7.3) маємо
б) Похибка вимірювань буде меншою за 0,04, якщо вона потрапить в один з інтервалів ]0; 0,04[ або ]0,06; 0,1[. Шукану ймовірність Р знаходимо за теоремою додавання ймовірностей несумісних подій Р = Р (0 < X < 0,04) + Р (0,06 < X < 0,1) =
Задача 3. Випадкова величина Х розподілена за нормальним законом і має щільність розподілу
Записати функцію розподілу F (x), знайти математичне сподівання, дисперсію і середнє квадратичне відхилення випадкової величини Х і обчислити ймовірність того, що випадкова величина Х прийме значення: а) з інтервалу ]-1; 3[; б) більше 4; в) менше 1. Розв”язання. Порівнюючи задану щільність розподілу f (x) із загальним виглядом щільності нормального розподілу (7.5), знаходимо параметри нормального закону розподілу а = 2, s =3. У відповідності з формулами (7.6), (7.9) маємо:
М (Х) = а = 2, D (Х) = s2 = 9, s(Х) = s = 3. За формулою (7.7) обчислюємо потрібні ймовірності:
Задача 4. Деталь, виготовлена станком-автоматом, вважається придатною, якщо відхилення Х контрольованого розміру від проектного значення не перевищує 10мм. Точність виготовлення деталей характеризується стандартним відхиленням s. Вважаючи, що для даної технології s = 5 і величина Х розподілена нормально (s(Х) = s, М (Х) = 0), з’ясувати: 1) скільки відсотків придатних деталей виготовляє автомат? 2) якою має бути точність виготовлення, щоб відсоток придатних деталей дорівнював 98? Розв”язання. 1) Деталь, виготовлена станком - автоматом, вважається придатною, якщо виконується умова | X – M (X) | £ 10 або | X | £ 10. За формулою (7.8) знаходимо ймовірність цієї події
Таким чином, станок-автомат виготовляє приблизно 95% придатних деталей. 2) Нову точність s виготовлення деталей, при якій станок- автомат буде виготовляти 98% придатних деталей, знаходимо з умови
Маємо Задача 4.Норма висіву на 1 га дорівнює 160 кг. Випадкові відхилення фактичних витрат насіння на 1га від норми характеризуються середнім квадратичним відхиленням 10 кг. Знайти: а) ймовірність того, що витрати насіння на 100га не перевищать 16,05т; б) кількість насіння, яка забезпечить посів 100 га з імовірністю 0,95. Розв’язання. Нехай Хі = “фактичні витрати насіння для засіву і- го гектара” Розглянемо випадкову величину X = “ витрати насіння для засіву 100га ”. Очевидно, що
Отже, s = s(X) = 100 кг = 0,1т. Тепер обчислюємо потрібну ймовірність Р (Х £ 16,05) = Р (-¥ < Х £ 16,05) = Ф
За таблицею значень функції Ф(х) (Додаток 2) знаходимо значення аргументу для одержаного значення 0,45 функції Лапласа. Воно дорівнює 1,64. Тоді
Ця кількість зерна за даних умов забезпечить засів 100га з ймовірністю 0,95. Задача 6. Випадкова величина Х має показниковий розподіл з функцією розподілу
Записати щільність розподілу f (x), знайти математичне сподівання, дисперсію і середнє квадратичне відхилення випадкової величини Х і обчислити ймовірність того, що в результаті випробування випадкова величина Х прийме значення з інтервалу ] 1; 2[. Розв”язання. Враховуючи загальний вигляд (7.11) функції розподілу F (x) для показникового закону розподілу, знаходимо значення параметра l цього розподілу: l = 3. Далі за формулами (7.10), (7.13) знаходимо щільність розподілу
і основні числові характеристики випадкової величини Х
Ймовірність того, що випадкова величина Х прийме значення з інтервалу ] 1; 2[, обчислюємо за формулою (7.12) P (1 < X < 2) = e –3– e –6 = 0,0498 – 0,00248» 0,047. Задача 7. Випадкова величина Т - час безвідмовної роботи пристрою – розподілена за показниковим законом із щільністю розподілу f (t) = 0,01 e - 0,01 t (t ³ 0 час в годинах). Знайти ймовірність того, що за час t = 50 годин: а) пристрій не відмовить; б) пристрій відмовить. Розв’язання. Параметр l показникового закону розподілу (інтенсивність відмов) дорівнює l = 0,01. а) Ймовірність того, що пристрій пропрацює без відмов протягом t годин знаходимо за допомогою функції надійності R (t) = Р (Т > t) = e –l t = e - 0,01 t (t ³ 0). Отже, R (50) = e –0,01·50 = e –0,5» 0,61. б) Ймовірність відмови пристрою протягом 50 годин знаходимо як імовірність протилежної події Р (Т < t) =1- P (T > t) = 1 – R (t). Отже, Р (Т < 50) = 1 – R (50) = 1 - e –0,5» 0,39.
Задачі для аудиторної і самостійної роботи 1. Неперервна випадкова величина Х розподілена рівномірно на відрізку [ 2; 8]. Записати: а) щільність розподілу і функцію розподілу Х; б) обчислити ймовірність потрапляння випадкової величини Х в інтервал ]1,4; 5[; в) обчислити математичне сподівання, дисперсію і середнє квадратичне відхилення випадкової величини Х. Відповідь: а) б) 0,6. в) M (X) = 5/3; D (X) = 3; s(X) =
2. Автобуси деякого маршруту рухаються строго за графіком з інтервалом руху 5 хв. Знайти ймовірність того, що пасажир, який підійшов до зупинки, буде чекати чергового автобуса: а) менше 3хв; б) більше 2хв. Відповідь: a) 0,6; б) 0,6. 3. Записати диференціальну функцію f (x) випадкової величини Х, розподіленої нормально, якщо М (Х) = 3, D (X) = 16. Відповідь: 4. Математичне сподівання і середнє квадратичне відхилення випадкової величини Х, розподіленої за нормальним законом, відповідно дорівнюють 20 і 5. Знайти ймовірність того, що в результаті досліду Х прийме значення: а) менше12; б) більше 20; в) з інтервалу ]15; 25[. Відповідь: a) 0,0548; б) 0,5; в) 0,6826. 5.Контрольована довжина Х деталі, яка виготовляється станком-автоматом, розподілена за нормальним законом з математичним сподіванням (проектна довжина) 50мм. Фактична довжина виготовлених деталей не менша 32мм і не більша 68мм. Знайти ймовірність того, що довжина навмання взятої деталі: а) більша 55мм; б) менша 40 мм. Відповідь: a) 0,0823; б) 0,0027. 6.Кулька, виготовлена станком-автоматом, вважається придатною, якщо відхилення Х діаметра кульки від проектного розміру менше за абсолютною величиною ніж 0,7 мм. Вважаючи випадкову величину Х розподіленою нормально із середнім квадратичним відхиленням s = 0,4 мм, знайти, скільки придатних кульок буде серед 100 виготовлених. Відповідь: 92. 7. Випадкова величина Х розподілена нормально з математичним сподіванням М (Х) = 10, ймовірність потрапляння Х в інтервал ]10;20[ дорівнює 0,3. Чому дорівнює ймовірність того, що Х потрапить в інтервал ]0;10[? Відповідь: 0,3. 8. Середня вага плодів в одному ящику дорівнює 10кг, а середнє квадратичне відхилення у вазі плодів одного ящика дорівнює 1,5кг. Знайти: а) ймовірність того, що в 100 ящиках буде не менше 970 кг плодів; б) найбільше значення, яке не перевищить вага плодів у 100 ящиках з імовірністю 0,95. Відповідь: 0,9772; б) 1024,7кг. 9. Випадкова величина Х має показниковий розподіл з щільністю розподілу
Записати функцію розподілу F (x), знайти математичне сподівання, дисперсію і середнє квадратичне відхилення випадкової величини Х і обчислити ймовірність того, що в результаті випробування випадкова величина Х прийме значення з інтервалу ] 1; 2[. Відповідь: Р (1< Х <2)» 0,22; M (X) = s(X) = 2,5; D (X) = 6,25. 10.Тривалість часу Т безвідмовної роботи першого з двох незалежно працюючих елементів має показниковий розподіл F 1(t) = 1 – e -0,02 t , другого F 2(t) = 1 – e -0,05 t . Знайти ймовірність того, що за час t = 6 годин: а)обидва елементи відмовлять; б) обидва елементи не відмовлять; в) відмовить тільки один елемент; г) відмовить хоч один елемент. Відповідь: а) 0,03; б) 0,66; в) 0,31; г) 0,34.
Практичне заняття 8
|
||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 2629; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 (7.1)
(7.1)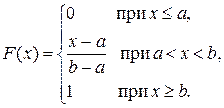 (7.2)
(7.2) . (7.3)
. (7.3) (7.4)
(7.4) , (7.5)
, (7.5) (7.6)
(7.6)
 (7.7)
(7.7) , (7.8)
, (7.8)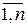 ), то при достатньо великих значеннях n (n >10)розподіл суми Y = X 1 + X 2 + … + Xn близький до нормального з параметрами М (Y) = nа, D (Y) = n s2.
), то при достатньо великих значеннях n (n >10)розподіл суми Y = X 1 + X 2 + … + Xn близький до нормального з параметрами М (Y) = nа, D (Y) = n s2. (7.10)
(7.10) (7.11)
(7.11)

 (7.13)
(7.13)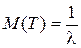 - це середня тривалість безвідмовної роботи елемента.
- це середня тривалість безвідмовної роботи елемента.




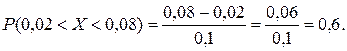

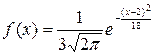 .
.


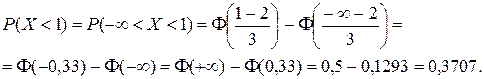


 , звідки, за таблицею значень функції Лапласа, знаходимо
, звідки, за таблицею значень функції Лапласа, знаходимо  або s =
або s = 
 . Для незалежних випадкових величин Хі маємо за умовою M (Xi) = 160 кг, s(Xi) = 10 кг
. Для незалежних випадкових величин Хі маємо за умовою M (Xi) = 160 кг, s(Xi) = 10 кг 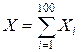 . У відповідності з центральною граничною теоремою вважаємо, що випадкова величина X має нормальний розподіл. Знаходимо параметри цього розподілу.
. У відповідності з центральною граничною теоремою вважаємо, що випадкова величина X має нормальний розподіл. Знаходимо параметри цього розподілу.
 .
. – Ф
– Ф 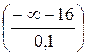 = =Ф(0,5) – Ф(– ¥) = Ф(0,5) + Ф(+ ¥) = 0,1915 + 0,5 = 0,6915.
= =Ф(0,5) – Ф(– ¥) = Ф(0,5) + Ф(+ ¥) = 0,1915 + 0,5 = 0,6915. . Величину
. Величину  або
або  , звідки матимемо
, звідки матимемо ;
; ;
;  .
.
 т.
т.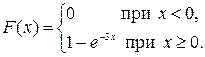

 .
.

 .
. .
.




