
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні задачі мат. СтатистикиСодержание книги Поиск на нашем сайте
А) Розробка методів збору і групування статистичних даних, отриманих в результаті спостережень або ж опрацювання статистичних звітів чи даних у результаті спеціально поставлених експериментів. Б) Розробка методів аналізу статистичних даних залежно від мети досліджень: — оцінка невідомої ймовірності випадкової події на основі спостережень; оцінка невідомої функції розподілу випадкової величини за даними, які отримані в результаті спостережень; оцінка параметрів розподілу, вид якого відомий; оцінка залежності в.в. від однієї або декількох вип. величин. — точність точкового оцінювання, тобто це задача оцінювання близькості між точковою оцінкою параметра та істинним значенням параметра. — перевірка статистичних гіпотез про вид невідомого розподілу або величину параметрів розподілу вид якого невідомий. Поняття генеральної сукупності Генеральна сукупність – це сукупність всіх значень деякої ознаки досліджуваних об’єктів. Що таке вибірка? Вибірковою сукупністю або вибіркою називається сукупність випадково відібраних об’єктів з генеральної сукупності. Об’єм сукупності Об’єм сукупності – це число об’єктів цієї сукупності Основні способи відбору 1) Відбір, що не потребує розподілу генеральної сукупності на частини a. Простий випадковий відбір без повернення b. Простий випадковий повторний відбір 2) Відбір, в якому генеральна сукупність розбивається на частини a. Типовий відбір b. Механічний відбір c. Серійний відбір Простий відбір – це при якому об’єкти вибираються по одному із всієї генеральної сукупності. Типовий відбір – відбір, при якому об’єкти вибираються з кожної типової частини. Механічний відбір – це при якому всю генеральну сукупність ділять на декілька груп і з кожної групи вибирають по одному об’єкту. Серійний відбір – це при якому об’єкти вибираються не по одному, а серіями. Статистичний розподіл вибірки Статистичний розподіл вибірки – це перелік варіант та відповідних їм частот або відносних частот. У випадку, коли обсяг дискретного рядку достатньо великий, то його можна перетворити на інтервальний, тобто статистичний розподіл можна задавати у вигляді послідовності інтервалів та відповідних їм частот (за частоту приймають в даному випадку суму частот елементів вибірки, які попали в даний інтервал). Визначення частоти Число, яке показує скільки разів зустрічалась варіанта хі називається частотою і позначається ni. Визначення відносної частоти Відносна частота показує долю конкретної варіанти у вибірці.
Визначення накопичувальної частоти Накопичувальна частота – це сумарна частота варіант, які розміщені у варіаційному ряді нижче відповідної варіанти (якщо ряд дискретний) або верхнього кінця проміжку (якщо ряд інтервальний). Варіаційний ряд, елемент вибірки Впорядкована за зростанням послідовність Полігони частот та відносних частот Полігон частот – ламана лінія, яка відображає залежність між варіантою та частотою і утворюється шляхом з’єднання прямим лініями точок ( Полігон відносних частот – ламана лінія, яка відображає залежність між варіантою і відносною частотою і утворюється шляхом з’єднання прямими лініями точок Гістограми частот і відносних частот Гістограма частот – це функція, яка має сходинковий характер та складається з прямокутників основами яких є інтервали довжиною h, а висоти дорівнюють відношенню Гістограма відносних частот – це функція, яка має сходинковий характер і складається з прямокутників, основами яких є інтервали довжиною h, а висоти дорівнюють відношенню Основні типи параметрів, що піддаються оцінці Математичне сподівання, дисперсія, функція розподілу, функція щільності
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.209.178 (0.008 с.) |


 називається варіаційним рядом. Елемент
називається варіаційним рядом. Елемент 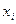 називається і -м членом варіаційного ряду або і -ю варіантою або і -ю впорядкованою статистикою.
називається і -м членом варіаційного ряду або і -ю варіантою або і -ю впорядкованою статистикою. ), де
), де 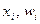 , де
, де  .
. .
.


