
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вибіркові характеристики вибірки, коли дані не повторюютьсяСодержание книги
Поиск на нашем сайте
Вибірковий момент r -го порядку Вибіркове середнє Вибіркова дисперсія Вибіркові характеристики вибірки, коли дані повторюються Вибірковий момент r -го порядку Вибіркове середнє Вибіркова дисперсія
Означення емпіричної функції розподілу Нехай нам відомо статистичний розподіл в.в. Отже, емпіричною функцією розподілу (функцією розподілу вибірки) в.в. Основні властивості емпіричної функції розподілу a. b. c. d. Як визначається функція розподілу, якщо всі компоненти вибірки різні?
Як визначається емпірична функція розподілу, якщо всі компоненти вибірки повторюються?
21. Як визначається мода у випадку, коли дані вибірки повторюються? У випадку коли дані вибірки повторюються мода визначається наступним чином: Складаємо варіаційний ряд і визначаємо варіанту яка найчастіше повторюється. 22. Як визначається медіана у випадку, коли дані вибірки повторюються? Складаємо варіаційний ряд і шукаємо варіанту яка ділить цей ряд пополам. Якщо кількість варіант не парна, то медіаною є елемент Якщо кількість варіант є парною,то медіаною є Як визначаються мода та медіана у випадку, коли дані вибірки згруповані по інтервалах?
h-довжина медіального інтервалу n-об’єм вибірки
24. Статистична оцінка. Статистична оцінка Статистичні оцінки поділяться на:
1. Точкові 2. Інтервальні Точкова оцінка. Точковою оцінкою Основні властивості оцінок. 1.Незміщеність 2. Конзистентність (слушність) 3. Ефективність 27. Незміщеність оцінки. Означає що математичне сподівання оцінки співпадає з самою оцінкою.
Наочно незміщеність оцінки Конзистентність (слушність) оцінки. Часто можна розгляядати не одну оцінку Конзистендність(слушність)- це збіжність оцінки до оцінюваного параметру за ймовірністю при збільшені об’єму вибірки.
Послідовність оцінок
Ефективність оцінки. Ефективність-це властивість незіщеної оцінки мати найменшу дисперсію. Послідовність оцінок
30. Чи є оцінка 31.Чи є оцінка Відповідь для двох: 1.будемо розглядати математичне сподівання. Математичне сподівання будемо оцінювати як середнє арифметичне в результаті випробувань:
В якості оцінки для дисперсії виберемо:
Перевіримо чи є дані оцінки ефективними!
Нехай Чи є незміщенна оцінка матиматичного сподівання, яке визначається як вибіркове середнє:
Доведемо, що в нас є незміщенна оцінка дисперсії
Математичне сподівання не дорівнює оцінці. Дана оцінка дисперсії є зміщеною оцінкою істинною, при великих об’ємах, розходження не суттєве. Для отримання незміщеної оцінки дисперсії, нам потрібно нашу емпіричну дисперсію домножити на
Зазначимо, згідно закону великих чисел при збільшенні n величина збігається за ймовірністю до математичного сподівання.
Щоб довести конзистентність оцінки дисперсії треба виразити дисперсію через 2-ий початковий момент. Другий член збігається за ймовірністю до теоретичного математичного сподівання Якщо математичне сподівання невідомі, то оцінка є незміщеною оцінкою дисперсії.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.25.242 (0.009 с.) |



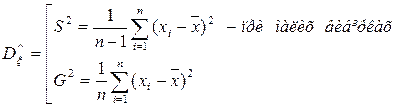



 . Позначимо
. Позначимо  випадкову величину, яка дорівнює кількості елементів вибірки, які менші за х і покладемо
випадкову величину, яка дорівнює кількості елементів вибірки, які менші за х і покладемо  , де дане відношення визначає відносну частоту події, де
, де дане відношення визначає відносну частоту події, де 
 , що визначає відносну частоту події, де
, що визначає відносну частоту події, де 
 - неспадна сходинкова функція
- неспадна сходинкова функція , де
, де  - найменша варіанта
- найменша варіанта , де
, де  - найбільша варіанта
- найбільша варіанта

 (n=2k)
(n=2k)

 - початок медіального інтервалу, тобто це початок такого інтервалу,в якому міститься серединний елемент.
- початок медіального інтервалу, тобто це початок такого інтервалу,в якому міститься серединний елемент. - накопичена проміжку, що передує медіані
- накопичена проміжку, що передує медіані - частота медіанного інтервалу
- частота медіанного інтервалу
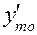 - початок модального інтервалу, тобто такого якому відповідає перша з нагромаджених частот,що перевищує половину всіх спостережень.
- початок модального інтервалу, тобто такого якому відповідає перша з нагромаджених частот,що перевищує половину всіх спостережень. - довжина інтервалу
- довжина інтервалу - частота модального інтервалу.
- частота модального інтервалу. - частота домодального інтервалу
- частота домодального інтервалу - частота післямодального інтервалу
- частота післямодального інтервалу невідомого параметра
невідомого параметра  теоретичного розподілу називається функція
теоретичного розподілу називається функція  від випадкової величини
від випадкової величини  , які отримуються в результаті n спостережень.
, які отримуються в результаті n спостережень. результати n випробувань випадкової величини
результати n випробувань випадкової величини  .
. або
або  .
. можна трактувати наступним чином: при багаторазовому використанні оцінки
можна трактувати наступним чином: при багаторазовому використанні оцінки 
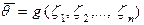 , що побудувона за вибіркою
, що побудувона за вибіркою  , які побудовані також за вибіркою. В цій ситуації природньо говорити про асимптотичну поведінку послідовності оцінок.
, які побудовані також за вибіркою. В цій ситуації природньо говорити про асимптотичну поведінку послідовності оцінок.

 називається сильноконзистендною, якщо вона збігається до оцінюваного параметра з ймовірністю «1», при збільшенні об’єму вибірки.
називається сильноконзистендною, якщо вона збігається до оцінюваного параметра з ймовірністю «1», при збільшенні об’єму вибірки.
 або
або 
 для математичного сподівання незміщеною, консистентною та ефективною?
для математичного сподівання незміщеною, консистентною та ефективною? для дисперсії незміщеною, консистентною та ефективною?
для дисперсії незміщеною, консистентною та ефективною?

 .
.






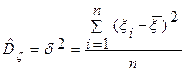


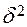 .
.


