
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття математичної статистикиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Поняття математичної статистики Мат. Статистика – це наука, яка вивчає методи збору, класифікації та обробки даних спостереження (статистичних даних) з метою отримання на їх основі обгрунтованих висновків. Мат. Статистика базується на поняттях та методах теорії ймовірностей, причому в деякому розумінні мат. Статистика розв’язує задачі обернені задачам теорії ймовірностей, тобто мат. Статистика виявляє структуру статистичних моделей за результатами проведених спостережень. Основні задачі мат. Статистики А) Розробка методів збору і групування статистичних даних, отриманих в результаті спостережень або ж опрацювання статистичних звітів чи даних у результаті спеціально поставлених експериментів. Б) Розробка методів аналізу статистичних даних залежно від мети досліджень: — оцінка невідомої ймовірності випадкової події на основі спостережень; оцінка невідомої функції розподілу випадкової величини за даними, які отримані в результаті спостережень; оцінка параметрів розподілу, вид якого відомий; оцінка залежності в.в. від однієї або декількох вип. величин. — точність точкового оцінювання, тобто це задача оцінювання близькості між точковою оцінкою параметра та істинним значенням параметра. — перевірка статистичних гіпотез про вид невідомого розподілу або величину параметрів розподілу вид якого невідомий. Поняття генеральної сукупності Генеральна сукупність – це сукупність всіх значень деякої ознаки досліджуваних об’єктів. Що таке вибірка? Вибірковою сукупністю або вибіркою називається сукупність випадково відібраних об’єктів з генеральної сукупності. Об’єм сукупності Об’єм сукупності – це число об’єктів цієї сукупності Основні способи відбору 1) Відбір, що не потребує розподілу генеральної сукупності на частини a. Простий випадковий відбір без повернення b. Простий випадковий повторний відбір 2) Відбір, в якому генеральна сукупність розбивається на частини a. Типовий відбір b. Механічний відбір c. Серійний відбір Простий відбір – це при якому об’єкти вибираються по одному із всієї генеральної сукупності. Типовий відбір – відбір, при якому об’єкти вибираються з кожної типової частини. Механічний відбір – це при якому всю генеральну сукупність ділять на декілька груп і з кожної групи вибирають по одному об’єкту. Серійний відбір – це при якому об’єкти вибираються не по одному, а серіями. Статистичний розподіл вибірки Статистичний розподіл вибірки – це перелік варіант та відповідних їм частот або відносних частот. У випадку, коли обсяг дискретного рядку достатньо великий, то його можна перетворити на інтервальний, тобто статистичний розподіл можна задавати у вигляді послідовності інтервалів та відповідних їм частот (за частоту приймають в даному випадку суму частот елементів вибірки, які попали в даний інтервал). Визначення частоти Число, яке показує скільки разів зустрічалась варіанта хі називається частотою і позначається ni. Визначення відносної частоти Відносна частота показує долю конкретної варіанти у вибірці.
Визначення накопичувальної частоти Накопичувальна частота – це сумарна частота варіант, які розміщені у варіаційному ряді нижче відповідної варіанти (якщо ряд дискретний) або верхнього кінця проміжку (якщо ряд інтервальний). Варіаційний ряд, елемент вибірки Впорядкована за зростанням послідовність Полігони частот та відносних частот Полігон частот – ламана лінія, яка відображає залежність між варіантою та частотою і утворюється шляхом з’єднання прямим лініями точок ( Полігон відносних частот – ламана лінія, яка відображає залежність між варіантою і відносною частотою і утворюється шляхом з’єднання прямими лініями точок Як визначається функція розподілу, якщо всі компоненти вибірки різні?
Точкова оцінка. Точковою оцінкою Основні властивості оцінок. 1.Незміщеність 2. Конзистентність (слушність) 3. Ефективність 27. Незміщеність оцінки. Означає що математичне сподівання оцінки співпадає з самою оцінкою.
Наочно незміщеність оцінки Ефективність оцінки. Ефективність-це властивість незіщеної оцінки мати найменшу дисперсію. Послідовність оцінок
30. Чи є оцінка 31.Чи є оцінка Відповідь для двох: 1.будемо розглядати математичне сподівання. Математичне сподівання будемо оцінювати як середнє арифметичне в результаті випробувань:
В якості оцінки для дисперсії виберемо:
Перевіримо чи є дані оцінки ефективними!
Нехай Чи є незміщенна оцінка матиматичного сподівання, яке визначається як вибіркове середнє:
Доведемо, що в нас є незміщенна оцінка дисперсії
Математичне сподівання не дорівнює оцінці. Дана оцінка дисперсії є зміщеною оцінкою істинною, при великих об’ємах, розходження не суттєве. Для отримання незміщеної оцінки дисперсії, нам потрібно нашу емпіричну дисперсію домножити на
Зазначимо, згідно закону великих чисел при збільшенні n величина збігається за ймовірністю до математичного сподівання.
Щоб довести конзистентність оцінки дисперсії треба виразити дисперсію через 2-ий початковий момент. Другий член збігається за ймовірністю до теоретичного математичного сподівання Якщо математичне сподівання невідомі, то оцінка є незміщеною оцінкою дисперсії.
Гамма-розподіл В.в. має гамма розподіл з параметрами
Де Г-ф-ція визначається як 46. Задається щільністю: n-кількість ступенів свободи n=1,2….
Розподіл Стьюдента В.в.
n-кількість ступені свободи Розподіл Фішера-Снедекора Нехай є дві незалежні в.в
49. Теорема про розподіл Нехай у нас є Відповідно з 50. Теорема про розподіл Нехай у нас є 51 Квантіль розподілу випадкової величини 52. Теорема про розподіл величини Нехай є дві незалежні вип. величини при чому Довірча ймовірність
Довірчий інтервал Інтервал Довірчі границі Інтервал Критерій згоди (означення) Критерії згоди – критерії перевірки гіпотез про розподіл випадкової величини. 90. Критерій Колмогорова, використання критерію Колмогорова, правило перевірки гіпотези Графік лінійної регресії Графік лінійної регресії Вибіркова коваріація 1. Вираз Де
Поняття математичної статистики Мат. Статистика – це наука, яка вивчає методи збору, класифікації та обробки даних спостереження (статистичних даних) з метою отримання на їх основі обгрунтованих висновків. Мат. Статистика базується на поняттях та методах теорії ймовірностей, причому в деякому розумінні мат. Статистика розв’язує задачі обернені задачам теорії ймовірностей, тобто мат. Статистика виявляє структуру статистичних моделей за результатами проведених спостережень.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 954; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.21.106 (0.007 с.) |


 називається варіаційним рядом. Елемент
називається варіаційним рядом. Елемент 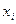 називається і -м членом варіаційного ряду або і -ю варіантою або і -ю впорядкованою статистикою.
називається і -м членом варіаційного ряду або і -ю варіантою або і -ю впорядкованою статистикою. ), де
), де 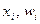 , де
, де 
 називають таку статистичну оцінку,яка визначається одним числом
називають таку статистичну оцінку,яка визначається одним числом  результати n випробувань випадкової величини
результати n випробувань випадкової величини  .
. або
або  .
. можна трактувати наступним чином: при багаторазовому використанні оцінки
можна трактувати наступним чином: при багаторазовому використанні оцінки 
 будемо називати асимптотично незміщеною параметра
будемо називати асимптотично незміщеною параметра  або
або 
 для математичного сподівання незміщеною, консистентною та ефективною?
для математичного сподівання незміщеною, консистентною та ефективною? для дисперсії незміщеною, консистентною та ефективною?
для дисперсії незміщеною, консистентною та ефективною?

 -однаково розподілені, так само як
-однаково розподілені, так само як  .
.






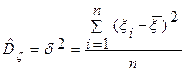


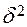 .
. якщо її щільність має вигляд:
якщо її щільність має вигляд:

 розподіл
розподіл
 - квантіль.
- квантіль.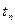 має
має  -розподіл Стьюдента, якщо її щільність задається формулами:
-розподіл Стьюдента, якщо її щільність задається формулами: при
при  .
. , що мають
, що мають  має розподіл Фішера-Снедекора з
має розподіл Фішера-Снедекора з  степенями свободи.
степенями свободи.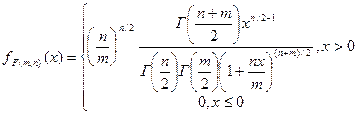
 , де
, де  з
з  ступенями свободи i=
ступенями свободи i= 
 вип. Величин, які є взаємонезалежними та мають
вип. Величин, які є взаємонезалежними та мають  ступенями свободи, тоді
ступенями свободи, тоді  мають
мають  ступенями свободи.
ступенями свободи. (0,1)
(0,1) має
має  , що відповідає ймовірності
, що відповідає ймовірності 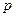 називається таке значення
називається таке значення  , яке випадкова величина не переважає з ймовірності
, яке випадкова величина не переважає з ймовірності  .
.
 де
де 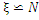 (0,1) η
(0,1) η  розподіл з n ступенем свободи.
розподіл з n ступенем свободи.
 . Величина
. Величина  це як ймовірність того, що випадковий інтервал
це як ймовірність того, що випадковий інтервал  накриває точку
накриває точку  .Ймовірність
.Ймовірність 
 відповідний графік називається графіком лінійної регресії
відповідний графік називається графіком лінійної регресії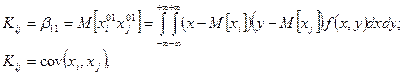
 густина розподілу випадкового вектора
густина розподілу випадкового вектора  . Називається коваріацією двох випадкових величин.
. Називається коваріацією двох випадкових величин.


