
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова довірчих інтервалів для математичного сподівання нормального розподілу при невідомої дисперсії.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо випадкову величину Знайдемо число
Перепишемо вище наведену рівність і отримаємо довірчий інтервал
Зауважимо, якщо n>30 то розподіл Студента прямує до нормального розподілу. 63. Статистична гіпотеза – це деяке твердження(припущення) про вид розподілу випадкової величина, яке потрібно перевірити за даними вибіркової сукупності. 64. Гіпотеза або альтернатива називається простою, якщо їй відповідає лише одне значення параметра Приклад: 65. Гіпотеза або альтернатива називається складною, якщо їй відповідає не одне значення параметра Приклад: 66.Критерій перевірки гіпотези – називають деяку функцію 67. Область прийняття гіпотези – це замкнутий інтервал дійсної осі такий, що при попаданні критерію, що підраховується за даними вибірки, в дану область гіпотеза приймається. Має вигляд 68. Критична область – це інтервал або інтервали дійсної осі такі, що при попаданні критерію, що підраховується за даними вибірки, в дану область гіпотеза не приймається. Складається із тих точок, що не увійшли в область прийняття рішення 69. Помилкою першого роду називають відхилення справедливої гіпотези, тобто ми не приймаємо гіпотезу коли вона є справедливою. 70.Помолкою другого роду називають прийняття гіпотези, коли вона не справджується. 71.Рівнень значущост і – це максимально допустима ймовірність помилок першого роду, позначається 72.Функція потужності критерію
73. За нульову гіпотезу слід приймати те припущення неправильне відхилення якого приводить до менш незначних наслідків. 74. Критичним рівнем значущості називається максимальний рівень значущості при якому гіпотеза приймається. 75. Етапи перевірки статистичних гіпотез: Визначення нульової гіпотеза та альтернатив. Задання рівня значущості. Вибрати критерій перевірки. Визначити критичну область. За результатами експерименту підрахувати фактичне значення критерію. Визначаємо чи належить критерій критичній області, якщо так, то гіпотеза не приймається, інакше приймається. 76. Визначення області прийняття гіпотези та критичну область для гіпотези Виберемо критерій. Оскільки емпіричним аналогом є частота, яка в свою чергу при об’ємі n визначається числом Критерій Із ростом ймовірності p число появи події А, що отримується в результаті спостережень має тенденцію до збільшення. Таким чином велике значення критерію говорить на користь альтернативи. Критична область для гіпотези Ми знаємо, що
Підбираємо мінімальне значення МR=n
Критична область 77. Визначення області прийняття гіпотези та критичну область для гіпотези Виберемо критерій. Оскільки емпіричним аналогом є частота, яка в свою чергу при об’ємі n визначається числом Критерій Із ростом ймовірності p число появи події А, що отримується в результаті спостережень має тенденцію до збільшення. Таким чином велике значення критерію говорить на користь альтернативи. Критична область для гіпотези Ми знаємо, що
Підбираємо мінімальне значення МR=n
Критична область 78. Визначення області прийняття гіпотези та критичну область для гіпотези Критична область Гіпотеза приймається в тому випадку, коли частота появи події А є досить малою і відповідно критична область матиме вигляд
При великих об’ємах використовують нормальний розподіл, при цюму різниця між відкритими і закритими інтервалами стає не суттєвою. Тоді,
Критична область 79. Визначення області прийняття гіпотези та критичну область для гіпотези Гіпотеза відхиляється як при малих значеннях так і при великих, тобі будується область прийняття рішення гіпотези. І визначається як:
Знаємо де МR= Тоді Область прийняття рішень
81. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу 82. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу 83. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу 84. Вибір критерію для перевірки гіпотези про дисперсію Нехай 85. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу 86. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу 87. Визначення області прийняття гіпотези та критичної області при перевірці гіпотези Розглянемо гіпотезу
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 420; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.50.1 (0.009 с.) |

 , що має розподіл Студента із (n-1) степенями свободи.
, що має розподіл Студента із (n-1) степенями свободи. , яке б задовольняло рівність
, яке б задовольняло рівність

 .
. .
. .
.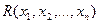 , яка характеризує степінь відповідності вибіркових даних статистичній гіпотезі.
, яка характеризує степінь відповідності вибіркових даних статистичній гіпотезі. .
. .
. . Заданий рівень значущості забезпечується за рахунок вибору критичної області і області прийняття рішень, вибирається таким чином
. Заданий рівень значущості забезпечується за рахунок вибору критичної області і області прийняття рішень, вибирається таким чином  .
. називають ймовірність відхилення основної гіпотези, яка обрахована, що істинне значення параметра
називають ймовірність відхилення основної гіпотези, яка обрахована, що істинне значення параметра 
 - ймовірність підрахування даного параметра
- ймовірність підрахування даного параметра  при альтернативі
при альтернативі 
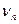 .
. .
. при альтернативі
при альтернативі  визначається наступним чином
визначається наступним чином  . Оскільки в дійсності частота події А не може перевищувати кількість випробувань, критична область визначається
. Оскільки в дійсності частота події А не може перевищувати кількість випробувань, критична область визначається  , необхідно визначити
, необхідно визначити  .
. .Оскільки частота події А може трактуватися як кількість успіхів в n випробуваннях Бернулі з ймовірністю
.Оскільки частота події А може трактуватися як кількість успіхів в n випробуваннях Бернулі з ймовірністю  , то частота підкорюється біноміальному розподілу.
, то частота підкорюється біноміальному розподілу. .
.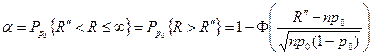
 - функція Лапласа.
- функція Лапласа. - де
- де  квантіль стандартного нормального розподілу.
квантіль стандартного нормального розподілу. .
. при альтернативі
при альтернативі 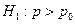 .
. (
( при альтернативі
при альтернативі 
 при якій гіпотеза спростовується.
при якій гіпотеза спростовується. .
. повинно бути найбільше число що задовольняє нерівність:
повинно бути найбільше число що задовольняє нерівність: , звідки визначимо
, звідки визначимо  ;
; .
. при альтернативі
при альтернативі 

 ,
, , DR=
, DR= 
 , звідки визначаємо
, звідки визначаємо  .
. .
. , якщо
, якщо 
 та альтернативу
та альтернативу  .
.  - розподілені за нормальним законом.
- розподілені за нормальним законом.  - верхня
- верхня  - ступенем свободи.
- ступенем свободи.  гіпотеза
гіпотеза  отже область прийняття гіпотези
отже область прийняття гіпотези  .
.
 .
.  гіпотеза
гіпотеза  отже область прийняття гіпотези
отже область прийняття гіпотези  .
.
 .
.  . Отже область прийняття гіпотези
. Отже область прийняття гіпотези  .
. нормального розподілу
нормального розподілу - реалізація вибірки
- реалізація вибірки  , відносно значення дисперсії висувається гіпотеза:
, відносно значення дисперсії висувається гіпотеза:  . В якості критерію візьмемо наступну величину:
. В якості критерію візьмемо наступну величину:  яка має
яка має  - розподіл з
- розподіл з  - вибіркова дисперсія на основі вибірки.
- вибіркова дисперсія на основі вибірки. 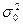 - значення. Яке пропонується.
- значення. Яке пропонується. , якщо
, якщо 
 - фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези:
- фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези: 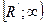 . Критична область:
. Критична область:  . Критерій
. Критерій  має
має  . Область прийняття гіпотези в даному випадку визначається:
. Область прийняття гіпотези в даному випадку визначається:  .
.
 - фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези:
- фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези: 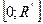 . Тоді
. Тоді  це є квантіль
це є квантіль 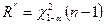 . Область прийняття гіпотези в даному випадку визначається:
. Область прийняття гіпотези в даному випадку визначається:  .
.
 - фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези:
- фіксоване, то більшим значенням істинної дисперсії будуть відповідати більші значення емпіричної дисперсії. Область прийняття гіпотези:  .
.  .
.


