
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема про незміщеність емпіричних початкових моментів.(Доведення)Содержание книги
Поиск на нашем сайте
Емпіричні початкові моменти є незміщеною оцінкою відповідних елементів генеральної сукупності, при умові якщо вони існують.
Для емпіричного початкового моменту n-ого порядку ми маємо:
Нехай в нас є
Доведення аналогічне доведенню нерівності Чебишева.
33. немає
34.Означення кількості інформації за Фішером. Функцію
35.Лема про рівність Якщо майже для всіх
Доведення Використовуючи властивості функції щільності зазначимо:
Візьмемо похідну і маємо:
Введемо наступні позначення:
Маємо:
Візьмемо другу похідну по
Звідси ми отримуємо
Теорему доведено. Теорема про нерівність Крамера-Рао (загальний випадок). Доведення. Нехай задовольняються умови леми про рівність
Причому рівність досягається тоді і тільки тоді,коли Наслідок теореми (про нерівність Крамера-Рао) про ефективність оцінки. Якщо для оцінки
38.Лема про рівність Якщо майже для всіх можливих значень
Доведення аналогічне до леми в питанні 35.
Теорема про нерівність Крамера-Рао (дискретний розподіл). Доведення. Нехай задовольняються умови леми про рівність Тоді виконується нерівність Доведення аналогічне як у питанні 36.
Метод моментів побудови точкових оцінок. Нехай в нас є вибірка Першим загальним методом побудови оцінок невідомих параметрів за вибіркою є метод моментів, що запропонований Пірсоном. Взагалі можна показати, що початковий та центральний емпіричні моменти є конценстендними оцінками відповідно початкового і центрального моментів першого порядку. Згідно з методом моментів певну кількість вибіркових моментів Ці вибіркові моменти обчислюються при значеннях параметрів Перший вибірковий момент:
Розглянемо кількість початкових моментів, що дорівнює кількості невідомих параметрів, які потрібно оцінити, обертають таку саму кількість рівнянь для визначення невідомих параметрів.
Метод максимальної правдоподібності побудови точкових оцінок. Даний метод був запропонований Фішером. Нехай випадкові величини є дискретними. Припустимо,що вид закону розподілу у нас заданий, але невідомий параметр 42. Оцінки максимальної правдоподібності. В якості точкової оцінки
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.103 (0.007 с.) |


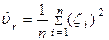

 - незміщена оцінка параметра
- незміщена оцінка параметра  , тоді необхідно і достатньо, що умовою збіжності оцінки
, тоді необхідно і достатньо, що умовою збіжності оцінки 
 називають кількістю інформації за Фішером.
називають кількістю інформації за Фішером.
 - щільність
- щільність . (Доведення загальний випадок)
. (Доведення загальний випадок) існують похідні
існують похідні  , які є мажорвні інтегрованим функціям
, які є мажорвні інтегрованим функціям  і виконується умова
і виконується умова  , то для всіх
, то для всіх 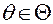
 , а
, а 


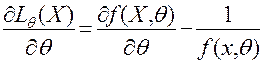


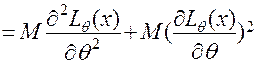
 - незміщена оцінка параметра
- незміщена оцінка параметра  , така що функція
, така що функція  ,
,  ,
,  , тоді виконується нерівність:
, тоді виконується нерівність: , де величина
, де величина  - кількість інформації за Фішером.
- кількість інформації за Фішером. можна подати у вигляді
можна подати у вигляді  .
. виконується нерівність Крамера-Рао, зокрема перетворення на рівність, то оцінка
виконується нерівність Крамера-Рао, зокрема перетворення на рівність, то оцінка  є ефективною.
є ефективною. (для дискретного розподілу). Доведення.
(для дискретного розподілу). Доведення.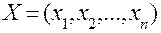 вибірки
вибірки  існують похідні
існують похідні 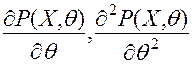 ,
,  ,
,  ,
,  ,
,  ,і
,і  , де
, де
 (для дискретного розподілу) і
(для дискретного розподілу) і  - незміщена оцінка параметра
- незміщена оцінка параметра  збігається абсолютно і рівномірно
збігається абсолютно і рівномірно  , причому рівність справджується тоді і тільки тоді, коли
, причому рівність справджується тоді і тільки тоді, коли 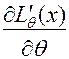 можна подати у вигляді
можна подати у вигляді 
 ,
, 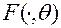 , де розподіл залежить від параметру
, де розподіл залежить від параметру  . Нам потрібно оцінити невідомі параметри
. Нам потрібно оцінити невідомі параметри  .
. прирівнюють до відповідних моментів
прирівнюють до відповідних моментів 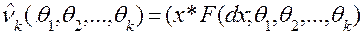 ,розподілу
,розподілу 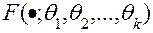 .
. .
.
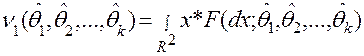



 , потрібно знайти
, потрібно знайти  . Позначимо, що в результаті випробувань величина
. Позначимо, що в результаті випробувань величина  прийме значення:
прийме значення: 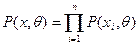 ,
,  - реалізація вибірки. В якості точкової оцінки
- реалізація вибірки. В якості точкової оцінки  при якому функція правдоподібності досягає максимуму, тоді оцінку
при якому функція правдоподібності досягає максимуму, тоді оцінку  - логарифмічна функція правдоподібності. Шукаємо точку мах функції
- логарифмічна функція правдоподібності. Шукаємо точку мах функції  наступним чином: 1)знаходимо похідну:
наступним чином: 1)знаходимо похідну:  ; 2) прирівняємо її до нуля
; 2) прирівняємо її до нуля  і знаходимо корінь даного рівняння, це рівняння правдоподібності; 3) знаходимо другу похідну
і знаходимо корінь даного рівняння, це рівняння правдоподібності; 3) знаходимо другу похідну  , якщо друга похідна від’ємна, то
, якщо друга похідна від’ємна, то  при якому ф-ція правдоподібності досягає максимуму. Тоді оцінку
при якому ф-ція правдоподібності досягає максимуму. Тоді оцінку  наз. оцінкою макс. правдоподібності.
наз. оцінкою макс. правдоподібності.


