
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулювати основні властивості математичного сподівання і дисперсії.Содержание книги
Поиск на нашем сайте
Математичне сподівання постійної величини дорівнює самій постійній М(С) = С. Постійний множник можна виносити за знак математичного сподівання М(СХ)=С*М(Х). Математичне сподівання добутку декількох взаємно незалежних дискретних випадкових величин дорівнює добутку їх математичних сподівань, тобто М(Х1*Х2*…*Хn) = М(Х1)*М(Х2)*…*М(Хn). Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань, тобто М(Х1+Х2+…+Хn) = М(Х1)+М(Х2)+…+М(Хn) Основні властивості дисперсії. 1)Дисперсія будь-якої ДВВ Х невід’ємна
Дійсно, (Х – М(Х))2 невід’ємна, тому згідно означення математичного сподівання та властивостей pk, k =1,2, …, n, D(X) також невід’ємна. 2)Дисперсія постійної величини С дорівнює нулеві D(X) = 0 Дійсно, якщо Х=С, то М(С)= С, тому С – М(С) = 0 3)Постійний множник С можна виносити за знак дисперсії, при цьому постійний множник треба піднести у квадрат D(СX) = С2 D(X). Дійсно, СХ – М(СХ) = С (Х – М(Х)), тому (СХ – М(СХ))2 = С2 (Х – М(Х))2. Постійний множник С2 можна виносити за знак математичного сподівання, тому з формули D(X) = М((Х – М(Х))2) випливає потрібна рівність D(СX) = С2 D(X). 4) Дисперсія ДВВ Х дорівнює різниці між математичним сподіванням квадрата випадкової величини Х та квадрата її математичного сподівання D(X) = М(Х2) – (М(Х))2. Дійсно, D(X) = М((Х – М(Х))2) = М(Х2 – 2ХМ(Х) + М2(Х)) = М(Х2) – 2М2(Х) + М2(Х) = М(Х2) - М2(Х). 5) дисперсія алгебраїчної суми ДВВ Х та Y дорівнює сумі їх дисперсій
2.7.Записати основні закони розподілу д.в.в.: а) біноміальний; б)Пуассона; в)геометричний. Пояснити зміст позначень. Навести приклади д.в.в., розподілених за цими законами. 1. Біноміальний
2.Пуассона
3.Геометричний
4. Гіпергеометричний
Біноміальний закон розподілу. Йм-ті в цьому законі визначаються за формулою P(X=m)=Cmnpm(1-p)n-m, m=0,1,2,…,n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з йм-тю р. Частота настання події А має біноміальний закон розподілу. Числові х-ки закону: MX=np; DX=np(1-p). Випадкова величина X називається розподіленою за законом Пуассона (або, що те саме, має пуассонівський розподіл) з параметром λ, якщо для неї виконується рівність: Пуассонівський розподіл справедливий для подій, які мають малу ймовірність чи трапляються нечасто. Ним, наприклад, можна описати ймовірність того, що футболіст заб'є гол у конкретному матчі. Іноді футболіст забиває один гол, рідше два, ще рідше робить хет-трик, Пеле одного разу забив вісім. Найчастіше футболіст не забиває жодного.
Ймовірність забити k голів за гру визначається параметром λ, що є середньою кількістю голів, які забиває футболіст. Якщо λ велике число, то ймовірність має досягати максимуму при якомусь k. В такому випадку мова йде радше про баскетболіста, який може набирати, наприклад, 22 очка за гру в середньому. Тоді ймовірність набрати 2 очка буде малою. Ймовірність набрати 42 очка теж буде малою, а максимум ймовірності буде в районі саме 22 очок. Геометричний закон розподілу Р(Х=m)=pq, m=1,2,3… Геометр закон розп має частота настання події у схемі незалежних повторних випробувань, якщо вони проводяться до першого настання події. У ф-лі: р– йм-сть настання події в кожному випробу-ванні. Геометричний закон розподілу застосовуєть-ся у задачах статистичного контролю якості і теорії надійності. Числові х-ки: MX=1/p; DX=(1-p)/p2. 2.8.Записати основні закони розподілу н.в.в.: а) рівномірний; б) показниковий; в) нормальний. Пояснити зміст позначень. Навести приклади д.в.в., розподілених за цими законами. 1.Рівномірний. Величина Х розподілена рівномірно у проміжку (a,b), якщо усі її можливі значення належать цьому проміжку і щільність її імовірностей у цьому проміжку постійна, тобто
При х
При х Величина Імовірність влучення Х в інтервал (х1, х2) дорівнює відношенню довжини цього інтервалу до довжини усього проміжку (a,b). Цей розподіл задовольняють, наприклад, похибки округлення різноманітних розрахунків. 2. Нормальний. Випадкову величину Х називають розподіленою нормально, якщо щільність її імовірностей має вигляд
Графік цієї функції називається нормальною кривою або кривою Гаусса. При а=0 та Ϭ=1 нормальну криву називають нормованою а)Ймовірність того, що Х прийме значення, яке належить інтервалу (α,β):
3. Показниковий. Випадкову величину Х називають розподіленою за показниковим законом, якщо щільність її імовірностей має вигляд
при х<0, де λ>0 – параметр. Показниковому розподілу задовольняють: час телефонної розмови, чс ремонту техніки, час безвідмовної роботи комп’ютера. Якщо НВВ Х розподілена за показниковим законом, то вона має математичне сподівання та середнє квадратичне відхилення рівні. Показниковим (експоненціальним) назив розподіл ймовірностей неперервної випадкової величини Х, яка описується функцією щільності Властивості ф-ції розподілу:1) Властивості ф-ції щільності розподілу: 1)
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.73.53 (0.01 с.) |


 .
.

 .
.
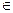 (a,b),
(a,b),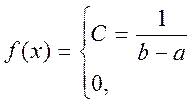
 (a,b).
(a,b). визначається умовою нормування Р(а< X<b) = C(a - b) = 1
визначається умовою нормування Р(а< X<b) = C(a - b) = 1 , де а та σ – параметри розподілу.
, де а та σ – параметри розподілу. Тобто це функція Лапласа яка табульована. Заміна змінної
Тобто це функція Лапласа яка табульована. Заміна змінної 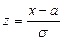 з використанням інтеграла Пуассона.
з використанням інтеграла Пуассона. 

 -функція Лапласа.
-функція Лапласа. 
 при х
при х  0;
0; , λ – постійна додатня величина. Функція розподілу показникового закону
, λ – постійна додатня величина. Функція розподілу показникового закону  Ймовірність попадання в інтервал (а, в):
Ймовірність попадання в інтервал (а, в): 
 ; 2)
; 2) 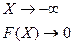 ; 3)
; 3)  ; 4) Ф-ція розподілу F(X) є неспадною ф-цією
; 4) Ф-ція розподілу F(X) є неспадною ф-цією  ; 5)
; 5) 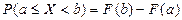
 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 



