
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Записати формули для обчислення математичного сподівання тта дисперсії функцій д.в.в. та н.в.в.Навести приклади.Содержание книги
Поиск на нашем сайте
Мат. сподівання ДВВ Х наз. число, яке = сумі добутків усіх можливих значень Х на відповідні їм імовірності. М(Х)= М(Х)= Дисперсією ДВВ Х наз. число, яке = мат. сподіванню квадрата відхилення ДВВ Х від її мат. сподівання. D(X) = M((X- M(X)) D(X) = f (x; y) = Нехай випадкова дискретна величина Х приймає значення х1, х2,…Xn з відповідними ймовірностями р1,р2,…Pn. Задати закон розподілу такої ВВ- це задати рівність Pk=P(X= Існують 1.Біноміальний ЗР 2.Пуассона 3.Геометричний 4.Гіпергеометричний 5.Поліноміальний
2.26. Пояснити, як будуються випадкові величини, що мають розподіл:а) Пірсона Х2;б) Стьюдента;в) Фішера Розподіл Пірсона (х
Розподіл Стьюдента (t) Нехай Z –нормальна ВВ, M(Z)=0, Має розподіл, який наз. t-розподілом з k ступенями вільності. Розподіл Фішера (F) Якщо U і V- НВВ, розподілені по закону F=(U/k1)/(V/k2)Має розподіл, який наз. розподілом F Фішера. Щильність цього розподілу:
f(x)=
Сформулювати предмет математичної статистикита її основні задачі. Основні задачі: розробка методів збору статистичних даних та їх групування оцінка невідомих параметрів сукупності за даними вибору розробка методів виявлення наявності, виду, щильності, взаємозв’язків між ознаками перевірка статистичних гіпотез.
3.2.Дати означення:а) генеральної та вибіркової сукупностей;б)обсягу вибірки;в) повторної і без повторної, репрезентативної вибірки Генеральна – сукупність об’єктів, з яких зроблено вибірку. Вибіркова – сукупність випадково взятих об’єктів. Об’ємом сукупності наз. кількість об’єктів цієї сукупності. Повторною наз. Вибірку, при якій відібраний об’єкт повертається до генеральної сукупності перед відбором іншого об’єкту. Вибірку наз. безповторною, якщо взятий об’єкт до генеральної сукупності не повертається. Найчастіше використовують без повторні вибірки. Репрезентативна – вибірка, яка здійснюється випадково. Це вибірка яку можна ефективно використовувати для вивчення відповідної ознаки генеральної сукупності. Дати означення статистичної (емпіричної) ф-ї розподілу та сформулювати її основні властивості. Навести приклади побудови емпіричної функції розподілу та її графіки. Емпірична функція розподілу вибірки - це така функція F*(х), значення якої для кожного числа х = відносній частоті події {X<x}.
Дати означення кумулятивних частоти та відносної частоти.Пояснити їх статистичний зміст. Полігоном частот наз. ламану, відрізки якої з’єднують точки (x1, N1), (x2, n2), …, (xm, nm)Полігоном выдносних частот (частостей) наз. ламану, відрізки якої проходять черезточки (x1, w1), (x2, w2), …, (xm, wm). Полігони частот та частостей є аналогами щільності імовірностей. Гістограмою частот називають ступінчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали варіант довжиною h= xk – xk-1, а висоти дорівнюють
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.73.150 (0.006 с.) |

 для ДВВ
для ДВВ для НВВ
для НВВ ) для ДВВ
) для ДВВ
 (
( F(x; y))/(
F(x; y))/( x *
x *  y)- функція щільності СНВВ.
y)- функція щільності СНВВ. ), яку можна розглядати як функцію.
), яку можна розглядати як функцію. )
)
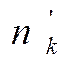 - теоретичні частоти
- теоретичні частоти - спостережене значення критерія
- спостережене значення критерія 
 (Z)=1, а V- незалежна від Z величина, яка розподілена по закону
(Z)=1, а V- незалежна від Z величина, яка розподілена по закону  ступенями вільності. Тоді величина:Т=Z/(V/k)
ступенями вільності. Тоді величина:Т=Z/(V/k) зі степенями вільності К1 і К2.К1- число степенів вільності більшої дисперсії.К2- число степенів вільності меншої дисперсії
зі степенями вільності К1 і К2.К1- число степенів вільності більшої дисперсії.К2- число степенів вільності меншої дисперсії якщо x>0
якщо x>0 , де nx – кількість варіант, які менші від х, n – об’єм вибірки.
, де nx – кількість варіант, які менші від х, n – об’єм вибірки. . тобто F*(х)=
. тобто F*(х)=  Властивості: 1. 0<= F*(х)<=1; 2. F*(х) – зростаюча функція; 3. F*(х)=0 при x<=x1 i F*(х)=1 при x>xm де х1 – наіменша варіанта, xm – найбільша варіанта.
Властивості: 1. 0<= F*(х)<=1; 2. F*(х) – зростаюча функція; 3. F*(х)=0 при x<=x1 i F*(х)=1 при x>xm де х1 – наіменша варіанта, xm – найбільша варіанта. (щільність частоти).Гістограмою відносних частот (частостей) називають ступінчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали варіант, а висоти дорівнюють відношенню
(щільність частоти).Гістограмою відносних частот (частостей) називають ступінчасту фігуру, яка складається з прямокутників, основами яких є часткові інтервали варіант, а висоти дорівнюють відношенню  (щільність частості).Площа гістограми частот дорівнює об'єму вибірки, а площа гістограми частостєй - одиниці.Для накопиченої частоти і накопиченої відносної частоти можуть бути побудовані графіки схожі на полігон частот. Ці графіки називаються полігоном накопиченої частоти або полігоном накопиченої відносної частоти. У статистиці також їх називають огівою або кумулятивною кривою. Полігон накопиченої частоти зручно використовувати у цілому ряді задач статистики.
(щільність частості).Площа гістограми частот дорівнює об'єму вибірки, а площа гістограми частостєй - одиниці.Для накопиченої частоти і накопиченої відносної частоти можуть бути побудовані графіки схожі на полігон частот. Ці графіки називаються полігоном накопиченої частоти або полігоном накопиченої відносної частоти. У статистиці також їх називають огівою або кумулятивною кривою. Полігон накопиченої частоти зручно використовувати у цілому ряді задач статистики.


