
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виписати формулу для обчислення імовірності хоча б однієї з декількох подій, незалежних у сукупності.Пояснити зміст позначень. Навести приклади.Содержание книги
Поиск на нашем сайте
Події називаються незалежними якщо імовірність появи однієї не залежить від появи або не появи іншої. P=a/n-імовірність певної події,а-кількісь наслідків єксперименту, коли відбвається певна подія. N-загальна кількість наслідків експерименту.Тож імовірність появи хоча б одієї події буде Р=Р1+Р2...+Рn,де Р1,Р2, Рn імовірності появи незалежних подій. Приклад:кидання двох монет, поява орла чи решки внаслідок киданя однієї монети не залежить від результату кидання другої монети. Потрібно додати що якщо події незалежні то умовна імовірність події дорівнює її безумовнії імовірності. 1.16. Вивести формули: а) повної імовірності; б) Байеса. Пояснити зміст позначень. Навести приклади застосування цих формул. Імовірність події А, яка може настати лише при умові появи однієї з несумісних подій В1,В2,В3..Вn, які утворюють повну групу, дорівнює сумі добутків імовірностей кожної з цих подій на відповідну умовну імовірність події А. P(A)=P(B1)*PB1(A)+P(B2)*PB2(A)+...P(Bn)PBn(A). Це формула повної імовірності. P(A)-імовірність події А, P(B1)-імовірність події В1, PB1(A)-умовна імовірність події А при виконанні події В1. Приклад: В першій коробці 20 радіоламп, з них 18 стандартних, в другій – 10 ламп, з них 9 стандартних. З другої коробки навмання взята лампа і перекладена в першу. Формула Байєса:
PA(B1)=(P(Bi)*PBi(A))/(P(B1)*PB1(A)+P(B2)*PB2(A)+…+P(Bn)*PBn(A)).Пояснення букв як і для повної імовірності. Формули Байєса дозволяють переоцінити імовірність гіпотез, після того, як стає відомим результат випробовування, в результаті якого з’явилася подія А. Приклад: Деталі потрапляють на перевірку до одного з двох контролерів. Імовірність, що попаде до першого-0,6, що до другого-0,4. Імовірність того що деталь буде признана стандартною першим контролером-0,95. Другим-0,93. Деталь була признана стандартною. Яка імовірність того, що деталь перевірив перший контролер? Описати схему випробувань Бернулі. Записати формулу Бернулі.Навести приклади її застосування. Незалежні випробування. Нехай проводяться n випробувань, у кожному з яких подія А може відбутись або не відбутись. Якщо ця ймовірність у кожному випробуванні не залежить від того, відбулась вона в інших випробуваннях чи ні, то такі випробування називаються незалежними щодо події А. Згідно з означенням випробування також незалежні, якщо в кожному з них імовірність настання події А однакова. Імовірність того, що подія А відбудеться в кожному з незалежних випробувань, позначають
Формула застосовується, якщо n<=10. Приклад Монета кидається 3 рази, Р того, що «герб» випаде один раз n=3 А-«випадання герба» Р(А)=р= Р( K=1 А Р
1.18. С формулювати граничні теореми у схемі випробувань Бернулі. а)Пуассона. б) Локальну та інтегральну Лапласа. Теорема Пуасона Нехай проводиться n випробувань, кожному з яких ймовірність настання події А є сталою величиною. Якщо кількість випробувань прямує до нескінченності, а ймовірність настання події А Зауваження Якщо кількість випробувань n є дуже велике число n>1000, а р є дуже мале p<0,01, то Р Задача Перевозиться 1000 пляшок від А до В. Імовірність того, що будь-яка пляшка розібьється =0,001. Знайти Р того, що під час перевезення розіб’ється тільки одна пляшка. Р
Локальна теорема Лапласа(Муавра-Лапласса) Якщо виконуються умови схеми випробувань Бернуллі: -проводиться n випробувань,кожному з яких є стала і=р. -при достатньо великих n ймовірність того,що n випробувань подія А з`явиться рівно к-раз. Р а Рівність є тим точнішою,чим більше випробувань n проведено. Ф-я 1.Якщо х=0,то 2.Якщо х 3.Ф-я Ф-я Приклад. У пологовому будинку нараховано 100 дітей,яка ймовірність того,що серед цих 100 дітей 60 хлопців. Якщо Р(А)=0,55 n=100.k=60.А= «народження хлопчика».Р=0,55.q=0,45 Р Х= Зауваження: Таке правило локальна теорема Лаппаса використовується якщо кількість випробувань n>50, а ймовірність р
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.233.69 (0.009 с.) |


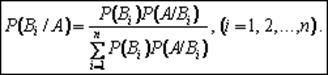
 а ймовірність настання протилежної події
а ймовірність настання протилежної події 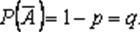 Для розв’язування задач на повторні незалежні випробування застосовують такі формули і теореми.Формула Бернуллі. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:
Для розв’язування задач на повторні незалежні випробування застосовують такі формули і теореми.Формула Бернуллі. Імовірність того, що в n незалежних випробуваннях, у кожному з яких імовірність Р(А) = р, подія А відбудеться m раз, подається так:
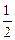
 )=
)=  =
= 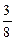
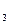 (1)= C
(1)= C  *(0,5)
*(0,5) 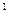 *(0,5)
*(0,5)  , то ймовірність того, що Р
, то ймовірність того, що Р  (k)
(k)  ,де
,де 

 (1)
(1) 

 (k)
(k) 
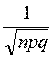 *
*  (х), де х=
(х), де х= 
 ,
,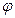 (х)=
(х)=  *е
*е  -називається локальною функцією Лапласса.(
-називається локальною функцією Лапласса.( ,то ф-я
,то ф-я  (60)
(60) 
 =
= 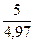 =1
=1 
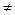 0, р
0, р 


