
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Cформулювати предмет теорії імовірностей?Содержание книги
Поиск на нашем сайте
Cформулювати предмет теорії імовірностей? Предметом теорії імовірності є вивчення імовірних закономірностей масових однорідних випадкових подій. Подія – явище, що здійснюється або не здійснюється за час проведення експерименту. Експериментом або випробуванням наз. реалізація певної сукупності умов, в результаті якої настає або відбувається певний наслідок або подія. Подія називається вірогідною, якщо ця подія під час проведення випробування обов’язково відбудеться. Приклад: Наприклад, якщо в урні є лише білі кулі, то добування білої кулі з урн є достовірна подія. Подія називається випадковою, якщо у разі проведення випробування ця подія може відбуватись або не відбуватись. Подія називається неможливою, якщо під час проведення випробування вона не може відбутися. Приклад: кидання монети: випаде герб – випадкова, ребро – неможлива; кидання гральної кістки: кістка впаде на грань – вірогідна.
Дати означення підмножини, скінченної, нескінченної, зліченої, незліченої, упорядкованої та неупорядкованої множин. Навести приклад. Підмножина – частина множини. Множина називається скінченна (нескінченна) якщо вона містить скінченне (нескінченне) число елементів. Нескінченна множина називається зліченою (незліченою) якщо її елементи можна (не можна) пронумерувати. Приклад: А={1,2,3,5,8}- скінченна B={2,9,6,8,....}-нескінченна Множина називається упорядкованою (неупорядкованою) якщо її елементи повинні (неповинні) бути розташовані у певному порядку. Упорядковані множини відрізняються одна від одної набором елементів з яких вони скл. або розташуванням цих елементів. Неупорядковані відр. тільки набором елементів незалежно від порядку розташування. Наприклад.: 1,2,3- упорядкована; 3,6,1- неупорядкована. Дати означення об’єднання(або суми), перетину(або добутку) та різниці множин. Навести основні властивості цих операцій та відповідні приклади. Сумою (об’єднанням, А ﮞ В= А+В) 2-х множин А і В наз. така множина С, елементи якої є всі елементи множини А і В. Різницею А і В наз. С, яка складається з тих елементів множини А, які не входять в множину В. Добутком (перетин А∩В=А*В) 2-х множин А і В наз. така множина С, елементи якої є елементами множини А і В.
Пр. А={1,2,4,8}, B={1,2,6,8,9,10} А ﮞ В={1,2,8}, А∩В={1,2,4,6,8,9,10}, A-B={4} Дати означення розміщення, переставлення та сполучення. Записати формули для обчислення числа цих сполук.Пояснити зміст позначень та навести приклади. Перестановками (Pn) наз. будь-яка впорядкована множина, яка скл. з N елементів. Pn=n! де n!=1,2,3…n. Приклад: Скільки тризначних чисел можна скласти з цифр 1,2,3, якщо кожна цифра входить до зображення числа тільки один раз? P3=3!=3*2*1=6. Розміщення (Аnk)- будь-яка впорядкована півмножина з n елементів даної множини, яка містить k елементів, k ≤n. Розміщення відрізняється або складом елементів або їх порядком.
Приклад: в 11 – му класі 35 учнів вони обмінялися один з одним фотокартками скільки всього фотокарток було роздано?
Сполучення (Сnk)- будь-яка півмножина з n елементів даної множини, яка містить k елементів. Одне сполучення відрізняється одне від одного лише складом елементів
Приклад: Скількома різними способами можна вибрати з 15 чоловік делегацію в складі 3 осіб.
Записати формулу, що пов’язує число переставлень, сполучень та розміщень. Сформулювати правила суми та добутку. Навести приклади. Числа перестановок, сполучень та розміщень пов’язані нерівністю: Аnk= Pk Сnk Нехай множина А містить ел. Аі, де і змінюється від 1 до n; множина В, вj (j=1до k) Правило сум: якщо множини А і В не перетинаються, тобто А∩В=0, то множина, яка є об’єднанням цих множин АﮞВ містить n+k елементів. Правило добутку: множина С усіх можливих пар (аі, вj) містить n*k елементів.
Дати означення випадкового експерименту,його елементарного наслідку, проостору елементарних наслідків. Навести приклади випадкових експерементів ізскінченним, зліченим та незліченим просторами елементарних наслідків. Експериментом або випробуванням наз. реалізація певної сукупності умов в результаті якої настає або відбувається певний наслідок або подія. Експеримент наз. детермінованим, якщо в результаті його проведення завжди настає або не настає певна подія, яка також наз. детермінованою. При цьому якщо детермінована подія настає або не настає вона наз. достовірною і позначається літерою U або неможливою (V). Події наз. рівно можливими якщо немає підстав вважати, що поява однієї з них є більш можливим за появу другої (напр. поява того чи іншого числа очків на гральних костях – рівно можливі події). Експеримент наз. випадковим, якщо в результаті його проведення деяка подія може настати, а може і не настати. При цьому допускається, що цей експеримент може (не може) бути повторений скільки завгодно раз. Подія, що настає в результаті невизначеного (випадкового) експерименту наз. випадковою.
Елементарним наслідком випадкового експерименту називається така подія, яка не може бути сумою інших наслідків цього ж експерименту. Елементарні наслідки (всі) утворюють повну групу подій і називаються простором елементарних наслідків. Приклад: скінчений простір елементарних наслідків – постріли по мішені, до першого влучення. Незлічений простір елементарних наслідків – час роботи прилада, тому що залежить від умов його виробництва.
Сформулювати класичне визначення імовірності випадкової події, записати відповідну формулу і пояснити зміст позначень. Навести приклади.Назвати основні фактори, що обмежують застосування класичного визначення імовірності. Імовірність появи події А називають співвідношення числа сприятливих наслідків (m) до числа всіх можливих наслідків (n). Р(А)=m/n. Подія наз. випадковою, якщо в результаті випробування вона може відбутися або не відбутися. Імовірність події є численна міра степеня об’єктивної можливості цієї події. (Класичне) Імовірність події А дорівнює відношенню числа елементарних наслідків, які сприяють появі події А, до загального числа усіх єдиноможливих та рівноможливих елементарних наслідків.
Теорема Пуасона Нехай проводиться n випробувань, кожному з яких ймовірність настання події А є сталою величиною. Якщо кількість випробувань прямує до нескінченності, а ймовірність настання події А Зауваження Якщо кількість випробувань n є дуже велике число n>1000, а р є дуже мале p<0,01, то Р Задача Перевозиться 1000 пляшок від А до В. Імовірність того, що будь-яка пляшка розібьється =0,001. Знайти Р того, що під час перевезення розіб’ється тільки одна пляшка. Р
Локальна теорема Лапласа(Муавра-Лапласса) Якщо виконуються умови схеми випробувань Бернуллі: -проводиться n випробувань,кожному з яких є стала і=р. -при достатньо великих n ймовірність того,що n випробувань подія А з`явиться рівно к-раз. Р а Рівність є тим точнішою,чим більше випробувань n проведено. Ф-я 1.Якщо х=0,то 2.Якщо х 3.Ф-я Ф-я Приклад. У пологовому будинку нараховано 100 дітей,яка ймовірність того,що серед цих 100 дітей 60 хлопців. Якщо Р(А)=0,55 n=100.k=60.А= «народження хлопчика».Р=0,55.q=0,45 Р Х= Зауваження: Таке правило локальна теорема Лаппаса використовується якщо кількість випробувань n>50, а ймовірність р
Дати означення функції випадкової величи. Навести спосіб побудови закону розподілу функції д.в.в. Записати формулу для знаходження щільності розподілу імовірностей функції н.в.в.Навести приклади.пояснити зміст позначень. Н.В.В. Нехай х-дійсне число. Імовірність події, що Х прийме значення, менше х (Х <х), позначимо F(x)-функцією від х. Функцією розподілу називають функцію F(x), обозначаючу ймовірність того, що випадкова величина Х в результате випробування прийме значення, менше х, т.е. F(x)=P(X<x). Геометричний зміст: F(x)-ймовірність того, що, випадкова величинна прийме значення, котре зображається на числовій прямій точкою, розташованій лівіше точки х. Законом розподілу дискретної випадкової величини є відношення між можливими значеннями і їх імовірностями. Задаєтся таблично, аналітично, графічно. Приклад: В лотереї 100 білетів. Розігрують один виграш в 50 грн. і 10 виграшів по 1 грн.Найти закон розподілу випадкової величини Х-вартість виграшуу для власника одного білета. Розв’язок: X: x Закон розподілу Х(50,10,0), р(0,01;0,1;0,89). Щільніссть розподілу імовірностей н.в.в. Х називають функцію f(x)-першу похідну від функції розподілу F(x): f(x)= F’(x) функція розподілу. Для опису рлзподілу д.в.в. неприймається. Приклад: Дано: F(x)= 0, x<0 x2/81 0<x<=9 1 x>9 f(x)=F’(x) f(x)= 2x/81 x e (0;9] 0 x не належить (0;9] Сформулювати і обгрунтувати взаємозалежність між точністю інтервальної оцінки, її надійностю та обсягом вибірки. Вивести формули для обчислення кінців надійного інтервалу для оцінки середнього квадратичного відхилення нормального розподілу. Пояснити зміст позначень. Інтервальною оцінкою середнього квадратичного відхилення σ нормально розподіленого кількісної ознаки Х по “виправленому” вибірковому середньому квадратичному відхиленню s є довірчий інтервал s(1 – q)< σ<s (1+q) при q<1 0< σ < s (1+q) при q>1, де q знаходять по табл. за заданими n і Cформулювати предмет теорії імовірностей? Предметом теорії імовірності є вивчення імовірних закономірностей масових однорідних випадкових подій. Подія – явище, що здійснюється або не здійснюється за час проведення експерименту. Експериментом або випробуванням наз. реалізація певної сукупності умов, в результаті якої настає або відбувається певний наслідок або подія.
Подія називається вірогідною, якщо ця подія під час проведення випробування обов’язково відбудеться. Приклад: Наприклад, якщо в урні є лише білі кулі, то добування білої кулі з урн є достовірна подія. Подія називається випадковою, якщо у разі проведення випробування ця подія може відбуватись або не відбуватись. Подія називається неможливою, якщо під час проведення випробування вона не може відбутися. Приклад: кидання монети: випаде герб – випадкова, ребро – неможлива; кидання гральної кістки: кістка впаде на грань – вірогідна.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.23.103 (0.008 с.) |





 де m- число елементарних наслідків, що сприяють події А, n- число усіх єдиноможливих та рівноможливих наслідків. Зауваження: 1.класичне означення імовірності має місце лише тоді, коли m та n скінчені, усі елементарні наслідки рівноможливі. Якщо множина елементарних наслідків нескінчена, то цією формулою користуватися не можна.2. Вимога рівноможливості всіх елементарних наслідків експерименту.
де m- число елементарних наслідків, що сприяють події А, n- число усіх єдиноможливих та рівноможливих наслідків. Зауваження: 1.класичне означення імовірності має місце лише тоді, коли m та n скінчені, усі елементарні наслідки рівноможливі. Якщо множина елементарних наслідків нескінчена, то цією формулою користуватися не можна.2. Вимога рівноможливості всіх елементарних наслідків експерименту. , то ймовірність того, що Р
, то ймовірність того, що Р  (k)
(k)  ,де
,де 

 (1)
(1) 

 (k)
(k) 
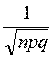 *
*  (х), де х=
(х), де х= 
 ,
,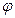 (х)=
(х)=  *е
*е  -називається локальною функцією Лапласса.(
-називається локальною функцією Лапласса.( ,то ф-я
,то ф-я  (60)
(60) 
 =
= 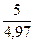 =1
=1 
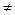 0, р
0, р  =50, x
=50, x  =1, x
=1, x  =0. p
=0. p  =0,01
=0,01  =0,01
=0,01  =1(
=1( =0,89.
=0,89. ; n – об’єм вибірки,
; n – об’єм вибірки,  )=
)=  або P(s -
або P(s - 


