
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дати означення корельованості (некорельованості) двох в.в. Пояснити різнцю і зв’язок між корельованістю (некорельованістю) і залежністю двох в.в.Содержание книги
Поиск на нашем сайте Важливу роль у дослідженнях систем відіграє мішаний центральний момент другого порядку Легко вивести робочу формулу для обчислення кореляційного моменту
де
і Зв’язок між корел-тю(некорел-тю) та залежністю: якщо Х, Y некорельовані μ xy=0, то залежність невідома. якщо Х, Y корельовані, то вони залежні якщо X, Y незалежні, то вони некорельовані X, Y =0 якщо X, Y залежні, то вони можуть бути як корельованими так і некорельованими μ xy – індикатор залежності і незалежності X, Y Різниця: із незалежності 2 величин слідує їх некорельованість, але із некорельваності неможна зробити висновок о незалежності цих величин
Вивести рівняння лінійної середньоквадратичної регресії Y на Х(Х на Y). Пояснити зміст позначень.Дати означення коефіцієнту регресії, залишкової дисперсії та пояснити, що вони характеризують. Лінійна середньоквадратична регресія Y на Х має вигляд g(X)=my+ Виведення: Введем у розгляд функцію двох незалежних аргументів F( Враховуючи, що М(Х – mx)=M(Y – my)=0, M[(X - mx)*(Y - my)]= μxy=r σxσy та виконав викладки, отримаємо F( Дослідим функцію F(
Звідси Легко впевнитися, що при цих значеннях g (X)= Коефіцієнт Підставимо знайдені значення Аналогічно можно отримати пряму середньоквадратичної регресії Х на Y X - mx=r Сформулювати теорему про корельованість складових нормально розподіленої двовимірної в.в. а) Мат. сподівання двохвимірної випадкової величини (X, Y) характеризує координати центру розподілу випадкової величини. Ці координати знаходять за формулами: Дисперсії DX та DY характеризують розсіювання випадкової точки (X, Y) вздовж координатних осей Ox та Oy, відповідно. Їх знаходять за формулами:
б) Условным мат. ожиданием ДСВ Y при X=x (x – определенное возможное значение X) называют произведение возможных значений Y на их условные вероятности: M(Y|X=x)= в) Для опису двохвимірної випадкової величини використовують також кореляційний момент (або коваріація): KXY=M((X-mX)(Y-mY))= г) коефіцієнт кореляції Коэффициенттом корреляции rxy случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин. Дати означення функції випадкової величи. Навести спосіб побудови закону розподілу функції д.в.в. Записати формулу для знаходження щільності розподілу імовірностей функції н.в.в.Навести приклади.пояснити зміст позначень. Н.В.В. Нехай х-дійсне число. Імовірність події, що Х прийме значення, менше х (Х <х), позначимо F(x)-функцією від х. Функцією розподілу називають функцію F(x), обозначаючу ймовірність того, що випадкова величина Х в результате випробування прийме значення, менше х, т.е. F(x)=P(X<x). Геометричний зміст: F(x)-ймовірність того, що, випадкова величинна прийме значення, котре зображається на числовій прямій точкою, розташованій лівіше точки х. Законом розподілу дискретної випадкової величини є відношення між можливими значеннями і їх імовірностями. Задаєтся таблично, аналітично, графічно. Приклад: В лотереї 100 білетів. Розігрують один виграш в 50 грн. і 10 виграшів по 1 грн.Найти закон розподілу випадкової величини Х-вартість виграшуу для власника одного білета. Розв’язок: X: x Закон розподілу Х(50,10,0), р(0,01;0,1;0,89). Щільніссть розподілу імовірностей н.в.в. Х називають функцію f(x)-першу похідну від функції розподілу F(x): f(x)= F’(x) функція розподілу. Для опису рлзподілу д.в.в. неприймається. Приклад: Дано: F(x)= 0, x<0 x2/81 0<x<=9 1 x>9 f(x)=F’(x) f(x)= 2x/81 x e (0;9] 0 x не належить (0;9]
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , який називається моментом зв’язку або кореляційним моментом (або коваріацією). Позначимо його
, який називається моментом зв’язку або кореляційним моментом (або коваріацією). Позначимо його  =
=  .
.
 обчислюється за формулами
обчислюється за формулами
 для дискретних випадкових величин
для дискретних випадкових величин для неперервних випадкових величин. Зауважимо, що
для неперервних випадкових величин. Зауважимо, що  (X – mx), де mx=М(Х), my=М(Y), σx=
(X – mx), де mx=М(Х), my=М(Y), σx=  , σy=
, σy=  , r=μxy/(σxσy) – коефіцієнт кореляції величин Х та Y.
, r=μxy/(σxσy) – коефіцієнт кореляції величин Х та Y. та
та 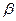 :
: +
+  - 2r σxσy
- 2r σxσy  ,
,  σxσy=0
σxσy=0 ,
, 
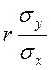 mx
mx X=
X=  -
-  mx+
mx+  X, або g(X)=my+
X, або g(X)=my+  наз. коефіцієнтом регресії Y на X
наз. коефіцієнтом регресії Y на X (1 – r2). Величину
(1 – r2). Величину  (1 – r2) наз. залишковою дисперсією в.в. Y відносно в.в. Х..Вона характеризує величину похибки, яку допускають при заміні Y лінійної функції g(X)=
(1 – r2) наз. залишковою дисперсією в.в. Y відносно в.в. Х..Вона характеризує величину похибки, яку допускають при заміні Y лінійної функції g(X)= 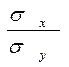 (Y- my), де r
(Y- my), де r  - коефіцієнт регресії Х на Y.Залишкова дисперсія
- коефіцієнт регресії Х на Y.Залишкова дисперсія 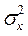 (1-r2) величини Х відносно Y.
(1-r2) величини Х відносно Y.


 Для непрерывных величин
Для непрерывных величин  , где
, где 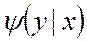 - условная плотность случайной величины Y при X=x.
- условная плотность случайной величины Y при X=x. . Корреляционным моментом μxy случайных величин X та Y называют мат. ожидание произведения отклонений этих величин. Для ДСВ:
. Корреляционным моментом μxy случайных величин X та Y называют мат. ожидание произведения отклонений этих величин. Для ДСВ:  Корреляционный момент служит для характеристики связи между величинами X и Y.
Корреляционный момент служит для характеристики связи между величинами X и Y.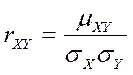 є кількісна характеристика залежності випадкових величин X та Y і часто використовуються в статистиці.
є кількісна характеристика залежності випадкових величин X та Y і часто використовуються в статистиці. =50, x
=50, x  =1, x
=1, x  =0. p
=0. p  =0,01
=0,01  =0,01
=0,01  =1(
=1( =0,89.
=0,89.


