Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття та основні властивості ймовірностіСодержание книги
Поиск на нашем сайте
Ймовірність події А – це число Р(А), яке характеризує шанси події відбутись чи не відбутись в даному випадковому експерименті. 1) 2) 3)
Класичне означення ймовірності Кажуть, що дана елементарна подія сприяє події А, якщо подія А відбувається кожний раз, коли ця елементарна подія є результатом випадкового експерименту. Припустимо, що множина елементарних подій скінченна і всі елементарні події рівноможливі (мають однакові ймовірності). Ймовірністю події А називається відношення числа елементарних подій, що сприяють події А, до числа всіх елементарних подій експерименту.
Відносна частота події Нехай випадковий експеримент повторювали n разів і при цьому у k іспитах відбулась подія А. Відношення Геометричні ймовірності Нехай в геометричну область G скінченної міри навмання кинута точка. Ймовірність попадання цієї точки в деяку область
Опитування з теорії
1.Що таке випадковий експеримент, випадкові події, елементарні події? 2.Як утворюється простір елементарних подій, як він позначається? 3.Як можна розглядати випадкові події по відношенню до простору елементарних подій? Що означає, що відбулась випадкова подія? 4.Які операції з подіями можна виконувати? Дати означення цих операцій. 5.Що таке ймовірність, які її основні властивості? 6.Дати класичне означення ймовірності. 7.Що називається відносною частотою події? 8.Що таке геометрична ймовірність?
Задача 1. Випробування полягає в однократному підкиданні симетричного грального кубика і спостереженні числа очок, що випали на верхній грані. Побудувати простір елементарних подій 1) подія А – випало парне число очок; 2) подія В – випало число очок, що ділиться на 3; 3) подія С – число очок, що випали, більше 3. В чому полягають події Розв’язання. Для симетричного грального кубика рівноможливим є випадання на верхній грані чисел 1, 2, …, 6. Позначимо через 1)Розглянемо подію А. Вона відбувається, якщо на верхній грані випадуть числа 2, 4, 6. Виберемо з множини 2) Подія В відбувається, якщо випадають числа 3 і 6. Виберемо з множини 3) Подія С відбувається, якщо випадають числа 4, 5, 6. Виберемо з множини Подія Зауваження. Суму чи добуток подій можна знаходити, використовуючи операції об’єднання чи перерізу відповідних множин: Задача 2. Нехай А, В, С – випадкові події, що можуть відбутися в одному експерименті. Описати такі події: 1) з подій А, В, С відбулась тільки В (подія D); 2) відбулась хоч одна подія з подій А, В, С (подія Е). Розв’язання. 1) Подія D полягає в тому, що з трьох подій А, В, С відбулась тільки подія В, це означає, що події А і С не відбулись, тобто одночасно з В відбулись протилежні події до подій А і С. Тому подію D можна представити так: 2) Подію Е легко представити, використовуючи операцію додавання подій: Задача 3. Робітник виготовив три деталі. Нехай подія 2) хоча б одна з деталей має дефект (подія В); 4) точно дві деталі дефектні (подія D); 6) не більше двох деталей дефектні (подія F). Розв’язання. 1) Подія А полягає в тому, що перша деталь не дефектна, одночасно друга деталь не дефектна і третя деталь не дефектна, тобто 2) Подія В полягає в тому, що або перша деталь дефектна, або друга деталь дефектна, або третя деталь дефектна, тобто 3) Подія С полягає в тому, що або перша деталь дефектна, а друга і третя деталі не дефектні, або друга деталь дефектна, а перша і третя не дефектні, або третя деталь дефектна, а перша і друга не дефектні, тому 4) Подія D полягає в тому, що одна з деталей не дефектна, в той час, як дві інші – дефектні. Не дефектною може бути або перша деталь (дві інші – дефектні), або друга (дві інші – дефектні), або третя (дві інші – дефектні), тому 5) Подію Е можна отримати так само, як і подію D, якщо видалити риски над тими подіями, де вони є, і поставити риски там, де їх нема: 6) Подія F полягає в тому, що або зовсім нема дефектних деталей (подія А), або тільки одна деталь дефектна (подія С), або точно дві деталі дефектні (подія D), тому Задача 4. Монету підкидають двічі. Описати простір елементарних подій. Описати події: А – принаймні один раз з’явиться герб, В – при другому підкиданні з’явиться герб. Знайти ймовірності подій А та В, вважаючи, що всі елементарні події рівноможливі. Розв’язання. Будемо випадання герба позначати символом Г, випадання цифри позначати символом Ц, послідовне випадання герба і цифри у вказаному порядку позначати символом ГЦ і т.д. Використовуючи ці позначення, опишемо простір елементарних подій: Проаналізуємо, які елементарні події сприяють події В. Це такі елементарні події, в символічному двобуквеному записі яких буква Г зустрічається на другому місці, тому Задача 5. Монету підкидають доти, поки вона не випаде підряд двічі однією і тією ж самою стороною. Описати простір елементарних подій. Описати події: А – експеримент потребує чотири підкидання; В – експеримент закінчиться до четвертого підкидання. Розв’язання. Випадання герба позначимо символом Г, випадання цифри –символом Ц, послідовне випадання герба і цифри у вказаному порядку позначимо символом ГЦ і т.д. Використовуючи ці позначення, опишемо простір елементарних подій
Задача 6. З цифр 1,2,3,4 спочатку вибирають одну; потім з трьох цифр, що залишились, вибирають другу. Описати простір елементарних подій. Вважаючи, що всі елементарні події рівноможливі, знайти ймовірність події Розв’язання. Простір елементарних подій складається з пар чисел
Задача 7. Показати, що Розв’язання. Подія, яку описує ліва частина рівняння – «не відбулась подія А + В», тобто не відбулись ні А, ні В. Це означає, що відбулись одночасно протилежні події –
Розв’язання. Елементарною подією в даному експерименті є будь-яка пара значень Задача 9. В одиничний квадрат навмання кинуто точку. Яка ймовірність, що точка буде віддалена від центра квадрата на відстань менше ніж 1/3, якщо відомо, що від кожної із сторін квадрата вона віддалена більше ніж на 1/6?
Задача 11. Експеримент полягає в однократному підкиданні грального кубика. Представити простір елементарних подій Розв’язання. Таке представлення можна зробити декількома способами. Для Для Для Задача 12. Для спортсмена відносна частота влучення в ціль 0,9. Скільки було зроблено пострілів, якщо одержано 7 промахів? Розв’язання. Відносна частота влучень 0,9 означає, що з 10 пострілів буде 9 влучень і 1 промах. Щоб отримати 7 промахів, потрібно зробити 70 пострілів.
Задачі для аудиторної та самостійної роботи
1. Підкидають монету, а після цього підкидають гральний кубик. Описати простір елементарних подій експерименту. Знайти ймовірності подій: А – випало парне число очок; В – випав герб; С – випали герб і парне число очок. Відповідь: 2. Гральний кубик підкидають двічі. Описати простір елементарних подій. Описати події: А – сума очок, які випали, дорівнює 6; В – принаймні один раз з’явиться 6. Відповідь: 3. Монету підкидають доти, поки не випаде герб. Описати простір елементарних подій. Відповідь: 4. З цифр 1, 2, 3, 4, 5 навмання вибирають одну цифру. Яка ймовірність, що вибрано парну цифру (подія А), просту цифру (подія В)? Відповідь: 5. 3 цифр 1, 2, 3, 4, 5 спочатку вибирають одну цифру; потім з чотирьох цифр, що залишились, вибирають ще одну. Описати простір елементарних подій. Вважаючи, що всі події рівноможливі, знайти ймовірності подій: А – перший раз вибрали парну цифру; В – другий раз вибрали парну цифру; С – обидва рази вибрали парні цифри. Відповідь: 6. Нехай А, В, С – випадкові події, що можуть відбутися в одному експерименті. Використовуючи операції над подіями, описати такі події: 1) настали всі три події; 2) настали тільки дві події; 3) настала тільки одна подія; 4) не настала жодна подія; 5) настало не більше двох подій; 6) настало не більше однієї події. 7. Прилад складається з трьох елементів, кожний з яких може працювати або відмовити. Описати простір елементарних подій. Нехай подія А – відмовив перший елемент; подія В – відмовили два елементи; подія С – працює не більше одного елемента. Описати події 8. У круг радіуса Відповідь: 9. В квадрат із стороною а вписано круг. Знайти ймовірність того, що точка, навмання кинута в квадрат, попаде в круг. Відповідь: 10. В круг радіуса а вписано квадрат, в цей квадрат вписано круг. Знайти ймовірність того, що точка, навмання кинута в більший круг, попаде в менший круг. Відповідь: 11. При тестуванні електроприладів відносна частота непридатних приладів виявилась рівною 0,03. Скільки було перевірено приладів, якщо виявлено 9 непридатних? Відповідь: 300. Практичне заняття 2
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 Ймовірність – це число, яке не може бути менше нуля і більше 1.
Ймовірність – це число, яке не може бути менше нуля і більше 1. Ймовірність неможливої події
Ймовірність неможливої події 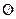 дорівнює нулю.
дорівнює нулю. Ймовірність достовірної події
Ймовірність достовірної події  дорівнює 1.
дорівнює 1. називається відносноючастотою події А і позначається
називається відносноючастотою події А і позначається  Якщо при великих значеннях n відносна частота мало відрізняється від деякого числа Р, то кажуть що подія А є статистично стійкою і число Р – її ймовірність.
Якщо при великих значеннях n відносна частота мало відрізняється від деякого числа Р, то кажуть що подія А є статистично стійкою і число Р – її ймовірність. називається геометричною ймовірністю і шукається за формулою
називається геометричною ймовірністю і шукається за формулою  де
де  – міра відповідної геометричної області.
– міра відповідної геометричної області.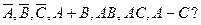
 елементарну подію, що на верхній грані кубика випало
елементарну подію, що на верхній грані кубика випало  очок. Тоді простір елементарних подій
очок. Тоді простір елементарних подій 
 .
. .
. .
. відбувається, коли випадає непарне число очок, а саме: 1, 3, 5, тому
відбувається, коли випадає непарне число очок, а саме: 1, 3, 5, тому  Подія
Подія  відбувається, коли випаде число, що не ділиться на 3, це: 1, 2, 4, 5, тому
відбувається, коли випаде число, що не ділиться на 3, це: 1, 2, 4, 5, тому  Подія
Подія  відбувається, коли випадають числа, не більші за 3,тобто: 1, 2, 3, тому
відбувається, коли випадають числа, не більші за 3,тобто: 1, 2, 3, тому  . Подія
. Подія  відбувається, коли випаде число, що ділиться або на 2, або на 3, або і на 2 і на 3 одночасно, тобто випадуть числа 2, 3, 4, 6, тому
відбувається, коли випаде число, що ділиться або на 2, або на 3, або і на 2 і на 3 одночасно, тобто випадуть числа 2, 3, 4, 6, тому 
 Подія АВ відбувається, якщо випаде число очок, що ділиться на 2 і на 3 одночасно, це 6, тому
Подія АВ відбувається, якщо випаде число очок, що ділиться на 2 і на 3 одночасно, це 6, тому 
 Подія
Подія  відбувається, коли випаде парне число очок, яке більше 3, це 4 і 6, тому
відбувається, коли випаде парне число очок, яке більше 3, це 4 і 6, тому  Подія
Подія  відбувається, коли випаде парне число очок, яке не більше 3, тобто число 2, тому подія
відбувається, коли випаде парне число очок, яке не більше 3, тобто число 2, тому подія  .
.
 ;
; 

 .
. .
.

 полягає в тому, що i -та деталь має дефект. Використовуючи операції над подіями, записати такі події:
полягає в тому, що i -та деталь має дефект. Використовуючи операції над подіями, записати такі події: .
. .
. .
. .
. .
.


 .
. , маємо 4 елементарні події як можливі наслідки випробування. Опишемо подію А. Подивимось, які елементарні події сприяють події А. Це такі елементарні події, в символічному двохлітерному записі яких літера Г зустрічається або один, або два рази, тому
, маємо 4 елементарні події як можливі наслідки випробування. Опишемо подію А. Подивимось, які елементарні події сприяють події А. Це такі елементарні події, в символічному двохлітерному записі яких літера Г зустрічається або один, або два рази, тому  .
. . Знайдемо ймовірності подій А і В, використовуючи класичне означення ймовірності. Оскільки є всього 4 рівноможливі елементарні події і події А сприяють три з них, то
. Знайдемо ймовірності подій А і В, використовуючи класичне означення ймовірності. Оскільки є всього 4 рівноможливі елементарні події і події А сприяють три з них, то  . Аналогічно, події В сприяють дві елементарні події, тому
. Аналогічно, події В сприяють дві елементарні події, тому 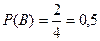 .
. Подія
Подія  має вигляд
має вигляд 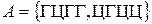 ; подія В описується так
; подія В описується так  .
. , тобто
, тобто , всього 12 елементарних подій. Подія
, всього 12 елементарних подій. Подія 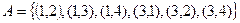 , всього 6 елементарних подій. Шукана ймовірність
, всього 6 елементарних подій. Шукана ймовірність  .
. , де А і В – події, що відбуваються в одному експерименті.
, де А і В – події, що відбуваються в одному експерименті. .
. Задача 8. Експеримент полягає у вимірюванні двох величин, які набувають значень з відрізка
Задача 8. Експеримент полягає у вимірюванні двох величин, які набувають значень з відрізка  . Описати простір елементарних подій.
. Описати простір елементарних подій. , де
, де 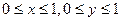 , тобто довільна точка на площині хОу, яка попадає в квадрат
, тобто довільна точка на площині хОу, яка попадає в квадрат  . Таким чином, простір елементарних подій – це квадрат
. Таким чином, простір елементарних подій – це квадрат  Розв’язання. З умови задачі випливає, що точка, кинута навмання в одиничний квадрат, попала в квадрат (див. рис. 2) із стороною
Розв’язання. З умови задачі випливає, що точка, кинута навмання в одиничний квадрат, попала в квадрат (див. рис. 2) із стороною  Міра цієї області (квадрата) – це його площа
Міра цієї області (квадрата) – це його площа  . Щоб визначити ймовірність того, що точка буде віддалена від центра одиничного квадрата на відстань менше ніж 1/3, потрібно знайти міру (площу)
. Щоб визначити ймовірність того, що точка буде віддалена від центра одиничного квадрата на відстань менше ніж 1/3, потрібно знайти міру (площу)  цієї області (геометричного місця точок з такою властивістю), і далі, використовуючи поняття геометричної ймовірності, поділити її на величину
цієї області (геометричного місця точок з такою властивістю), і далі, використовуючи поняття геометричної ймовірності, поділити її на величину  . Знайдемо
. Знайдемо 
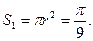 Тому шукана ймовірність
Тому шукана ймовірність 
 можна взяти таку повну групу подій:
можна взяти таку повну групу подій:  – випало непарне число очок;
– випало непарне число очок;  – випало парне число очок. Оскільки
– випало парне число очок. Оскільки  – це неможлива подія (число може бути або парним, або непарним, але не одночасно),
– це неможлива подія (число може бути або парним, або непарним, але не одночасно),  – достовірна подія (завжди випадає або парне, або непарне число), за означенням це повна група подій.
– достовірна подія (завжди випадає або парне, або непарне число), за означенням це повна група подій. можна взяти таку повну групу подій:
можна взяти таку повну групу подій:  –випало складене число очок. При цьому виконуються умови: 1)
–випало складене число очок. При цьому виконуються умови: 1)  виберемо за
виберемо за 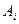 елементарну подію
елементарну подію  (див. задачу 1). При цьому елементарні події попарно несумісні (їх добуток неможлива подія) і їх сума дає достовірну подію (завжди відбувається одна з елементарних подій).
(див. задачу 1). При цьому елементарні події попарно несумісні (їх добуток неможлива подія) і їх сума дає достовірну подію (завжди відбувається одна з елементарних подій).

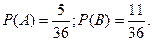
 .
.
 ;
; 
 . Відповідь:
. Відповідь:  ;
;
 ;
; 
 .
.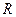 навмання кидають точку. Яка ймовірність, що відстань від цієї точки до центра круга не перевищує
навмання кидають точку. Яка ймовірність, що відстань від цієї точки до центра круга не перевищує  ?
?