
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула повної ймовірності. Формули Байєса. Розрахунок надійності простих технічних системСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Ймовірність події А, яка може відбутися при умові появи однієї з подій (гіпотез) H 1, H 2, …, Hn, що утворюють повну групу,обчислюється за формулою повної ймовірності
де Р (Hі) - ймовірність гіпотези Hі , Оскільки події H 1, H 2, …, Hn утворюють повну групу подій, то
(апостеріорна ймовірність) з урахуванням появи події А обчислюється за формулою Байєса
Нехай технічна система складається з двох елементів, які працюють і виходять з ладу незалежно один від одного. Введемо позначення для подій Аі = “безвідмовна робота протягом часу Т і -го елемента” (і = 1, 2), А = “безвідмовна робота протягом часу Т системи”. Ймовірність рі = Р (Аі) будемо називати надійністю і -го елемента 1) Очевидно, що в цьому випадку А = А 1 А 2 і надійність системи обчислюється за формулою р = Р (А) = Р (А 1 А 2) = Р (А 1) Р (А 2) = р 1 р 2, або р = р 1 р 2. Якщо відмова системи відбувається при одночасній відмові обох елементів, то це відповідає паралельному з’єднанню елементів (рис. 4). В цьому випадку А = А 1 + А 2 і надійність системи обчислюється за формулою
р = Р (А) = Р (А 1 + А 2) = Р (А 1) + Р (А 2) – Р (А 1 А 2) = = Р (А 1) + Р (А 2) – Р (А 1) Р (А 2) = р 1 + р 2 – р 1 р 2, або р = р 1+ р 2 - р 1 р 2.
Аналіз більш складних технічних систем та обчислення їх надійності проводять за допомогою теорем додавання і множення ймовірностей.
Опитування з теорії 1. Записати формулу повної ймовірності. 2. Які умови мають виконуватися для подій (гіпотез) H 1, H 2, …, Hn? 3. Записати формулу Байєса. 4. В чому полягає відмінність між апріорною та апостеріорною ймовірністю гіпотези? 5. Що називають надійністю деталі, ділянки електричного кола, елемента технічної системи і т.і.? 6. Як обчислюється надійність ділянки системи з послідовно з”єднаними та з паралельно з”єднаними елементами?
2) Задача 1. Прилад може належати до однієї з трьох партій з імовірностями р 1, р 2 і р 3, де р 1 = 0,2, р 2 = 0,5 і р 3 = 0,3. Ймовірність того, що прилад пропрацює без відмов заданий час для цих партій відповідно дорівнює 0,8; 0,6 і 0,5. Обчислити ймовірність того, що навмання взятий прилад пропрацює заданий час. Розв”язання. Введемо позначення подій А = “ прилад пропрацює заданий час “, Hі = “ прилад належить до і -ї партії” (і = 1, 2, 3). Події H 1, H 2, H 3 утворюють повну групу подій, тому можна застосувати формулу повної ймовірності Р (А) = Р (H 1) З умови задачі маємо
Отже, шукана ймовірність дорівнює Р (А) = 0,2·0,8 + 0,5·0,6 + 0,3·0,5 = 0,61.
Задача 2. На склад надходять однакові радіодеталі, виготовлені на двох дільницях цеху. Відомо, що з першої дільниці поступає 35 % деталей, з другої – 65 %.Ймовірність виготовлення деталі вищої якості на першій дільниці дорівнює 0,9, на другій – 0,8. Знайти ймовірність того, що дві навмання взяті радіодеталі будуть вищої якості. Розв”язання. Введемо позначення подій А = “ взяті зі складу дві радіодеталі вищої якості “, А 1 = “ взята навмання радіодеталь виготовлена на першій дільниці “, А 2 = “ взята навмання радіодеталь виготовлена на другій дільниці “. Подія А може відбутись при виконанні однієї з наступних гіпотез: H 1= “ обидві взяті деталі виготовлені на першій дільниці ”; H 2= “ обидві взяті деталі виготовлені на другій дільниці”; H 3= “одна взята радіодеталь виготовлена на першій дільниці, а друга на другій дільниці”. З умови задачі знаходимо ймовірності гіпотез і умовні ймовірності події А при даних гіпотезах: Р (H 1) = Р (А 1 А 1) = 0,35×0,35 = 0,1225; Р (H 2) = Р (А 2 А 2) = 0,65×0,65 = 0,4225; Р (H 3) = Р (А 1 А 2) + Р (А 2 А 1) = 2×0,35×0,65 = 0,455;
За формулою повної ймовірності знаходимо ймовірність події А Р (А) = Р (H 1) + 0,4225×0,64 + 0,455×0,72» 0,7. Задача 3. Запобіжник в електричному колі відмовляє при короткому замиканні в електронній лампі з імовірністю 0,4, при замиканні в обмотці трансформатора – з імовірність 0,6, при пробої конденсатора – з імовірністю 0,8, з інших причин – з імовірністю 0,3. Апріорні ймовірності цих подій дорівнюють відповідно 0,25; 0,15; 0,32; 0,28. Встановити найбільш імовірну причину відмови запобіжника після того, як така подія відбулася. Розв”язання. Нехай подія А полягає в тому, що запобіжник відмовив. Можна зробити чотири припущення (гіпотези) щодо причин відмови запобіжника: H 1= “ коротке замикання в електронній лампі ”; H 2= “ замикання в обмотці трансформатора ”; H 3= “ пробій конденсатора ”; H 4= “ інші причини ”. Події H 1, H 2, H 3, H 4 утворюють повну групу подій. За умовою задачі Р (H 1) = 0,25; Р (H 2) = 0,15; Р (H 3) = 0,32; Р (H 4) = 0,28;
Нам необхідно знайти і порівняти нові ймовірності гіпотез H 1, H 2, H 3, H 4 приумові, що подія А відбулась. За формулами Байєса маємо
3)
Порівнюючи знайдені ймовірності, бачимо, що найбільшою з них є ймовірність РА (H 3). Таким чином, найбільш імовірно, що запобіжник відмовив внаслідок пробою конденсатора. 4) Задача 4. Визначити надійність (ймовірність безвідмовної роботи протягом часу Т) ділянки технічної системи 5) якщо відомі ймовірності безвідмовної роботи протягом часу Т її елементів p 1 = 0,7; p 2 = 0,8; p 3 = 0,8; p 4 = 0,9. Розв’язання. Нехай Аі = “безвідмовна робота і -го елемента протягом часу Т ” р = Р (А) = Р [ А 1(А 2 + А 3 ) А 4] = Р (А 1) Р (А 2 + А 3 ) Р (А 4) = = Р (А 1) Р (А 4) [ Р (А 2) + Р (А 3 ) – Р (А 2 А 3)] = Р (А 1) Р (А 4) [ Р (А 2) + Р (А 3 ) – – Р (А 2 ) Р (А 3)] = 0,7×0,9(0,8 + 0,8 – 0,82) ≈ 0,6. Отже, шукана надійність ділянки системи р ≈ 0,6.
Задачі для аудиторної і самостійної роботи 1. В цеху працює 20 станків, серед яких 10 типу А, 6 типу В і 4 типу С. Ймовірність того, що якість деталі буде високою, для цих станків відповідно дорівнює 0,9; 0,8 і 0,7. Який відсоток високоякісних деталей випускає цех? Відповідь: 83%. 2. Прилад може працювати у двох режимах: нормальному і ненормальному. Нормальний режим спостерігається у 80% всіх випадків роботи приладу, ненормальний у 20%. Ймовірність виходу приладу з ладу за час Т в нормальному режимі дорівнює 0,1, в ненормальному – 0,7. Знайти ймовірність виходу приладу з ладу за час Т. Відповідь: 0,22. 3. В продаж надходять телевізори, виготовлені на трьох заводах. Продукція першого заводу містить 15% телевізорів з прихованим дефектом, другого – 8 % і третього - 5%. Обчислити ймовірність придбання справного телевізора, якщо в магазин надійшло 40% телевізорів з першого заводу, 25% з другого і 35% з третього. Відповідь: 0,9025. 4. В 15-ти екзаменаційних білетах міститься по два питання, які не повторюються. Студент знає 25 питань. Обчислити ймовірність того, що студент складе екзамен, якщо для цього достатньо відповісти на два питання з одного білета, або на одне питання з першого білета і на додаткове питання з другого білета. Відповідь: 190/203. 5. Два станки-автомати виготовляють однакові деталі, які поступають на один конвеєр. Продуктивність першого станка вдвічі більша за продуктивність другого. Перший станок виготовляє в середньому 60% деталей відмінної якості, другий-84%. Навмання взята з конвеєра деталь виявилась відмінної якості. Знайти ймовірність того, що ця деталь виготовлена першим станком. Відповідь: 10/17. 6. Число вантажних машин, що їдуть по шосе, на якому стоїть АЗС, відноситься до числа легкових авто, що їдуть по тому ж шосе, як 3:2. Ймовірність того, що буде заправлятись вантажна машина, дорівнює 0,1; для легкової машини ця ймовірність дорівнює 0,2. На заправку під’їхав автомобіль. Знайти ймовірність того, що це вантажна машина. Відповідь: 3/7. 7. Прилад складається з двох вузлів, робота кожного необхідна для роботи приладу в цілому. Ймовірність безвідмовної роботи за час Т для першого вузла дорівнює р 1, для другого – р 2. Прилад випробовувався протягом часу Т, в результаті чого виявлено, що він вийшов з ладу. Знайти ймовірність того, що відмовив тільки перший вузол, а другий працював без відмов. Відповідь: [(1 – p 1) p 2]/(1 – p 1 p 2). 8. В групі з 10 студентів, що прийшли на екзамен, 3 підготовлені відмінно, 4 – добре, 2 – задовільно, 1 – погано. В екзаменаційних білетах є 20 питань. Відмінно підготовлений студент може відповісти на всі 20 питань, добре підготовлений – на 16, задовільно – на 10, погано підготовлений – на 5. Викликаний навмання студент відповів на три випадково заданих питання. Знайти ймовірність того,що цей студент підготовлений: а) відмінно; б) погано. Відповідь: a) 0,58; б)0,002.
6) В задачах 9 – 11 визначити надійність (ймовірність безвідмовної роботи протягом часу Т) ділянки технічної системи, якщо відомі ймовірності р 1, р 2, … безвідмовної роботи протягом часу Т 1-го, 2-го, … її елементів. Вважається, що вихід з ладу протягом часу Т окремих елементів системи – незалежні події. Відмова ділянки послідовно з’єднаних елементів відбувається при відмові хоч одного з них. Ділянка паралельно з’єднаних елементів виходить з ладу, якщо відмовляють всі її елементи. 7) 9. p 1 = 0,8; p 2 = 0,9; p 3 = 0,8; p 4 = 0,9; p 5=0,7. Відповідь: 0,976. 10. p 1 = 0,7; p 2 = 0,7; p 3 = 0,7; p 4 = 0,8; p 5 = 0,8. Відповідь: 0,934. 11. p 1 = 0,9; p 2 = 0,8; p 3 = 0,8; p 4 = 0,7; p 5 = 0,9. Відповідь: 0,96. 12. Якою має бути надійність кожного з однакових вузлів, щоб надійність блоку з чотирьох послідовно з’єднаних вузлів була не меншою за 0,9? Відповідь: ³0,97. 13. Надійність приладу р = 0,5. Скільки резервних приладів слід підключити паралельно до кола, щоб надійність такої системи дорівнювала 0,9375? Відповідь: 4.
Практичне заняття 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.3 (0.007 с.) |

 ,
, (A) - умовна ймовірність події А при цій гіпотезі.
(A) - умовна ймовірність події А при цій гіпотезі. Якщо ймовірність події Hk
Якщо ймовірність події Hk  до проведення досліду (апріорна ймовірність) дорівнювала P (Hk), а в результаті досліду відбулась подія А, то умовна ймовірність гіпотези
до проведення досліду (апріорна ймовірність) дорівнювала P (Hk), а в результаті досліду відбулась подія А, то умовна ймовірність гіпотези 

 Якщо відмова системи відбувається при відмові хоч одного елемента, то це відповідає послідовному з’єднанню елементів (рис. 3).
Якщо відмова системи відбувається при відмові хоч одного елемента, то це відповідає послідовному з’єднанню елементів (рис. 3). + Р (H 2)
+ Р (H 2)  + Р (H 3)
+ Р (H 3)  .
.


 0,9×0,9 =0,81;
0,9×0,9 =0,81;  0,8×0,8 =0,64;
0,8×0,8 =0,64;  0,9×0,8 =0,72.
0,9×0,8 =0,72. 0,3.
0,3.
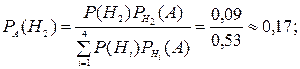


 , А = “безвідмовна робота ділянки системи протягом часу Т ”. Тоді Р (А 1) = р 1 = 0,7, Р (А 2) = Р (А 3) = 0,8; Р (А 4) = =0,9. Оскільки А = А 1(А 2+ А 3 ) А 4 і події А 1, А 2 + А 3 , А 4 – незалежні, то
, А = “безвідмовна робота ділянки системи протягом часу Т ”. Тоді Р (А 1) = р 1 = 0,7, Р (А 2) = Р (А 3) = 0,8; Р (А 4) = =0,9. Оскільки А = А 1(А 2+ А 3 ) А 4 і події А 1, А 2 + А 3 , А 4 – незалежні, то


