
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Випадкові потоки подій. Пуассонівський потікСодержание книги
Поиск на нашем сайте
Означення. Потоком подій називається послідовність подій, що відбуваються у випадкові моменти часу. Приклади потоків: замовлення, що надходять у довідкові бюро; виклики швидкої медичної допомоги; сигнали, що поступають на АТС; клієнти, що прибувають на підприємства побутового обслуговування; відмови елементів складної технічної системи тощо.
Будь-який потік можна розглядати як випадковий процес.
Важливими властивостями потоків подій є стаціонарність, відсутність наслідків та ординарність. Потік подій називається стаціонарним, якщо ймовірність появи k подій за проміжок часу тривалістю t залежить лише від k і t і не залежить від початку відліку.
Потік подій називається потоком без наслідків, якщо ймовірність появи k подій за будь-який проміжок часу не залежить від того, з’являлись чи не з’являлись події в моменти часу, що передують початку даного проміжку.
Потік подій називається ординарним, якщо ймовірність появи більш ніж однієї події за нескінченно малий проміжок часу є нескінченно малою величиною більш високого порядку, ніж імовірність появи тільки однієї події за той же малий проміжок часу.
Найпростішим (пуассонівским) називається потік подій, що має властивості стаціонарності, відсутності наслідків та ординарності. Нехай деяка подія А може наставати у випадкові моменти часу. Позначимо через X (t) число появ цієї події за проміжок часу від 0 до t. Випадковий потік (процес) X (t) буде пуассонівським, якщо виконують такі умови: 1) ймовірність k появ події А за час від T до T + t не залежить від T і не залежить від того, скільки разів наставала подія А до моменту T. Позначимо цю ймовірність через Pk (t). Отже,
Pk (t) = P (X (t) = k). (4.1)
2) якщо t ® 0, то P 1(t) = l t + o (t), Pk (t) = o (t) при k ³ 2, P 0(t) = 1 – l t + o (t), (4.2)
де l > 0 – деяка стала, а o (t) – нескінченно мала вищого порядку порівняно з t, тобто При виконанні умов 1, 2 ймовірність Pk (t) визначається формулою:
Кожний переріз пуассонівського процесу X (t) при заданому t є випадковою величиною, розподіленою за законом Пуассона з параметром l t. Стала l визначає середнє число появ події А за одиницю часу. Вона називається інтенсивністю потоку.
Розв’язування задач
Задача№1
Середнє число замовлень таксі (потік пуассонівський) протягом 1 хв дорівнює трьом. Знайти ймовірність того, що за 2 хв надійде п’ять замовлень.
Розв’язання За умовою l = 3, t = 2, k = 5. Скористаємося формулою (4.3). Маємо
Задача№2 Середня кількість автобусів, що підходять на зупинку протягом години, дорівнює 4 (потік пуассонівський). Яка ймовірність, що людина, що прийшла на зупинку, буде чекати автобуса більше 10 хв? Розв’язання Спочатку знайдемо ймовірність протилежної події, що чекати автобуса доведеться не більше 10 хв. Таким чином, за умовою l =4, t = 1/6, k = 1. Скористаємося формулою (4.3). Маємо
Тому шукана ймовірність дорівнює:
Задача№3 Середнє число катерів, що підходять до річкового причалу протягом години дорівнює 5 (потік пуассонівський). Знайти ймовірність події, що за півгодини підійде до причалу 3 катери.
Розв’язання Скористаємось формулою (4.3). За умовою l =5, t = 1/2, k = 3. Маємо
Задача№4
У міське довідкове бюро кожної хвилини надходять 4 телефонні дзвінки. Яка ймовірність, що протягом 2 хв телефон буде мовчати?
Розв’язання Скористаємось формулою (4.3). За умовою l =4, t = 2, k =0. Маємо
Практичне заняття 17 ЛАНЦЮГИ МАРКОВА Нехай здійснюється послідовність випробувань, у кожному з яких може настати одна і тільки одна з k попарно несумісних подій Означення. Послідовність випробувань (або послідовність випадкових величин X 1, X 2, …, Xn, …) утворює ланцюг Маркова, якщо ймовірність того, що при n -му випробуванні (n = 1, 2, …) настане певна подія Aj (j = 1, 2, …, k), залежить лише від того, яка подія настала при (n – 1)-му випробуванні і не залежить від результатів інших попередніх випробувань.
Згідно з означенням ланцюга Маркова при будь-яких n, i, j
P (Xn = j | Xn – 1 = i) =
Ланцюг Маркова називають однорідним, якщо умовні ймовірності Умовну ймовірність pij називають імовірністю переходу системи (за один крок) зі стану Ai в стан Aj; це є умовна ймовірність настання події Aj при деякому випробуванні за умови, що при попередньому випробуванні настала подія Ai. Ймовірності pij утворюють квадратну матрицю
яку називають матрицею переходу. Елементи матриці (5.2) задовольняють такі умови: 0 £ pij £ 1,
оскільки pij – ймовірності і система зі стану Ai обов’язково переходить до одного зі станів A 1, A 2, …, Ak. Для задання ланцюга Маркова, крім матриці переходу потрібно задати ще деякий початковий розподіл імовірностей, тобто ймовірності станів системи, що відповідають початку процесу – моменту t 0: pi (0) (pi (0) – ймовірність того, що в початковий момент t 0 система перебувала в стані Ai). При розгляді ланцюгів Маркова виникає таке питання: яка ймовірність того, що через n кроків система перейде зі стану Ai до Aj, або, інакше, яка ймовірність того, що при (s + n)-му випробуванні настане подія Aj, якщо при s -му випробуванні настала подія Ai? Позначимо цю ймовірність через pij (n). Якщо n > 1, m < n, то за формулою повної ймовірності
тобто
Якщо матрицю (pij (n)) Зокрема при m = 1 ця рівність дає P (n) = P · P (n – 1), звідки випливає, що P (n) = P n. При відомих імовірностях (5.4) станів системи у початковий момент t 0 легко знайти ймовірності pi (n) того, що система на n -му кроці буде в стані Ai
або в матричній формі
де
Послідовності переходу системи з одного стану в інший, коли зміна стану може відбуватись лише у заздалегідь фіксовані моменти часу t 0, t 1, t 2, …, tn, …, називаються простими ланцюгами Маркова з дискретним часом. Якщо зміна станів системи може відбуватися в будь-який момент часу t > t 0, то така послідовність зміни станів утворює простий ланцюг Маркова з неперервним часом. Всі результати, що мають місце для ланцюгів з дискретним часом, узагальнюються і для ланцюгів Маркова з неперервним часом.
Розв’язування задач Задача №1 Нехай { A 1, A 2, A 3} – множина можливих станів деякої системи. Відомі ймовірності pij переходу системи зі стану Ai до стану Aj за один крок: p 11 = 0,5; p 12 = p 13 = 0,25; p 21 = p 22 = 0,25; p 23 = 0,5; Знайти матрицю переходу P (2). Розв’язання Матриця переходу при заданих умовах має вигляд:
Знайдемо матрицю переходу за два кроки P (2), вона має вигляд:
Задача№2
В умовах попередньої задачі визначити: а) ймовірність того, що через два кроки система перебуватиме в стані A 1; б) ймовірність того, що через два кроки система перебуватиме в стані A 2; в) ймовірність того, що через два кроки система перебуватиме в стані A 3.
Розв’язання Якщо ймовірності станів A 1, A 2, A 3 системи у початковий момент мають значення p 1(0) = 0,5, p 2(0) = p 3(0) = 0,25, то ймовірність того, що через два кроки система перейде до стану A 1 обчислюється за формулою (5.6):
p 1(2) = 0,375·0,5 + 0,3125 · 0,25 + 0,3125 · 0,25 = 0,34375.
Аналогічно обчислюємо ймовірності переходу системи за два кроки p 2(2) = 0,25 · 0,5 + 0,25·0,25 + 0,25·0,25 = 0,25,
p 3(2) = 0,375 · 0,5 + 0,4375 · 0,25 + 0,4375 · 0,25 = 0,40625. Задача№3 Фізична система може знаходитись в одному зі станів A 1, A 2, A 3. Задані матриця переходу і початковий розподіл імовірностей:
Знайти: а) матрицю переходу P (2); б) ймовірність того, що через два кроки система перебуватиме в стані A 2.
Розв’язання
Знайдемо матрицю переходу за два кроки P (2), вона має вигляд:
Визначимо ймовірність того, що через два кроки система перебуватиме в стані A 2:
Задача№4 Кожний водій автопідприємства заправляє свою машину 1 раз на тиждень на одній з трьох автозаправок. На одному з тижнів було опитано 100 водіїв: 50 водіїв заправляються на І заправці, серед них 45 наступного тижня будуть заправлятись на І заправці, 4 – на ІІ і 1 – на ІІІ заправках; 20 водіїв заправляються на ІІ заправці, серед них 8 наступного тижня будуть заправлятись на І, 6 на ІІ і 6 на ІІІ заправках; 30 водіїв заправляються на ІІІ заправці, серед них 21 наступного тижня будуть заправлятись на І, 3 на ІІ і 6 на ІІІ заправках. Потрібно а) знайти матрицю перехідних ймовірностей Р; б) знайти кількість водіїв, що будуть заправлятись на кожній заправці через 2 тижні.
Розв’язання Знайдемо матрицю переходу і початковий розподіл ймовірностей:
p 1(0) = 50/100=0,5, p 2(0) = 20/100=0,2, p 3(0) = 30/100=0,3.
Знайдемо матрицю переходу за два кроки P (2), вона має вигляд:
Транспонуємо матрицю
Знайдемо
Отже, через два тижня 81 водій буде заправлятись на І заправці, 11 водіїв буде заправлятись на ІІ заправці і 8 водіїв буде заправлятись на ІІІ заправці. Задачі для аудиторної та самостійної роботи 1. Нехай
2. Для випадкового процесу з попередньої задачі знайти одновимірну щільність розподілу, математичне сподівання.
3. Для випадкового процесу
4. Для випадкового процесу
5. В умовах попередньої задачі знайти одновимірну та двовимірну функції розподілу випадкового процесу.
6. Для випадкового процесу
7. Для цілочисельного випадкового процесу
8. Розглядається випадковий процес
9. Випадковий процес
10. Для випадкового процесу
11. Задані характеристики випадкового процесу 12. Для випадкового процесу
13. Випадковий процес X (t) заданий одновимірною щільністю розподілу
Знайти математичне сподівання mx (t), дисперсію Dx (t) і середнє квадратичне відхилення s x (t) випадкового процесу X (t). 14. Задані характеристики випадкового процесу X (t): mx (t) = 2 t + 5, Kx (t 1, t 2) = 3 t 1 + 4 t 2. Знайти характеристики випадкового процесу Y (t) = 2 t X (t) – 4. 15. Задані характеристики випадкового процесу X (t): mx (t) = 3 t 2 – 8 t + 1, 16. Знайти характеристики випадкової гармоніки X (t) = A cos (w t + F), де A і w – невипадкові амплітуда і частота, F – випадкова початкова фаза, розподілена рівномірно на відрізку [0, 2p]. 17. Довести, що випадковий процес X (t) = Y sin w t + Z cos w t, де Y, Z – некорельовані випадкові величини з характеристиками my = mz = 0, Dy = Dz = D, w – невипадкова величина, є стаціонарним. 18. Кореляційна функція kx (t) стаціонарного випадкового процесу має вигляд kx (t) = e –2| t |. Знайти спектральну щільність Sx (w). 19. Спектральна щільність стаціонарного випадкового процесу задана у вигляді
Знайти кореляційну функцію. 20. Випадковий процес X (t) має вигляд X (t) = 3 t Y + 4, де Y – випадкова величина, розподілена за показниковим законом з параметром l. Знайти математичне сподівання mx (t) і дисперсію Dx (t) випадкового процесу X (t). 21. Відомі характеристики випадкового процесу X (t): mx (t) = 5, 22. Випадковий процес X (t) має характеристики mx (t) = t 2 – 3 t + 4, 23. Випадковий процес X (t) має характеристики mx (t) = 6 t – 4,
24 Фізична система може знаходитись в одному зі станів A 1, A 2, A 3. Задані матриця переходу і початковий розподіл імовірностей
Знайти: а) матрицю переходу P (2); б) ймовірність того, що через два кроки система перебуватиме в стані A 2.
Відповіді 1. 3. 5. 6. 7. 8. 9. 10. 11. 12.
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.118.28 (0.008 с.) |

 .
. , k = 0, 1, 2, … (4.3)
, k = 0, 1, 2, … (4.3) .
. .
.
 .
. .
. . (5.1)
. (5.1) . Надалі будуть розглядатися лише однорідні ланцюги Маркова.
. Надалі будуть розглядатися лише однорідні ланцюги Маркова. , (5.2)
, (5.2) (i = 1, 2, …, k), (5.3)
(i = 1, 2, …, k), (5.3) (5.4)
(5.4) ,
, . (5.5)
. (5.5) позначити через P (n) (при цьому P (1) = P), то рівність (5.5), згідно з відомим з алгебри правилом множення матриць, означає, що коли 0 < m < n, то P (n) = P (m)· P (n – m).
позначити через P (n) (при цьому P (1) = P), то рівність (5.5), згідно з відомим з алгебри правилом множення матриць, означає, що коли 0 < m < n, то P (n) = P (m)· P (n – m). :
: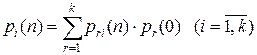 , (5.6)
, (5.6) , (5.7)
, (5.7) ,
, – транспонована відносно P (n) матриця.
– транспонована відносно P (n) матриця. .
.
 , p 1(0) = 1, p 2(0) = p 3(0) = 0.
, p 1(0) = 1, p 2(0) = p 3(0) = 0.


 ,
,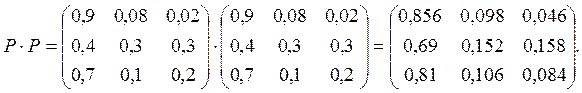 За формулою
За формулою 
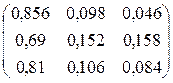 ,
, 
 :
:
 :
:


 рівномірно розподілена випадкова величина на відрізку
рівномірно розподілена випадкова величина на відрізку  . Знайти одновимірну функцію розподілу випадкового процесу
. Знайти одновимірну функцію розподілу випадкового процесу  , де
, де  .
. , де
, де  , знайти одновимірну функцію розподілу, (
, знайти одновимірну функцію розподілу, ( ), одновимірну щільність розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення.
), одновимірну щільність розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення. задана двовимірна щільність розподілу
задана двовимірна щільність розподілу  при
при  і 0 в інших випадках
і 0 в інших випадках  . Знайти одновимірну щільність розподілу, математичне сподівання, дисперсію, кореляційну функцію. Чи буде такий процес стаціонарним? Яку невипадкову функцію потрібно додати до процесу
. Знайти одновимірну щільність розподілу, математичне сподівання, дисперсію, кореляційну функцію. Чи буде такий процес стаціонарним? Яку невипадкову функцію потрібно додати до процесу 
 при
при 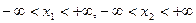 . Знайти одновимірну та двовимірну щільності функції розподілу.
. Знайти одновимірну та двовимірну щільності функції розподілу. , знайти математичне сподівання, дисперсію.
, знайти математичне сподівання, дисперсію. , де для
, де для 
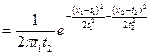 . Знайти числові характеристики цього процесу. Чи буде такий процес стаціонарним? ергодичним?
. Знайти числові характеристики цього процесу. Чи буде такий процес стаціонарним? ергодичним?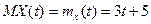 ,
, 
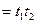 . Знайти відповідні характеристики процесу
. Знайти відповідні характеристики процесу  . Чи буде такий процес стаціонарним? ергодичним?
. Чи буде такий процес стаціонарним? ергодичним? і встановити його стаціонарність.
і встановити його стаціонарність. ,
,  . Знайти характеристики випадкового процесу
. Знайти характеристики випадкового процесу  .
. , де
, де  – незалежні випадкові величини з відомими математичним сподіванням і дисперсією:
– незалежні випадкові величини з відомими математичним сподіванням і дисперсією: 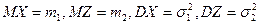 . Знайти відповідні числові характеристики і кореляційну функцію. Чи буде такий процес стаціонарним?
. Знайти відповідні числові характеристики і кореляційну функцію. Чи буде такий процес стаціонарним? .
.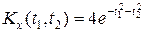 . Знайти характеристики випадкового процесу Y (t) = t 2 X (t) + 3.
. Знайти характеристики випадкового процесу Y (t) = t 2 X (t) + 3. .
. . Знайти характеристики випадкового процесу Y (t) = 5 X (t) – 7.
. Знайти характеристики випадкового процесу Y (t) = 5 X (t) – 7. . Знайти характеристики випадкового процесу
. Знайти характеристики випадкового процесу  .
. .
. , p 1(0) = 1, p 2(0) = p 3(0) = 0.
, p 1(0) = 1, p 2(0) = p 3(0) = 0. . 2.
. 2.  ;
;  .
. ;
;  ;
;  ;
;  4.
4.  ;
; 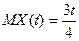 ;
;  ;
;  ; не буде стаціонарним; додати невипадкову функцію
; не буде стаціонарним; додати невипадкову функцію  .
.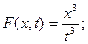
 .
. .
. .
. ; процес стаціонарний та ергодичний.
; процес стаціонарний та ергодичний. ;
;  ; процес стаціонарний.
; процес стаціонарний.
 ; процес стаціонарний.
; процес стаціонарний. .
.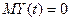 ;
;  ;
; 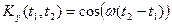 ; процес стаціонарний.
; процес стаціонарний.


