
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система двох випадкових величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Тут (xi, yj) – можливі пари значень випадкових величин Х та Y Оскільки події (X = xi, Y = yj)
Закони розподілу кожної із складових Х та Y визначаються так:
Функцією розподілу (або інтегральною функцією розподілу) двовимірної випадкової величини (Х, Y) називається функція F (x, y) = P (X < x, Y < y), яка визначає для кожної пари чисел х, у ймовірність того, що випадкова величини Х прийме значення, менше від х, і при цьому випадкова величини Y прийме значення, менше від у. Інтегральна функція розподілу F (x, y) має такі властивості. 1. Значення функції F (x, y) задовольняють умову 0 £ F (x, y) £ 1. 2. F (x, y) є неспадною функцією по кожному з аргументів. 3. Виконуються такі граничні співвідношення:
Дійсно, очевидно, що (рис. 5, а) P (a £ X < b, Y < y) = P (X < b, Y < y) – P (x < a, Y < y) = F (b, y) – F (a, y). Аналогічно (рис. 5, б) P (X < x, c £ Y £ d) = P (X < x, Y < d) – P (X < x, Y < c) = F (x, d) – F (x, c). Нарешті (рис. 5, в)
Для задання неперервної двовимірної випадкової величини крім інтегральної функції розподілу F (x, y) використовують і диференціальну функцію розподілу (щільність розподілу) f (x, y) двовимірної випадкової величини (Х, Y). Якщо F (x, y) неперервна, диференційовна по кожному із своїх аргументів і для неї існує мішана похідна другого порядку
Для неї виконується умова
Інтегральна функція розподілу F (x, y) системи (Х, Y) виражається через щільність розподілу f (x, y)так:
Ймовірність потрапляння випадкової точки (X, Y) в область D площини XOY (подія (X, Y)Î D) обчислюється за формулою
Щільності розподілу складових X та Y системи (Х, Y) виражаються через щільність розподілу системи за формулами
Умовним законом розподілу однієї з випадкових величин, що входять в систему (Х, Y), називається закон розподілу цієї величини, який одержується при умові, що інша випадкова величина прийняла певне значення. Якщо Х та Y – неперервні випадкові величини, то умовні щільності розподілу ймовірностей Х та Y виражаються через безумовні за формулами
Випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, яке можливе значення прийняла інша величина.Для незалежних випадкових величин Х та Y виконуються умови F (x, y) = F 1(x)· F 2(y), f (x, y) = f 1(x)· f 2(y). Основними числовими характеристиками системи випадкових величин (Х, Y) є наступні. 1. Математичні сподівання складових М (Х) та М (Y) - координати центра розсіювання системи. Формули для обчислення М (Х) і М (Y) мають такий вигляд: для системи дискретних випадкових величин
для системи неперервних випадкових величин
2. Дисперсії D (X) і D (Y), що характеризують розсіювання випадкової точки (Х; Y) уздовж осей Ох та Оу відповідно. Формули для обчислення D (X) і D (Y) мають вигляд: для системи дискретних випадкових величин
для системи неперервних випадкових величин
3. Середні квадратичні відхилення s(Х) та s(Y) складових Х та Y
4. Кореляційний момент m xy = M [(X – M (X))(Y – M (Y))] випадкових величин Х та Y, який характеризує зв”язок між ними. Формули, за якими обчислюють m xy, мають вигляд: для системи дискретних випадкових величин
для системи неперервних випадкових величин
Для незалежних випадкових величин кореляційний момент дорівнює нулю. 5. Коефіцієнт кореляції випадкових величин
який є мірою лінійної залежності між випадковими величинами Х і Y. Якщо випадкові величини Х і Y незалежні, то rxy=0, якщо вони зв”язані лінійною залежністю, то Залежність між двома випадковими величинами, за якої при зміні однієї з величин змінюється середнє значення другої, називається кореляційною залежністю. Кореляційну залежність між випадковими величинами Х і Y описують функції регресії
де М (Y|х) - умовне математичне сподівання випадкової величини Y при Х = х; М (Х|y) – умовне математичне сподівання випадкової величини Х при Y = y. Якщо обидві функції регресії лінійні, має місце лінійна кореляційна залежність між випадковими величинами Х і Y. Рівняння прямих регресії записуються так:
(тут mx = M (X), my = M (Y), Система двох випадкових величин (X, Y) має рівномірний розподіл в області D площини XOY, якщо щільність розподілу системи має вигляд
де SD – площа області D. При цьому ймовірність потрапляння випадкової точки в частину G області D (G Ì D) визначається за формулою
де SG – площа області G. Двовимірна випадкова величина (Х, Y) називається розподіленою за нормальним законом, якщо її щільність розподілу ймовірностей має вигляд
Тут a 1= mx, a 2= my, s1=s x, s2=s y, r=rxy – параметри нормального розподілу. Щільності розподілу випадкових величин Х та Y мають вигляд
тобто складові Х та Y розподілені за нормальним законом. У випадку нормального закону розподілу системи (X,Y) обидві функції регресії лінійні, тому складові Х та Y зв’язані лінійною кореляційною залежністю. Якщо випадкові величини Х та Y некорельовані (r = 0), має місце залежність f (x, y) = f 1(x) f 2(y), тобто Х і Y – незалежні. При цьому ймовірність потрапляння випадкової точки (X, Y) в прямокутник D з вершинами (a, g), (a, d), (b, g), (b, d), де a < b, g < d, обчислюється за формулою
(8.19) Тут
Опитування з теорії
1. Дати означення двовимірної випадкової величини і з¢ясувати її геометричний зміст. Які бувають системи випадкових величин? 2. Як задається дискретна двовимірна випадкова величина? 3. Дати означення функції розподілу двовимірної випадкової величини. Які властивості має ця функція? 4. Дати означення щільності розподілу неперервної двовимірної випадкової величини. Які властивості має ця функція? 5. Як виражаються щільності розподілу складових Х, Y системи (X,Y) через щільність розподілу двовимірної випадкової величини (X,Y)? 6. Дати означення незалежних випадкових величин. Вказати умови незалежності двох випадкових величин. 7. Записати формули для обчислення математичних сподівань складових Х та Y:а) у випадку системи (X,Y) дискретних випадкових величин; б) у випадку системи (X,Y) неперервних випадкових величин. 8. Записати формули для обчислення дисперсій складових Х та Y: а) у випадку системи (X,Y) дискретних випадкових величин; б) у випадку системи (X,Y) неперервних випадкових величин. 9. Дати означення кореляційного моменту двох випадкових величин і навести формули його обчислення. 10. Дати означення коефіцієнта кореляції двох випадкових величин. Які властивості має коефіцієнт кореляції? 11. Яку залежність між двома випадковими величинами описують функції регресії? Записати рівняння прямих регресії. 12. Дати означення двовимірної випадкової величини (X,Y), рівномірно розподіленої в деякій області D площини. Як обчислюється ймо- вірність потрапляння випадкової точки (X,Y) в частину області D? 13. Дати означення двовимірної випадкової величини (X,Y), розподіленої за нормальним законом. Перерахувати основні властивості нормального розподілу на площині.
Задача 1. Для двовимірної дискретної випадкової величини (X, Y), заданої законом розподілу
знайти: 1) закони розподілу складових Х та Y; 2) умовний закон розподілу складової Х при умові, що складова Y прийняла значення у 1 і умовний закон розподілу складової Y при умові, що складова Х прийняла значення х 2; 3) M (X), M (Y), D (X), D (Y), s(X), s(Y), m xy, rxy; 4) рівняння прямих регресії Y на Х та X на Y. Розв”язання. 1) Ймовірності можливих значень випадкових величин Х та Y обчислюємо за формулами (8.1) p (x 1) = 0,25 + 0,15 + 0,32 = 0,72; p (x 2) = 0,1 + 0,05 + 0,13 = 0,28; p (y 1) = 0,25 + 0,1 = 0,35; p (y 2) = 0,15 + 0,05 = 0,2; p (y 3) = 0,32 + 0,13 = 0,45. Отже, закони розподілу складових Х та Y мають вигляд
2) Знаходимо умовні ймовірності можливих значень Х при умові, що складова Y прийняла значення y 1=10:
Отже, умовний закон розподілу Х має вигляд
Аналогічно знаходимо умовний закон розподілу складової Y при умові Х = х 2:
3) Числові характеристики системи (Х, Y) та її складових знаходимо за формулами (8.7), (8.9), (8.11), (8.12), (8.14): M (X) = 3(0,25 + 0,15 + 0,32) + 6(0,1 + 0,05 + 0,13) =3,84; M (Y) = 10(0,25 + 0,1) + 14(0,15 + 0,05) + 18(0,32 + 0,13) = 14,4; D (X) = 32 (0,25 + 0,15 + 0,32) + 62 (0,1 + 0,05 + 0,13) – (3,84)2 = 1,8144; D (Y) = 102 (0,25 + 0,1) +142 (0,15 + 0,05) + 182 (0,32 + 0,13) – (14,4)2 = = 12,64;
m xy = 3 ×10 × 0,25 + 3 ·14 · 0,15 + 3 × 18 · 0,32 + 6 ×10 · 0,1 + 6 ×14 · 0,05 + + 6 ×18 · 0,13 – 3,84 ×14,4 = 0,024;
4) Рівняння прямих регресії записуємо, використовуючи їх загальний вигляд (8.15)
або
Задача 2. Задана інтегральна функція F (x, y) двовимірної випадкової величини (Х, Y)
Знайти: 1) щільність розподілу системи (Х, Y); 2) ймовірність попадання випадкової точки (Х, Y) в прямокутник 1 £ х £ 2, 3 £ у £ 5. Розв”язання. 1) Скористаємося формулою (8.3). Знаходимо частинні похідні
Отже, шукана щільність розподілу системи (Х, Y) має вигляд
2) Поклавши у формулі (8.2) a = 1, b = 2, c = 3, d = 5, дістанемо P (1 £ X £ 2, 3 £ Y £ 5) = F (2;5) – F (1;5) – F (2;3) + F (1;3) = = (1– 2-2 – 2-5 + 2-7) – (1– 2-1 – 2-5 + 2-6) – (1– 2-2 – 2-3 + 2-5) + + (1– 2-1 – 2-3 + 2-4) = 2-7 – 2-6 – 2-5 + 2-4 = 3/128. Задача 3. Задана диференціальна функція f (х, у) двовимірної випадкової величини (Х, Y)
Знайти: 1) коефіцієнт а; 2) інтегральну функцію F (х, у) системи (Х, Y); 3) щільності розподілу складових Х та Y; 4) математичні сподівання, дисперсії, середні квадратичні відхилення випадкових величин Х та Y, їх кореляційний момент та коефіцієнт кореляції.
Розв”язання. Коефіцієнт а знаходимо, виходячи з властивості (8.4) диференціальної функції розподілу системи (Х, Y). Маємо
Отже, а = 1/2. 2) Інтегральну функцію F (х, у) системи (Х, Y) знаходимо за формулою (8.5). Очевидно, що F (х, у)=0, якщо x <0 або y <0. Нехай
Якщо
Аналогічно встановлюємо, що F (x, y) =
3) Щільність розподілу f 1(x) складової Х системи (Х, Y) знаходимо за формулою (8.6)
і f 1(x) = 0 при х < 0 або х > p/2, тобто
Враховуючи симетрію функції f (x, y) відносно аргументів х та y, записуємо щільність розподілу f 2(y) складової Y системи (Х, Y)
4) За формулою (8.8) обчислюємо математичне сподівання випадкової величини Х.
Аналогічно, за формулою (8.10), застосувавши двічі інтегрування частинами, дістанемо
Тепер Знову враховуючи симетрію функції f (x, y) відносно аргументів х та y, дістанемо M (Y) = Кореляційний момент випадкових величин Х та Y обчислюємо за формулою (8.13)
Коефіцієнт кореляції випадкових величин Х та Y обчислюємо за формулою (8.14)
Задача 4. Задана диференціальна функція системи випадкових величин (Х, Y)
Знайти диференціальні функції розподілу складових f 1(x), f 2(y) та умовні диференціальні функції складових f (x ï y), f (y ï x). З’ясувати питання про залежність випадкових величин Х та Y. Розв”язання. Знайдемо диференціальну функцію складової Х. При x <0 f 1(x) = 0. Якщо х ³0, то
Аналогічно знаходимо
Оскільки f (x, y) = f 1(x) × f 2(y), то складові X, Y системи (Х, Y) незалежні і умовні диференціальні функції випадкових величин Х та Y дорівнюють їхнім безумовним диференціальним функціям f (x | y) = f 1(x), f (y | x) = f 2(y).
Задача 5. Двовимірна випадкова величина (Х, Y) розподілена рівномірно в прямокутнику D: – 1 < х < 2, 1 < у < 2. Знайти інтегральну та диференціальну функції розподілу системи (Х, Y) та обчислити ймовірність того, що випадкова точка (Х, Y) потрапить у другий квадрант площини ХОY. Розв”язання. Враховуючи, що площа прямокутника D дорівнює 3 кв.од., за формулою (8.16) знаходимо диференціальну функцію системи (Х, Y):
При побудові інтегральної функції системи скористаємося формулою (8.5) і тим, що інтеграл
дає площу прямокутника a £ х £ b, c £ у £ d. Якщо х £ -1 або y£ 1, F (x, y) = 0. Якщо (x; y)Î D, то
При –1 < х < 2, у ³ 2 маємо Аналогічно при 1 < у < 2, х ³ 2 дістанемо
Отже,
Шукану ймовірність обчислюємо за допомогою формули (8.17). Маємо P (X < 0, Y > 0)= P (–1 £ X < 0, 1 £ Y £ 2) = Задача 6. Двовимірна випадкова величина (Х, Y) розподілена за нормальним законом з параметрами a 1 = M (X) = 3, a 2 = M (Y) = -2, s1 = s(X) = 1, s2 = s(Y) = 4, r = 0. Записати вираз для щільності розподілу системи (Х, Y). Обчислити ймовірність потрапляння випадкової точки (Х, Y) в прямокутник D: 1 £ х £ 6, -3 £ у £ 4 площини ХОY. Розв”язання. Враховуючи значення парметрів нормального закону розподілу системи (Х, Y), за формулою (8.18) записуємо щільність розподілу
Потрібну ймовірність обчислюємо за формулою (8.19)
= (F(3) – F(–2))×(F(1,5) – F(–0,25)) = (F(3) + F(2))×(F(1,5) + +F(0,25)) = (0,49865 + 0,4772)×(0,4332 + 0,0987) = 0,5191.
Задачі для аудиторної і самостійної роботи 1. Для двовимірної дискретної випадкової величини (X, Y), заданої законом розподілу, знайти: 1) закони розподілу складових Х та Y; 2) умовний закон розподілу складової Х при умові, що складова Y прийняла значення у 1 і умовний закон розподілу складової Y при умові, що складова Х прийняла значення х 2; 3) M (X), M (Y), D (X), D (Y), s(X), s(Y), m xy, rxy; 4) рівняння прямих регресії Y на Х та X на Y.
Відповідь:
а) M (X) = 1,45; M (Y) = 3,2; D (X) = 4,15; D (Y) = 0,96; s(X) = 2,04; s(Y) = 0,98; m xy = 0,86; rxy =0,43; б) M (X)=1,65; M (Y)=5,1; D (X)=2,2275; D (Y)=1,09; s(X)=1,4925; s(Y) = 1,044; m xy = – 0,465; rxy = – 0,2984. 2. Задана інтегральна функція F (x, y) двовимірної випадкової величини (Х, Y). Знайти диференціальну функцію системи (Х, Y).
Відповідь: а)
3. Задана диференціальна функція f (х, у) системи випадкових величин (Х, Y). Знайти інтегральну функцію системи.
б) Відповідь: a) F (x, y) = 20[arctg (x /4)/(4p) + 0,125] [arctg (y /5)/(5p) + 0,1];
4. Задана диференціальна функція f (x, y) неперервної двовимірної випадкової величини (Х, Y). Знайти: 1) диференціальні функції складових Х та Y; 2) умовні диференціальні функції складових. З’ясувати, чи будуть залежними величини Х та Y.
Відповідь: а)
б) f (x | y) = f 1(x), f (y | x) = f 2(y); складові незалежні. 5. Задана диференціальна функція f (x, y) неперервної двовимірної випадкової величини (Х, Y). Знайти: а) математичні сподівання та дисперсії складових Х та Y; б) кореляційний момент системи (Х, Y) та коефіцієнт кореляції випадкових величин Х і Y.
Відповідь: 1) M (X) = M (Y) = 6. Двовимірна випадкова величина (Х, Y) розподілена за нормальним законом з параметрами mx = my = 0, s x = s y = s, rxy = 0. Обчислити ймовірності таких подій: а)| Y | < Х; б) Y < X; в) Y < | X |. Відповідь: a) 0,25; б) 0,5; в) 0,75. 7. Випадкова точка (Х, Y) розподілена за нормальним законом на площині Відповідь: 0,467. Практичне заняття 9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1058; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.209.215 (0.015 с.) |

 Дискретна двовимірна випадкова величина (Х, Y) може бути задана за допомогою таблиці
Дискретна двовимірна випадкова величина (Х, Y) може бути задана за допомогою таблиці pij – ймовірності того, що випадкова величина Х прийме значення xi і одночасно з цим випадкова величина Y прийме значення yj, тобто pij = P (X = xi, Y = yj).
pij – ймовірності того, що випадкова величина Х прийме значення xi і одночасно з цим випадкова величина Y прийме значення yj, тобто pij = P (X = xi, Y = yj). утворюють повну групу, то має місце рівність
утворюють повну групу, то має місце рівність .
.
 . (8.1)
. (8.1) .
. За допомогою інтегральної функції розподілу F (x, y) можна легко обчислювати ймовірність того, що в результаті випробування випадкова точка (X, Y)потрапить в одну з областей, зображених на рис. 5.
За допомогою інтегральної функції розподілу F (x, y) можна легко обчислювати ймовірність того, що в результаті випробування випадкова точка (X, Y)потрапить в одну з областей, зображених на рис. 5. .
.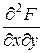 то щільність розподілу f (x, y) визначається рівністю
то щільність розподілу f (x, y) визначається рівністю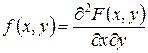 . (8.3)
. (8.3) . (8.4)
. (8.4) . (8.5)
. (8.5) .
. . (8.6)
. (8.6) .
. (8.7)
(8.7)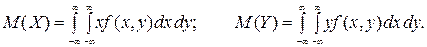 (8.8)
(8.8)
 (8.9)
(8.9)
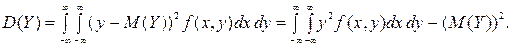 (8.10)
(8.10) . (8.11)
. (8.11) (8.12)
(8.12)
 . (8.13)
. (8.13) , (8.14)
, (8.14) =1. В загальному випадку
=1. В загальному випадку  .
. ,
, – пряма регресії Y на Х,
– пряма регресії Y на Х,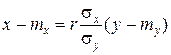 – пряма регресії Х на Y (8.15)
– пряма регресії Х на Y (8.15) , r = rxy).
, r = rxy). (8.16)
(8.16) (8.17)
(8.17) . (8.18)
. (8.18) ,
,
 – функція Лапласа.
– функція Лапласа. .
.


 .
. ,
, 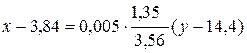
 – пряма регресії Y на Х,
– пряма регресії Y на Х, – пряма регресії Х на Y.
– пряма регресії Х на Y.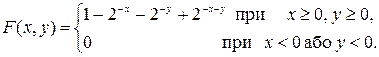
 .
.
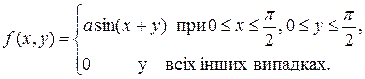
 або
або  . Але
. Але
 .
. . Тоді
. Тоді

 .
. , то
, то

 .
. при
при  і F (x, y) = 1 при
і F (x, y) = 1 при . Отже,
. Отже,
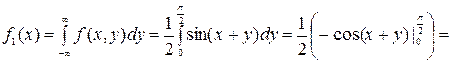
 , якщо 0 £ х £p/2,
, якщо 0 £ х £p/2,



 (використали інтегрування частинами).
(використали інтегрування частинами).
 .
. .
. , D (Y) =
, D (Y) =  , s(Y) =
, s(Y) =  .
.


 .
.


 . Отже,
. Отже,


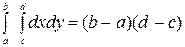
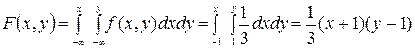 .
. .
. , а при х ³ 2, у ³ 2
, а при х ³ 2, у ³ 2 .
.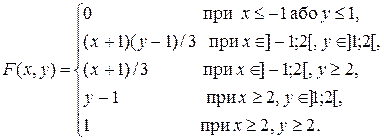
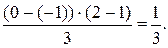
 .
.




 .
.


 .
.



 складові залежні.
складові залежні.
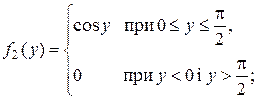


 ; D (X) = D (Y) = 1 – p/4; m xy = rxy = 0; 2) M (X) = M (Y) = (p + 4 –
; D (X) = D (Y) = 1 – p/4; m xy = rxy = 0; 2) M (X) = M (Y) = (p + 4 –  )/4; D (X) = D (Y) = [(p + 4)
)/4; D (X) = D (Y) = [(p + 4)  – 10]/2; m xy = rxy = 0.
– 10]/2; m xy = rxy = 0. . Знайти ймовірність того, що випадкова точка потрапить у квадрат зі стороною а = 2, діагоналі якого лежать на координатних осях.
. Знайти ймовірність того, що випадкова точка потрапить у квадрат зі стороною а = 2, діагоналі якого лежать на координатних осях.


