
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кореляційна функція випадкового процесуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для оцінки ступеня залежності (зв’язку) двох перерізів випадкового процесу вводять нову характеристику.
Кореляційною функцією випадкового процесу
Властивості кореляційної функції 1. Якщо відома двовимірна щільність розподілу f (x1, x2, t1, t2) випадкового процесу X(t), то
або
2. При рівності аргументів Kx (t, t) = Dx (t). (1.20) 3. Кореляційна функція симетрична відносно своїх аргументів: Kx (t 1, t 2) = Kx (t 2, t 1). (1.21) 4. Модуль кореляційної функції не перевищує добутку середніх квадратичних відхилень випадкового процесу, взятих у точках, що відповідають аргументам кореляційної функції: | Kx (t 1, t 2)| £ s x (t 1)s x (t 2). (1.22)
5. При додаванні до випадкового процесу X(t) невипадкової функції j(x) кореляційна функція не змінюється, тобто якщо Y(t) = X(t) + j(t), (1.23) то (t1, t2) = Kx(t1, t2). (1.24) 6. При множенні випадкового процесу X(t) на невипадкову функцію j(t), його кореляційна функція множиться на j(t1)j(t2), тобто якщо Y(t) = j(t)X(t), то Ky(t1, t2) = j(t1)j(t2)Kx(t1, t2). (1.25) Кореляційна функція Kx(t1, t2) випадкового процесу X(t) характеризує залежність між двома перерізами X(t1) та X(t2) випадкового процесу. Чим менший зв’язок між цими перерізами, тим менше значення кореляційної функції Kx(t1, t2). У багатьох випадках замість кореляційної функції Kx(t1, t2) розглядають нормовану кореляційну функцію rx(t1, t2), яка визначається так:
Властивості нормованої кореляційної функції rx(t1, t2): 1) rx(t, t) = 1; 2) rx(t1, t2) = rx(t2, t1); (1.27) 3) |rx(t1, t2)| £ 1. Наближене значення кореляційної функції випадкового процесу X(t) за результатами n незалежних спостережень обчислюється за формулою
де xi(t) (і=1,…,n)– реалізації випадкового процесу, t1, t2, …, tk, …tl – вибрані моменти часу. При розв’язанні деяких задач виникає необхідність з’ясувати питання про залежність двох різних випадкових процесів X(t) та Y(t). Для цього використовується так звана взаємна кореляційна функція. Означення. Взаємною кореляційною функцією двох випадкових процесів X(t) та Y(t) називається невипадкова функція Kxy(t1, t2) двох аргументів t1 і t2, яка при кожній парі значень t1 і t2 дорівнює кореляційному моменту відповідних перерізів випадкових процесів X(t) та Y(t) Kxy(t1, t2) = M[(X(t1) – mx(t1))(Y(t2) – my(t2))]. (1.29) Випадкові процеси X(t), Y(t) називаються некорельованими, якщо Kxy(t1, t2) = 0 при будь-яких значеннях аргументів t1 і t2. Інакше випадкові процеси X(t) та Y(t) називаються корельованими. Стаціонарні випадкові процеси Випадковий процес
Імовірнісні характеристики стаціонарного процесу не повинні залежати від часу.
Одновимірна щільність стаціонарного випадкового процесу не залежить від часу:
Математичне сподівання стаціонарного процесу дорівнює сталій:
Дисперсія стаціонарного процесу дорівнює сталій
Двовимірна щільність розподілу стаціонарного процесу буде залежати не від аргументів
Кореляційна функція стаціонарного процесу
(1.35)
Випадковий процес
Властивості кореляційної функції стаціонарного випадкового процесу
1. Дисперсія стаціонарного процесу дорівнює значенню кореляційної функції в початку координат:
2. Кореляційна функція стаціонарного процесу парна:
3. Модуль кореляційної функції стаціонарного процесу не перевищує його дисперсії:
Випадковий процес Суть ергодичної властивості випадкового процесу: одна реалізація достатньої протяжності може замінити при обробці всю множину реалізацій. Якщо стаціонарний випадковий процес X(t) має ергодичну властивість, то його характеристики mx і kx(t) наближено знаходяться за формулами
де x(t) – одна з реалізацій випадкового процесу X(t). Якщо у формулі (1.41) покласти t = 0, то враховуючи, що kx(0) = Dx, одержимо
Математично ергодична властивість стаціонарного процесу записується так:
Якщо виконується рівність (1.43), то стаціонарний випадковий процес називається ергодичним щодо математичного сподівання; якщо ж має місце рівність (1.44), то процес є ергодичним відносно кореляційної функції. Необхідною і достатньою умовою ергодичності випадкового процесу щодо математичного сподівання є співвідношення
а щодо кореляційної функції – співвідношення
Достатня умова ергодичності випадкового процесу:
Контрольні запитання 1. Що називається випадковою функцією? Випадковим процесом? 2. Дати означення реалізації випадкової функції, випадкового процесу. 3. Яка випадкова величина називається перерізом випадкового процесу? 4. Дати означення одновимірного закону розподілу та одновимірної щільності розподілу випадкового процесу. 5. Які ще закони розподілу використовуються для вивчення випадкового процесу? 6. Які випадкові процеси називаються процесами з дискретним часом? Неперервним часом? 7. Як шукається математичне сподівання, дисперсія та середнє квадратичне відхилення випадкового процесу? 8. Як за наявності п реалізацій випадкового процесу наближено обчислюються його характеристики в певний момент часу? 9. Які випадкові процеси називаються стаціонарними у вузькому розумінні? в широкому розумінні? 10. Чому дорівнюють математичне сподівання та дисперсія стаціонарного процесу? Розв’язування задач
Задача №1
Нехай
Розв’язання Знайдемоодновимірну функцію розподілу випадкового процесу:
Тут
Підставимо у функцію
Отримаємо
Оскільки ця функція змінюється від 0 до 1, то
Підставимо замість
Ми отримали, що при кожному
Задача №2
Для випадкового процесу з попередньої задачі знайти одновимірну щільність розподілу, математичне сподівання.
Розв’язання Знайдемо одновимірну щільність розподілу випадкового процесу
Тепер визначимо математичне сподівання:
Задача №3 Випадковий процес X (t) заданий одновимірною щільністю розподілу
Знайти математичне сподівання mx (t), дисперсію Dx (t) і середнє квадратичне відхилення s x (t) випадкового процесу X (t).
Розв’язання
Розглянемо переріз випадкового процесу, що відповідає значенню t = t 0. X (t 0) – це випадкова величина, розподілена за нормальним законом зі щільністю розподілу
Параметри цього розподілу M (X (t 0)) = t 0, D (X (t 0)) = 4, s(X (t 0)) = 2. Тому згідно з означенням характеристиками заданого випадкового процесу X (t) будуть mx (t) = t, Dx (t) = 4, s x (t) = 2.
Задача №4 Для випадкового процесу
Розв’язання
при
При кожному
Щільність розподілу визначається так:
Знайдемо числові характеристики випадкового процесу.
Задача №5
Двовимірна щільність розподілу випадкового процесу X (t) має вигляд:
Знайти mx (t), Dx (t), Kx (t 1, t 2).
Розв’язання Оскільки
то випадкові величини X (t 1) і X (t 2) некорельовані, тому Kx (t 1, t 2) = 0, якщо t 1 ¹ t 2. Крім того, mx (t) = 0, Dx (t) = 1. Отже,
Задача №6
Для випадкового процесу
Розв’язання
Оскільки
то перерізи випадкового процесу є некорельовані випадкові величини і
Оскільки
то
є одновимірною щільністю розподілу. Знайдемо числові характеристики випадкового процесу.
Розглянутий процес не буде стаціонарним, оскільки його математичне сподівання є функцією часу, а не сталою величиною.
Задача №7
В умовах попередньої задачі знайти одновимірну та двовимірну функції розподілу випадкового процесу.
Розв’язання За означенням двовимірна функція розподілу визначається як подвійний інтеграл від двовимірної щільності:
де
Таким чином,
Одновимірна щільність, очевидно, має вигляд:
Задача №8 Задані характеристики випадкового процесу X (t): mx (t) = 2 t 2 – 3 t, Знайти характеристики випадкового процесу:
Розв’язання Знаходимо математичне сподівання my (t):
Кореляційну функцію Ky (t 1, t 2) випадкового процесу Y (t) знаходимо, використовуючи властивості 5, 6:
За властивістю 2 кореляційної функції маємо
Задача №9
Випадковий процес заданий двовимірною щільністю розподілу
Розв’язання Оскільки
то одновимірна щільність розподілу
Знайдемо одновимірну функцію розподілу:
Аналогічно, двовимірна функція розподілу дорівнює подвійному інтегралу по змінних
Задача №10
Для випадкового процесу з попередньої задачі знайти математичне сподівання, дисперсію, кореляційну функцію. Чи буде такий процес стаціонарним?
Розв’язання Знайдемо числові характеристики випадкового процесу. Спочатку визначимо математичне сподівання:
Далі визначаємо дисперсію і середнє квадратичне відхилення:
Оскільки перерізи випадкового процесу є некорельовані випадкові величини, то
і
Розглянутий процес не буде стаціонарним, оскільки його математичне сподівання є функцією часу, а не сталою величиною.
Задача №11
Розглядається випадковий процес
Розв’язання
Визначимо числові характеристики процесу
Тепер визначимо кореляційну функцію:
і
Процес є стаціонарним, оскільки математичне сподівання і кореляційна функція не залежать від часу. Процес є ергодичним за достатньою умовою ергодичності випадкового процесу, тобто
Задача №12
Випадковий процес Розв’язання
Знайдемо математичне сподівання:
Використовуючи властивості кореляційної функції, знайдемо:
Процес є стаціонарним, оскільки математичне сподівання і кореляційна функція не залежать від часу.
Задача №13
Для випадкового процесу
Розв’язання Знайдемо математичне сподівання:
Тепер визначимо дисперсію:
Визначаємо кореляційну функцію:
Процес стаціонарний, оскільки математичне сподівання є сталим і кореляційна функція не залежить від аргументів
Задача №14
Для випадкового процесу
Розв’язання Знайдемо математичне сподівання випадкового процесу
Далі визначаємо дисперсію заданого процесу
Тепер знаходимо кореляційну функцію:
Оскільки математичне сподівання є сталим, а кореляційна функція залежить від різниці аргументів
Задача №15
Відомі математичне сподівання та кореляційна функція випадкового процесу
Розв’язання Визначаємо математичне сподівання даного процесу:
Тепер знайдемо кореляційну функцію процесу
Дисперсію визначимо з останньої формули, приймаючи
Процес не буде стаціонарним, оскільки його кореляційна функція залежить не тільки від різниці, а і від суми аргументів Практичне заняття 14
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.92.213 (0.008 с.) |

 називається невипадкова функція Kx (t 1, t 2) двох аргументів
називається невипадкова функція Kx (t 1, t 2) двох аргументів 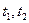 , яка при кожній парі значень
, яка при кожній парі значень 
 . (1.17)
. (1.17) , (1.18)
, (1.18) . (1.19)
. (1.19) кореляційна функція дорівнює дисперсії випадкового процесу:
кореляційна функція дорівнює дисперсії випадкового процесу: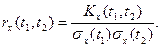 (1.26)
(1.26)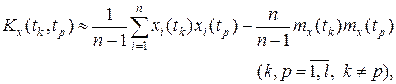 (1.28)
(1.28) :
: . (1.30)
. (1.30) . (1.31)
. (1.31)
 . (1.32)
. (1.32)
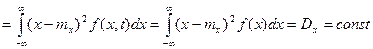 . (1.33)
. (1.33) і
і 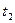 , а лише від їх різниці:
, а лише від їх різниці:

 . (1.34)
. (1.34)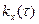 залежить від різниці аргументів
залежить від різниці аргументів 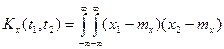

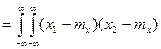
 .
. ,
, 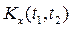
 . (1.36)
. (1.36) . (1.37)
. (1.37) . (1.38)
. (1.38) . (1.39)
. (1.39) (1.40)
(1.40) (1.41)
(1.41) (1.42)
(1.42)
 (1.43)
(1.43) (1.44)
(1.44)

 (1.46)
(1.46) (1.47)
(1.47) рівномірно розподілена випадкова величина на відрізку
рівномірно розподілена випадкова величина на відрізку  . Знайти одновимірну функцію розподілу випадкового процесу
. Знайти одновимірну функцію розподілу випадкового процесу  , де
, де  .
.
 .
. – функція рівномірного розподілу. Як відомо,
– функція рівномірного розподілу. Як відомо,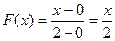 .
. .
.
 .
.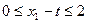 і
і  .
.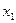 змінну
змінну  . Тоді
. Тоді .
. переріз випадкового процесу має рівномірний розподіл.
переріз випадкового процесу має рівномірний розподіл.
 .
. .
. .
. .
. , де
, де  . Знайти одновимірну функцію розподілу(
. Знайти одновимірну функцію розподілу( ), одновимірну щільність розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення.
), одновимірну щільність розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення.

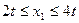 .
. .
.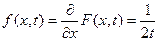 .
.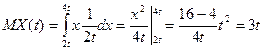 .
. .
.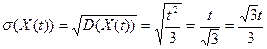 .
.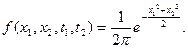

 при
при  і 0 в інших випадках. Знайти одновимірну щільність розподілу, математичне сподівання, дисперсію, кореляційну функцію. Чи буде такий процес стаціонарним?
і 0 в інших випадках. Знайти одновимірну щільність розподілу, математичне сподівання, дисперсію, кореляційну функцію. Чи буде такий процес стаціонарним? ,
, .
. ,
,
 ;
;
 ;
; .
.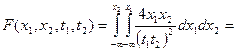
 ,
,
 .
. .
. .
.

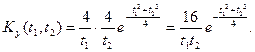


 при
при 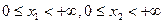 і 0 в інших випадках. Знайти одновимірну та двовимірну функції розподілу.
і 0 в інших випадках. Знайти одновимірну та двовимірну функції розподілу.

 ,
, .
. .
. :
: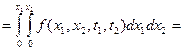
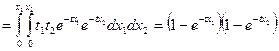 .
.
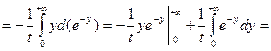
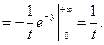
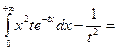


 ,
, .
. .
.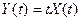 , де
, де  ;
; ;
; .
.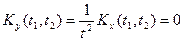 де
де 
 (див. попередню задачу)
(див. попередню задачу) .
. , де
, де 

 ,
, 
 . Чи буде такий процес стаціонарним?
. Чи буде такий процес стаціонарним?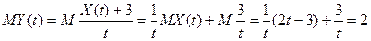 .
. .
.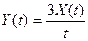 і встановити його стаціонарність.
і встановити його стаціонарність. .
. .
. .
. , де
, де  – незалежні випадкові величини з відомими математичним сподіванням і дисперсією:
– незалежні випадкові величини з відомими математичним сподіванням і дисперсією: 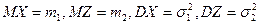 . Знайти відповідні числові характеристики і кореляційну функцію. Чи буде такий процес стаціонарним?
. Знайти відповідні числові характеристики і кореляційну функцію. Чи буде такий процес стаціонарним? :
: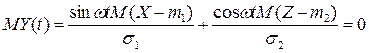 .
.





 .
.
 . Знайти числові характеристики і кореляційну функцію випадкового процесу
. Знайти числові характеристики і кореляційну функцію випадкового процесу  . Чи буде такий процес стаціонарним?
. Чи буде такий процес стаціонарним?
 .
.

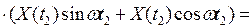

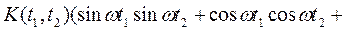
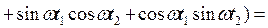
 ;
; .
. :
: .
.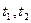 .
.


